isp算法学习-demosaicking
1800 Words|Read in about 9 Min|本文总阅读量次
本文是isp算法学习的第十一篇章,主要是讲述去马赛克。
01CMOS成像基础
Q:RAW图颜色相关问题,有人说RAW图是没有颜色灰度图,有人说RAW图是绿色的
A:其实上面说法不完全对。
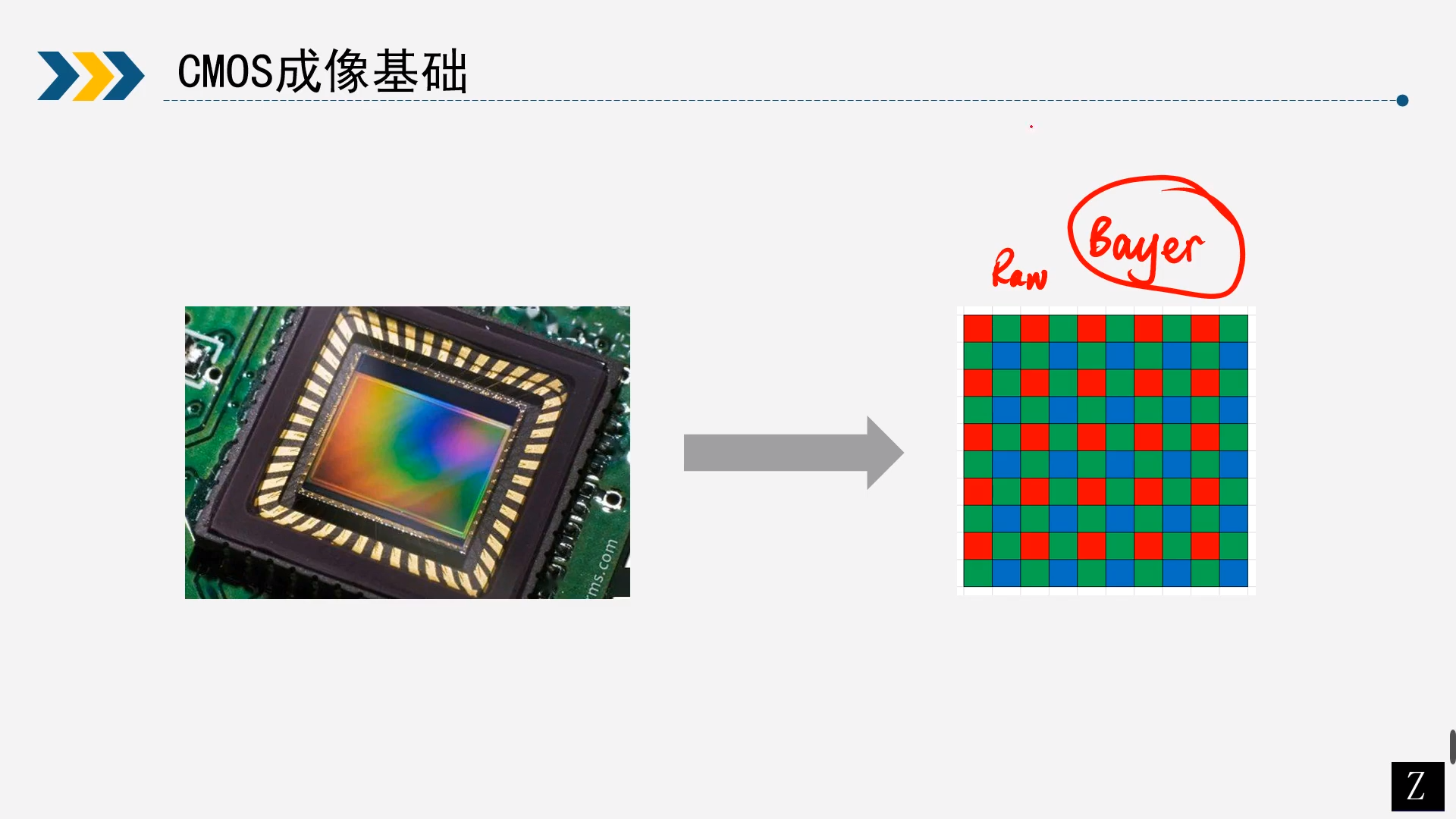
A:RGB图像实际上是3种颜色的叠加,但是RAW图每个像素只有一个颜色,RAW图是一维的,当只有一个通道的时候,那就是灰度图,灰度图没有颜色可言。
A:因为CFA(Color Filter Array,色彩滤波阵列/滤色阵列)的存在,加了一个颜色滤镜,所以看起来是有颜色,因为绿色占比多所以看起来就是绿色的。
A:光经过CMOS变成电信号,电信号加了增益之后,通过AD转换,变成数字信号,反应到RAW图上的数据本质也是电压的大小。因此,讨论RAW图的颜色没有意义,只能看到的是当前点对应通道分量的大小。
关于RAW补充几点
1)raw数据
raw 数据是 sensor 输出的原始数据,常用的一般有raw8, raw10, raw12等,分别表示一个像素点有 8bit、10bit、12bit 数据。
sensor 将光信号转化为电信号时的电平高低的原始记录,单纯地没有进行任何处理的图像数据,即表现的是 sensor 和镜头本征特性的数据。raw 数据在输出的时候是有一定顺序的,主要有四种: GRBG、RGGB、BGGR、GBRG。
2)raw 分哪几种格式
raw 一般分为 plain raw 和 mipi raw,主要是存储方式上的区别。
Plain raw
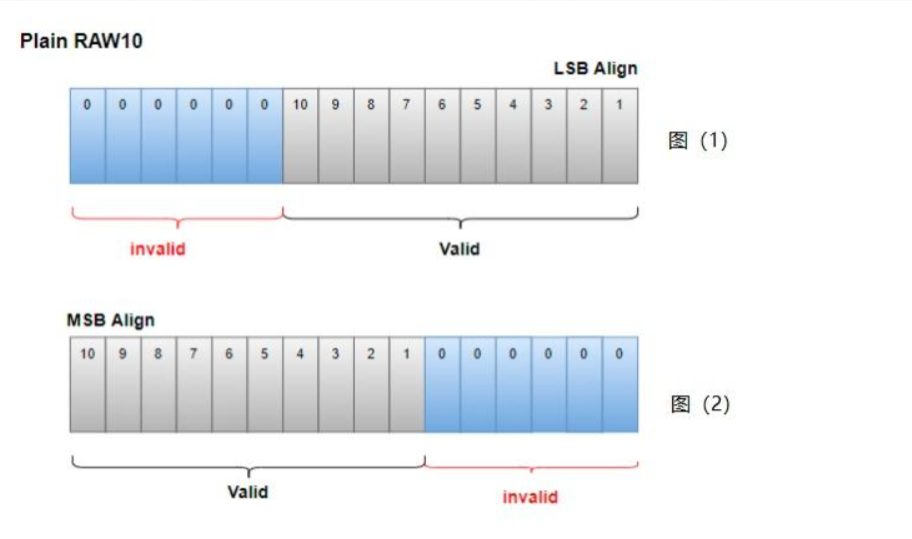
如下图所示是 Plain raw10 的示意图。
10bit的raw,单个像素也就是10bit,需要两个字节(16bit)来存储,那就会空出 6位用不到。
因为有空余,这里就涉及到一个高位/低位对齐的问题,也就是存储数据时,右移6位低位对齐(如上图1所示),左移6位高位对齐(如上图2所示)。关于高低位对齐,这个主要看平台厂商对数据处理有什么要求。
mipi raw
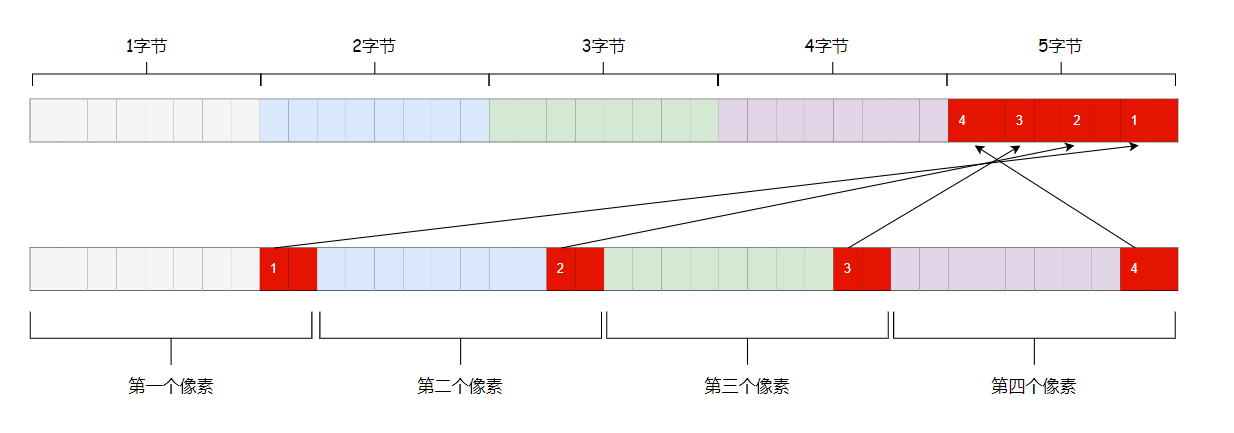
如下图所示是 mipi raw10 的示意图,以大端存储方式为例,它是把4个像素放到5个字节(40bit)中,组成一个包去存储。
前4字节依次存放 raw10 图像的前 4个像素的后 8位,4个像素的前 2位依次存放在包的第 5个字节中。
所以从存储方式来看,mipi raw 的存储方式是要比 plain raw 更节省内存。
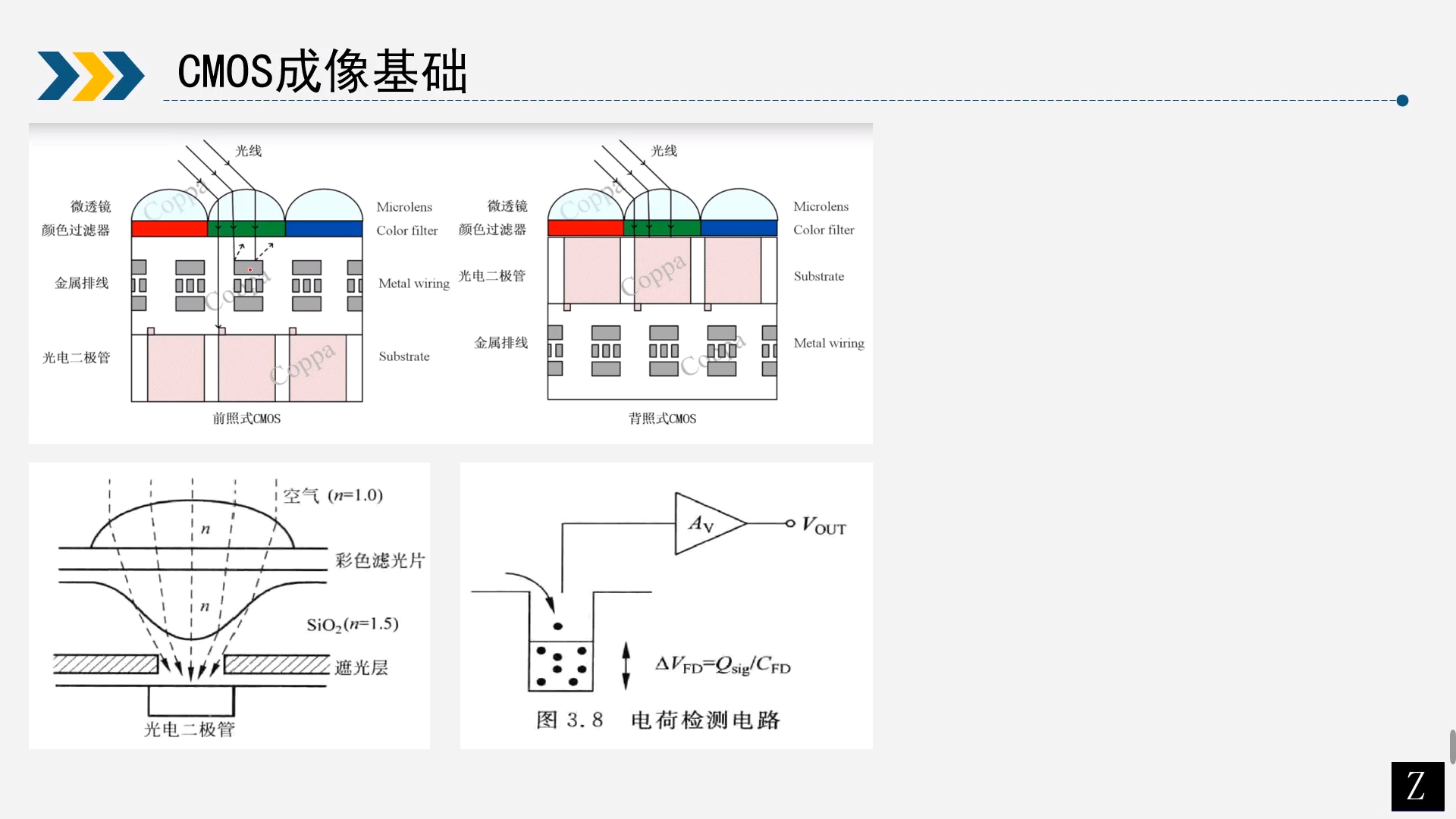
上面是CMOS大概的示意图。分为前照式CMOS和背照式CMOS。
前背照式主要区别是工艺问题,把金属排线放到前面就是前照式,放到和后面就是背照式。前照式缺点会挡住一部分从Lens过来的光,感光能力没有背照式强。背照式感光能力强,但是工艺较复杂。
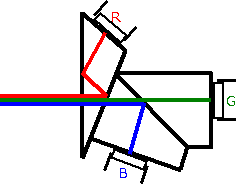
CMOS上光直接照射在微透镜上,能够尽可能的把光打在光电器件上,目的使光电转换效率最高。透镜下面是CFA,是一个色彩滤波阵列,分理处波长为红蓝绿三通道的颜色。在下面就是光电转换,因为光有波粒二象性,可以简单认为在某一个像素点上的光粒子数量,在电荷检测电路中会被检测到更多的电荷,经过一个放大器AV之后,那么表现为输出电压,电荷越大电压就越大。
人眼之所以有能感受到自然界的颜色,是因为人眼的感光细胞中有三种锥体细胞对红绿蓝三种颜色敏感,所以我们就可以通过RGB三种颜色来表示一个颜色空间,通过这个颜色空间中的点就能表示自然界中所有的颜色。那么数码相机只要能类似人一样获取自然界中的这三个分量,那么就能复现人眼看到的颜色。相机系统用的感光器件只是一个光电转换器件,所以感光器件只对亮度分量敏感,无法感知颜色,所以需要通过滤光片将光线分解成RGB三个分量然后再用感光期间去接受。那么最直接的方式就是用三个滤光片分别过滤出RGB三个通道的分量,然后用三个感光器件去分别接受三个通道的强度,然后再将这三个通道的值叠加到一起就能复现出正常的颜色。这种涉及称为3CCD,这种方式大概可以用如下简图表示。
但是这种方式工艺复杂且成本较高,所以到目前位置在消费领域基本没有这种操作。
02算法原理精讲
2.1线性插值算法
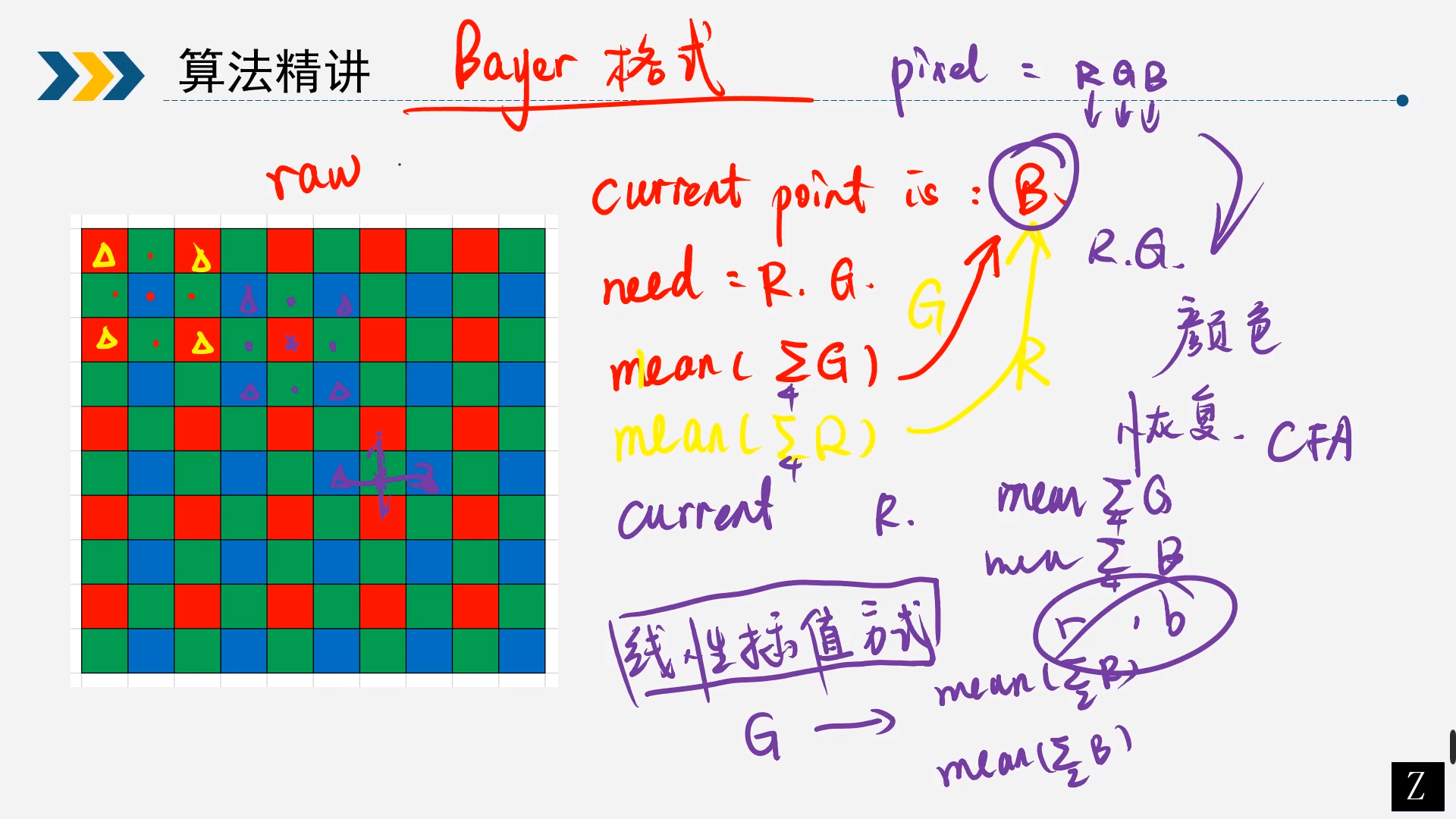
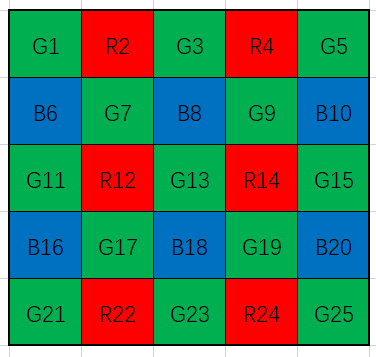
如图是Bayer格式的raw图,RGB三种颜色交替覆盖,且绿色分量是RB分量的两倍。由于这种特殊的分布方式,所以可以通过最贱的线性插值的方式通过附近的已知的颜色插值出同一通道缺失的分量。例如途中G13点为绿色,缺失了R和B,但是G13左右的R是已知的,那么就可以通过左右红色分量插值出该点缺失的红色,同理可以通过上下的蓝色分量插值出该点缺失的蓝色分量。对于R14缺失的G和B,但是周围相邻的有4个G是已知的,就可以通过这四个点插值出该点缺失的G,同理可以通过周围四个B插值出该点的B。
简化成下图所示
2.2色差法和色比法
色比法和色差法其实是基于两个假设实现插值的。
2.2.1色比法
假设再一个邻域范围内不同颜色通道的值的比值是固定的,简单来说就说相邻像素的R/G的值和B/G的值是一样的,那么设计算法时就可以利用这一点。一般情况下都会先插值出G的缺失值,然后通过与G的比值恒定插值出其他的缺失值。
如上展示的RAW图,可以通过G9,G13, G15,G19做简单的线性插值恢复G14,然后通过R14/G14 = R13/G13的假设恢复出R13。同理可以恢复出其他缺失的颜色。
举例说明,先通过线性插值法求出所有的G通道的值,然后求G7的R7和B7,最终求得B7和R7
$$
\frac{B7}{G7}=\frac{\frac{B6}{G6}+\frac{B8}{G8}}{2}\
\frac{R7}{G7}=\frac{\frac{R6}{G6}+\frac{R8}{G8}}{2}
$$
求R14对应的B14
$$
\frac{B14}{G14}=mean(\sum_4{\Delta})
=\frac{\frac{B8}{G8}+\frac{B10}{G10}+\frac{B18}{G18}+\frac{B20}{G20}}{4}
$$
2.2.2色差法
色差法和色比法类似,假设在一个邻域内不同通道的颜色插值时恒定的。只是将色比法的比值转换为差值即可。
1)通过R通道插值出G通道的值 $$ G_{m,n}=\frac{G_{m,n+1}+G_{m,n-1}}{2}+ \frac{-R_{m,n-2}+2R_{m,n}-R_{m,n+2}}{8} $$ 同理也可以通过B插值出G通道的值 $$ G_{m,n}=\frac{G_{m,n+1}+G_{m,n-1}}{2}+\frac{-B_{m,n-2}+2B_{m,n}-B_{m,n+2}}{8} $$ 2)求出R通道对应的B通道的值,举例求R43通道的B43 $$ B43-G43= \frac{(B32-G32)+(B34-G34)+(B52-G52)+(B54-G54)}{4} $$ 3)求出G通道的的B或者R通道,举例求G33通道的B33 $$ B33-G33=\frac{(B32-G32)+(B34-G34)}{2} $$ 同理可得知R33 $$ R33-G33=\frac{(R23-G23)+(R43-G43)}{2} $$
2.3基于方向加权的方法
上述简单的插值算法存在诸多缺陷,比如高频伪像和伪彩,其主要原因就是没有针对边缘做处理。所以更好的算法就对边缘做了识别,针对边缘做特殊的处理,然后同时利用色差或色比的方法融合到一起得到更好的效果
伪像
是指在图像处理的过程中,由于一些误差、干扰或技术问题造成的视觉失真或虚假的图像。
伪彩
为了增加图像的可视化效果,人们便使用了一种技术,即通过给黑白图像上色,使其在视觉上呈现出彩色的效果。这种通过对黑白图像进行着色的技术被称为伪彩。
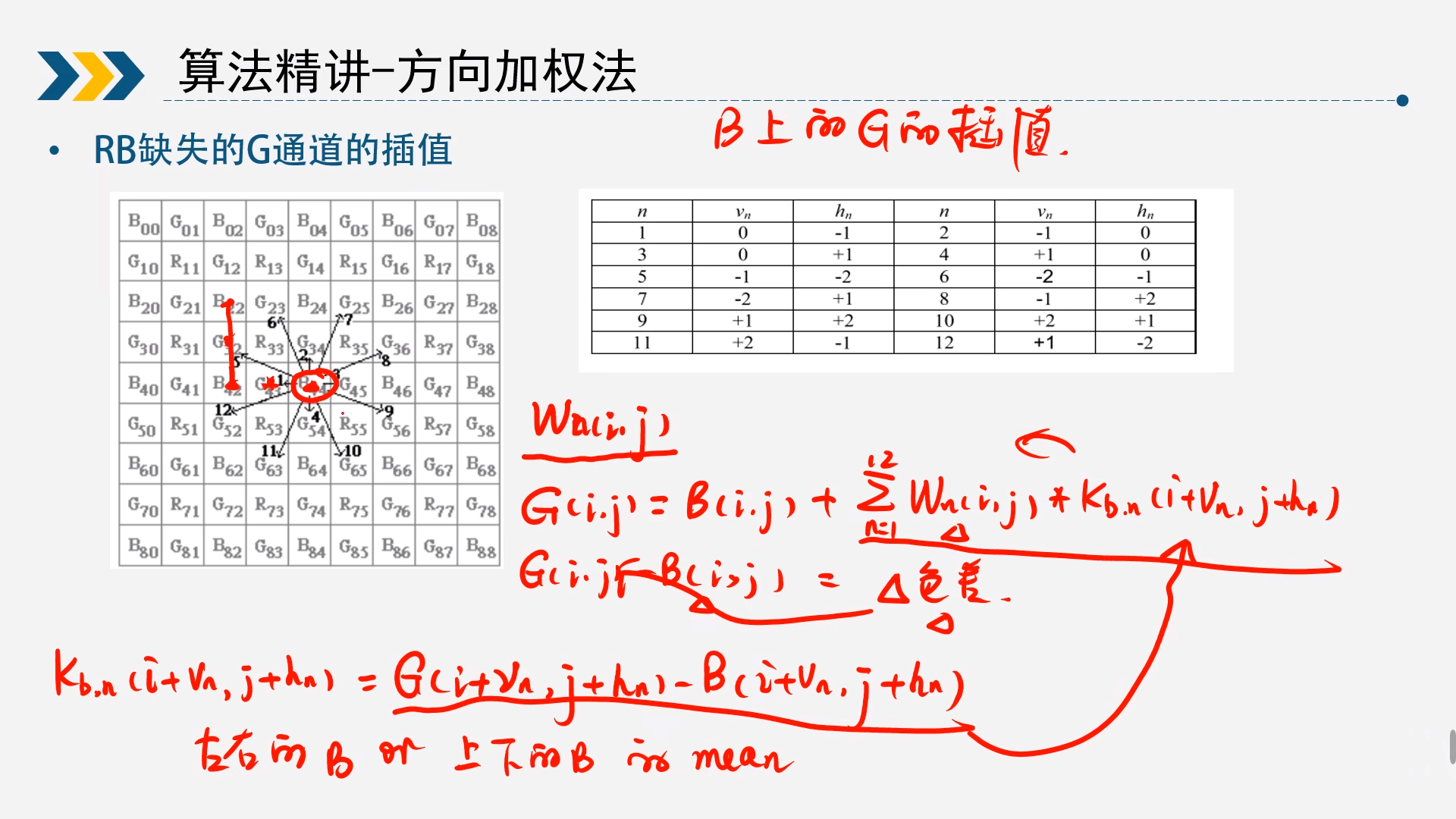
2.3.1R/B通道求G通道
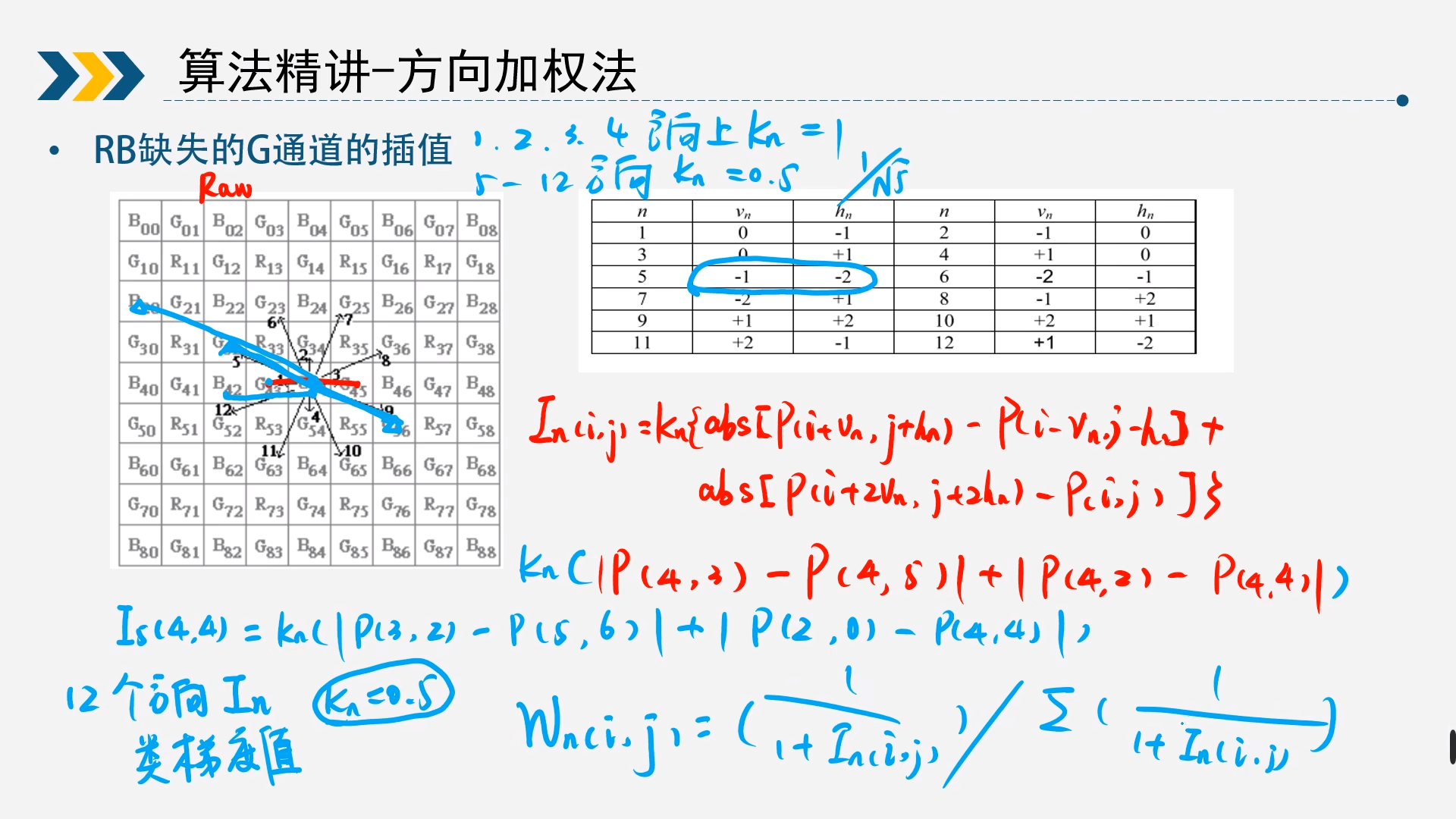
同上述算法类似,第一步求出所有像素点的G通道,这里需要9*9的bayer矩阵,以B为例,求G通道
-
计算12个梯度
梯度计算,总共有12个方向,除了上下左右之外,还有其他8个方向,需要求出所有的梯度。 $$ I_n(i,j)=k_n{abs[P(i+v_n,j+h_n)-P(i-v_n,j-h_n)]+abs[P(i+2v_n,j+2h_n)-P(i,j)]} $$ 以以B(4,4)为例 $$ I_1(4,4)=k_1{|P(4,3)-P(4,5)|+|P(4,2)-P(4,4)|}\
I_5(4,4)=k_5{|P(3,2)-P(5,6)|+|P(2,0)-P(4,4)|}
$$其中梯度中涉及到了Kn的计算,上下左右的Kn通常为1,其他边缘的值8个方向的Kn通常0.5,也可以设为其他值。
-
求出12个方向的权重
梯度越大,说明变化的范围越大。可能正好是一个边界,说明梯度大的方向插值贡献要更小一点,那么权重就会较小。 $$ W_n(i,j)=\frac{\frac{1}{1+I_n(i,j)}}{\sum_{n=1}^{12}\frac{1}{1+I_n(i,j)}} $$
-
求出色差法计算对应的G通道 $$ G(i,j)-B(i,j)=\sum_{n=1}^{12}W_n(i,j)*K_{bn}(i+v_n,j+h_n) $$ 其中公式为 $$ K_{bn}(i+v_n,j+h_n)=G(i+v_n,j+h_n)-B(i+v_n,j+h_n) $$ 因为B还没被求出来,这里的B还是按照最简单的插值来计算,举例说明B(3,2) $$ B(3,2)=(B(2,2)+B(4,2))/2 $$
以B为例,求G通道按照上面步骤可以求得,同理也可以用R通道求G通道。
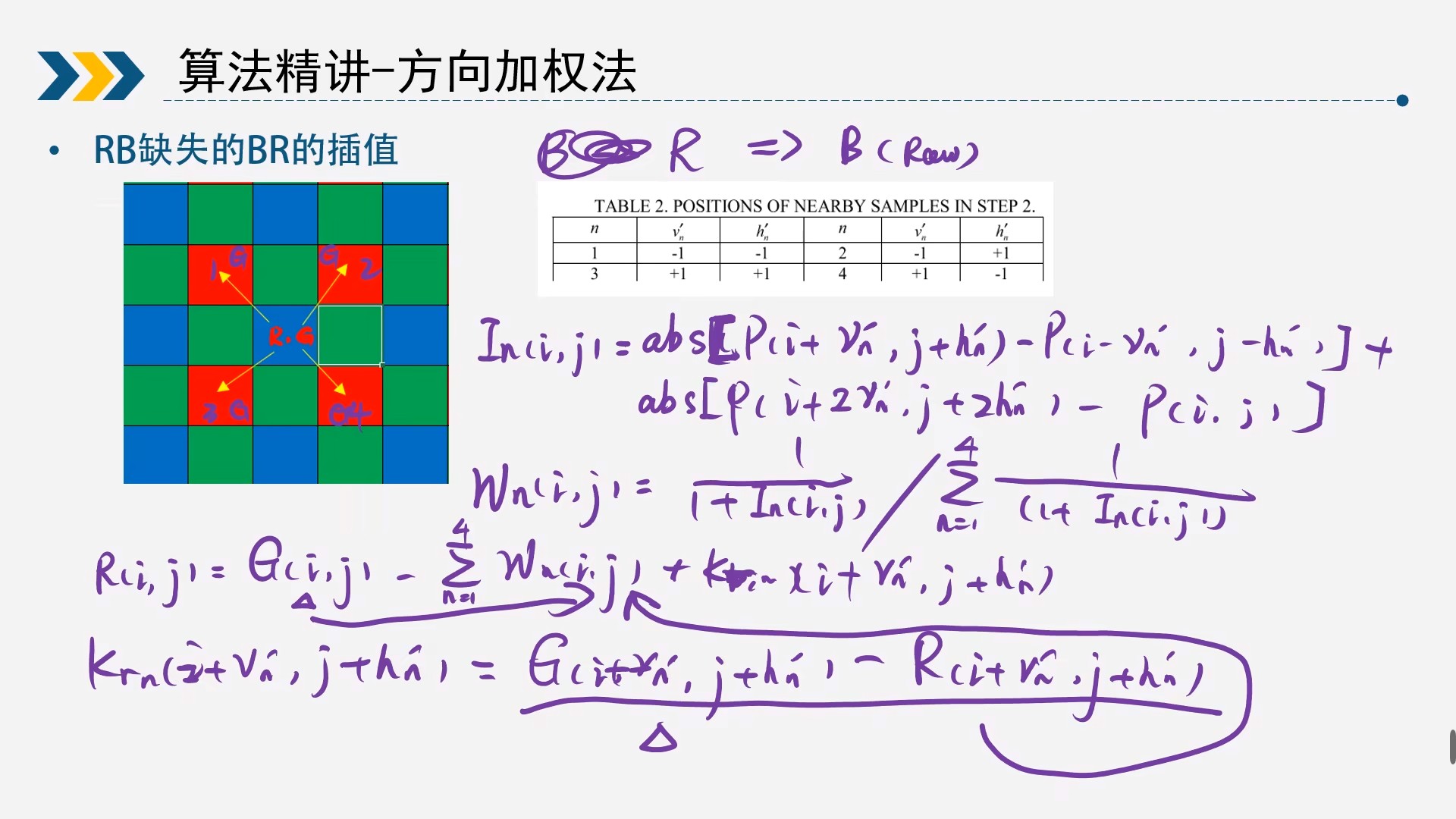
2.3.2B通道求R通道/R通道求B通道
上面步骤已经求出所有的G通道了,那么现在可以求另外R和B通道了,这里以B通道求R通道为例,这里的矩阵为5*5
公式同上面分别求梯度和权重
梯度 $$ I_n(i,j)={abs[P(i+v_n,j+h_n)-P(i-v_n,j-h_n)]+abs[P(i+2v_n,j+2h_n)-P(i,j)]} $$ 权重 $$ W_n(i,j)=\frac{\frac{1}{1+I_n(i,j)}}{\sum_{n=1}^{4}\frac{1}{1+I_n(i,j)}} $$ 那么色差法计算R通道为 $$ R(i,j)=G(i,j)-\sum_{n=1}^{4}W_n(i,j)*K_{rn}(i+v_n,j+h_n) $$ 其中公式为 $$ K_{rn}(i+v_n,j+h_n)=G(i+v_n,j+h_n)-R(i+v_n,j+h_n) $$ 以B通道求R通道就是上述方式,同理也可以R通道求B通道
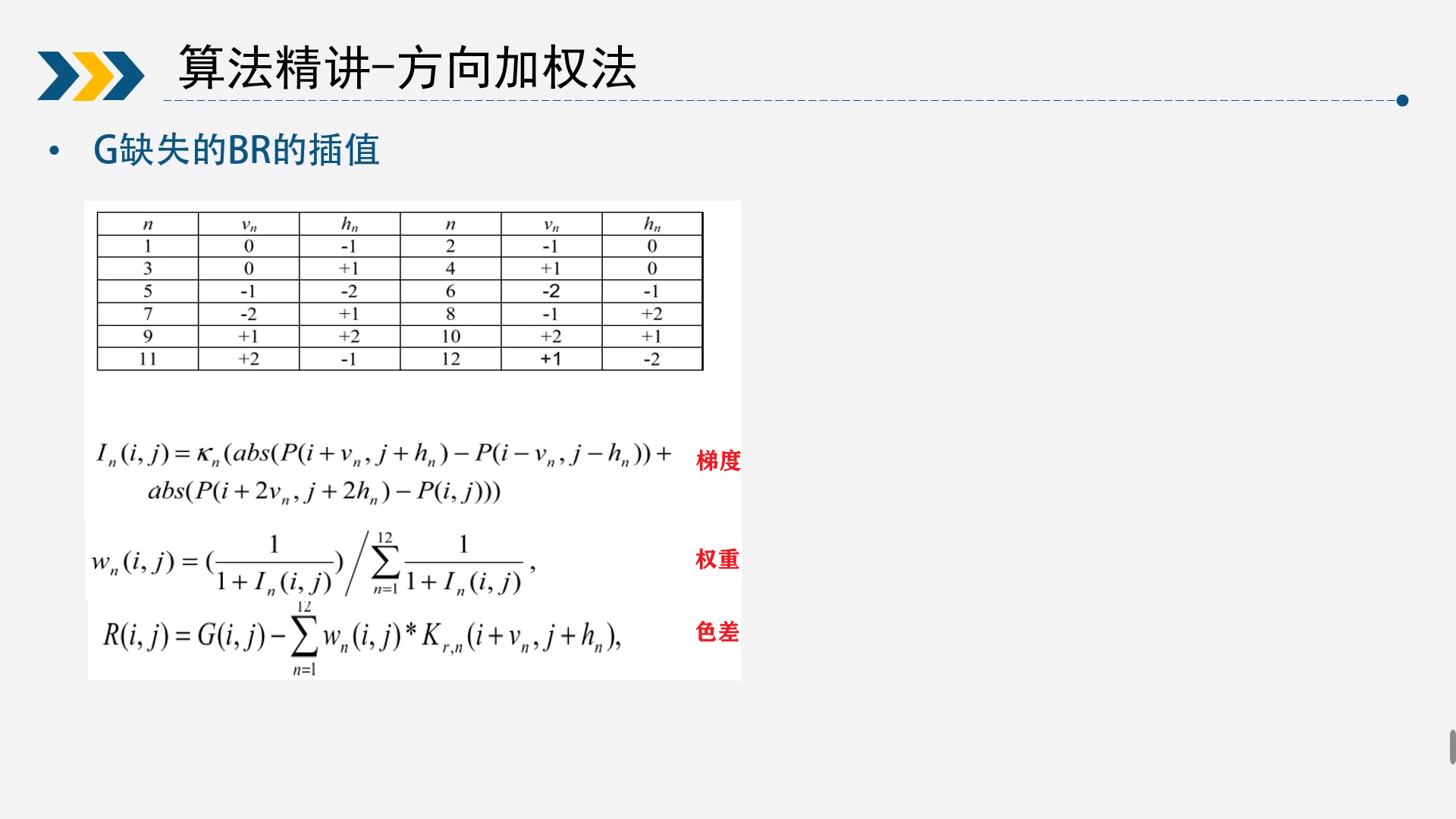
2.3.3G通道求R/B通道
上面已经对应B通道求R通道和R通道求B通道,现在还需要求G通道求R/B通道,这里以G通道求R通道为例,这里的矩阵为9*9
梯度 $$ I_n(i,j)={abs[P(i+v_n,j+h_n)-P(i-v_n,j-h_n)]+abs[P(i+2v_n,j+2h_n)-P(i,j)]} $$ 权重 $$ W_n(i,j)=\frac{\frac{1}{1+I_n(i,j)}}{\sum_{n=1}^{12}\frac{1}{1+I_n(i,j)}} $$ 色差 $$ R(i,j)=G(i,j)-\sum_{n=1}^{12}W_n(i,j)*K_{rn}(i+v_n,j+h_n) $$ 以G通道求R通道就是上述方式,同理也可以G通道求B通道
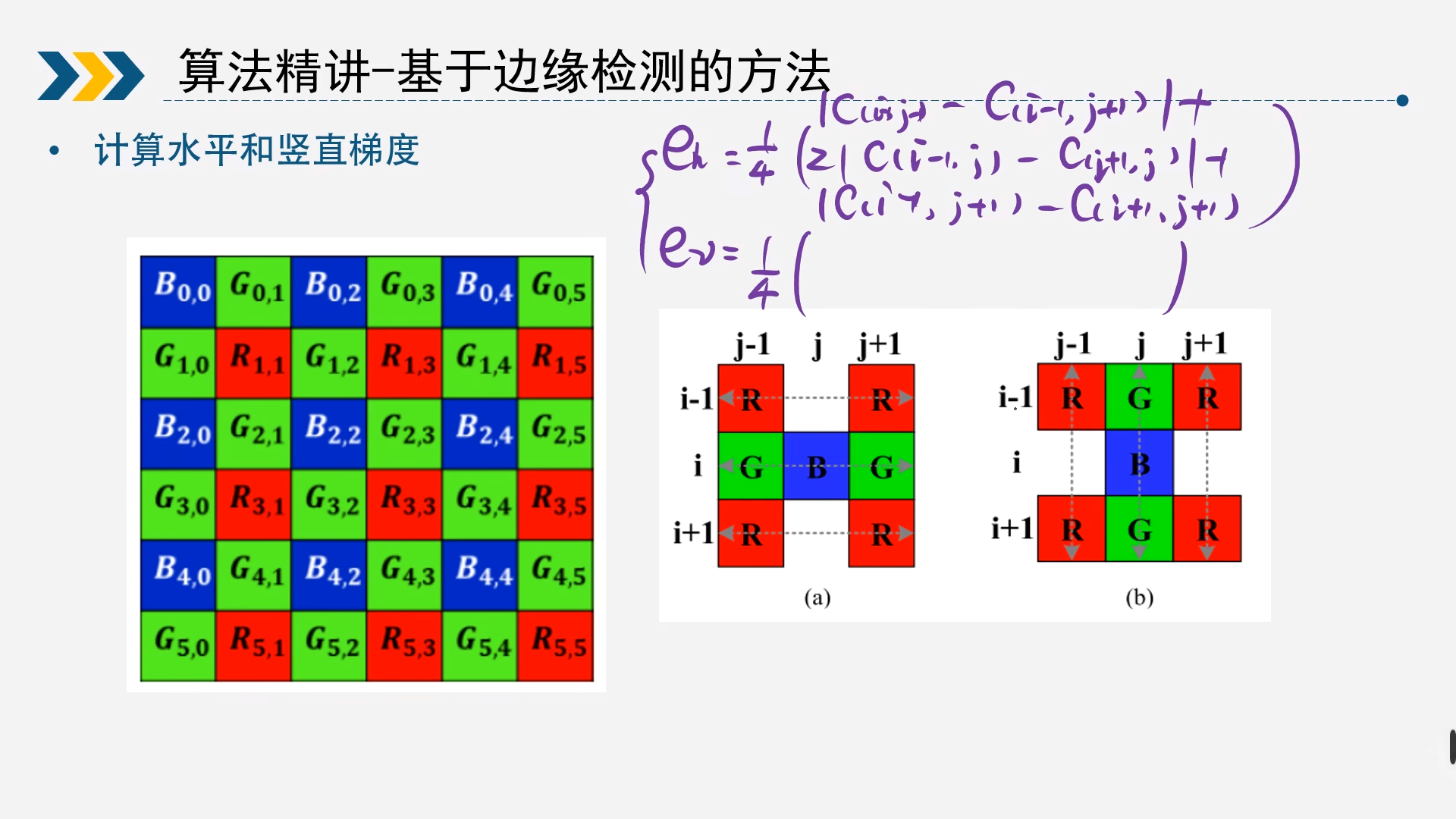
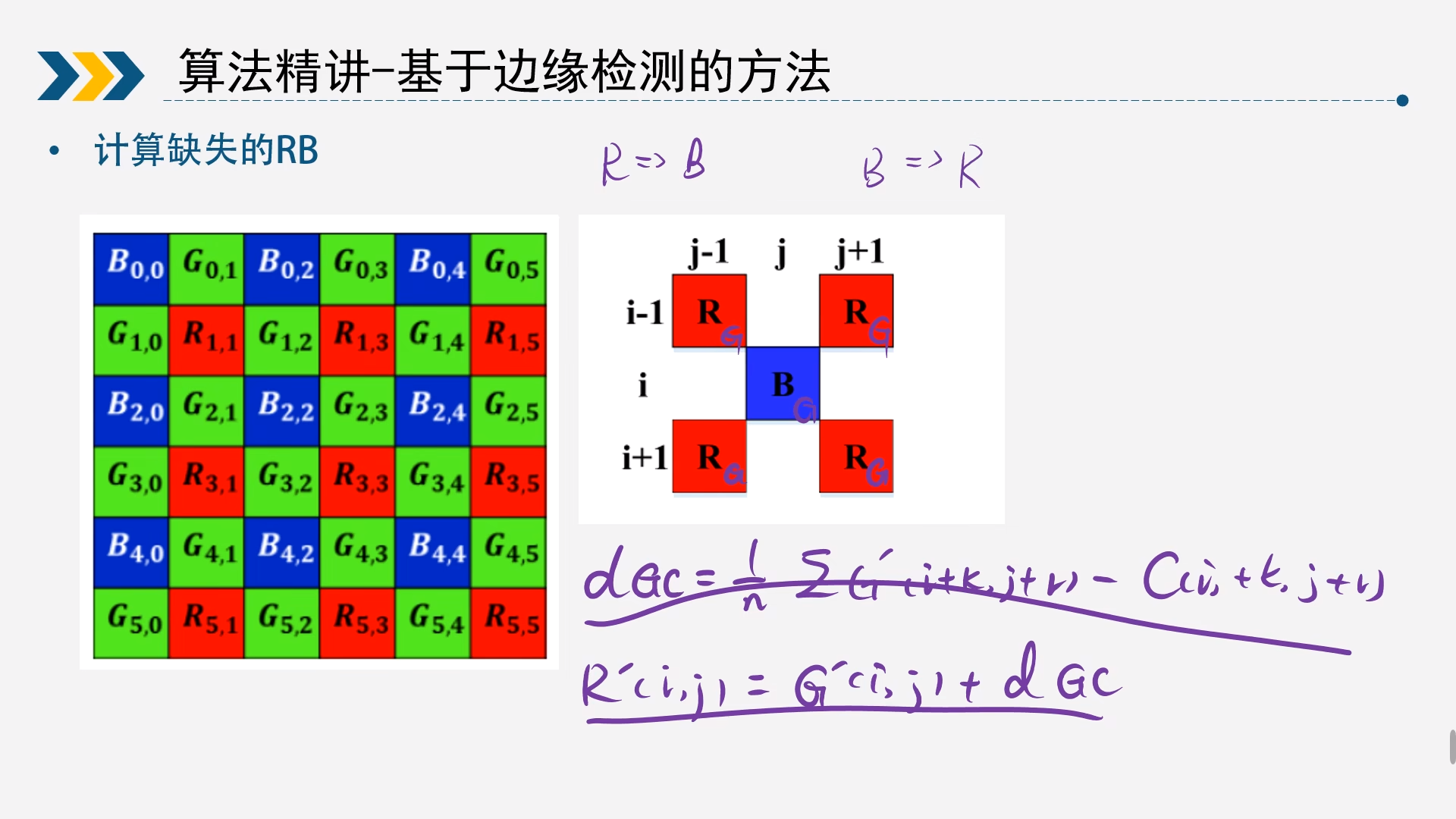
2.4基于边缘检测的方法
相比较2.3的算法,这个算法稍微简单点
2.4.1求所有的G通道
- 先求出对应梯度
- 求出对应的权重
- 先求出所有的G,然后用R求B或者B求R,最后用G求出B和R
1.梯度求解,这里以B为例求G
$$
e_h=\frac{1}{4}(|C(i-1,j-1)-C(i-1,j+1)|
+2|C(i,j-1)-C(i,j+1)|+|C(i+1,j-1)-C(i+1,j+1)|)\
e_v=\frac{1}{4}(|C(i-1,j-1)-C(i+1,j-1)|
+2|C(i-1,j)-C(i+1,j)|+|C(i-1,j+1)-C(i+1,j+1)|)
$$
2.计算权重,以R(3,3)为例,求G通道
$$
W_h=\frac{\frac{1}{e_h}}{\frac{1}{e_h}+\frac{1}{e_v}}\
W_v=\frac{\frac{1}{e_v}}{\frac{1}{e_h}+\frac{1}{e_v}}\
$$
3.求取对应的G通道
计算出R和G的平均色差,这里的C就是R通道
$$
\hat{G}_h(i,j)=\overline{G}_h(i,j)+\Delta{C_h(i,j)}\
\hat{G}_v(i,j)=\overline{G}_v(i,j)+\Delta{C_v(i,j)}
$$
其中
$$
\overline{G}_h(i,j)=\frac{1}{2}(G(i,j-1)+G(i,j+1))\
\overline{G}_v(i,j)=\frac{1}{2}(G(i-1,j)+G(i+1,j))
$$
$$
\Delta{C_h(i,j)}=\frac{1}{2}(\frac{1}{2}(C(i,j)-C(i,j-2))+\frac{1}{2}(C(i,j)-C(i,j+2)))\
\Delta{C_v(i,j)}=\frac{1}{2}(\frac{1}{2}(C(i,j)-C(i-2,j))+\frac{1}{2}(C(i,j)-C(i+2,j)))\
$$
最终 $$ G'(i,j)=W_h(i,j)\hat{G}_h(i,j)+W_v(i,j)\hat{G}_v(i,j) $$
2.4.2R通道求B通道或B通道求R通道
这里以B通道求R通道
$$ dG_c=\frac{1}{4}\sum(G'(i+k,j+r)-R(i+k,j+r))\
R'(i,j)=G'(i,j)+dG_c $$ 同理可以R通道求B通道
2.4.3G通道求R通道和B通道
跟上面B通道求R通道类似,以G(2,1)通道求R(2,1)通道为例
$$
dG_c=\frac{1}{4}\sum(G'(i+k,j+r)-R(i+k,j+r))\
R'(i,j)=G'(i,j)+dG_c
$$
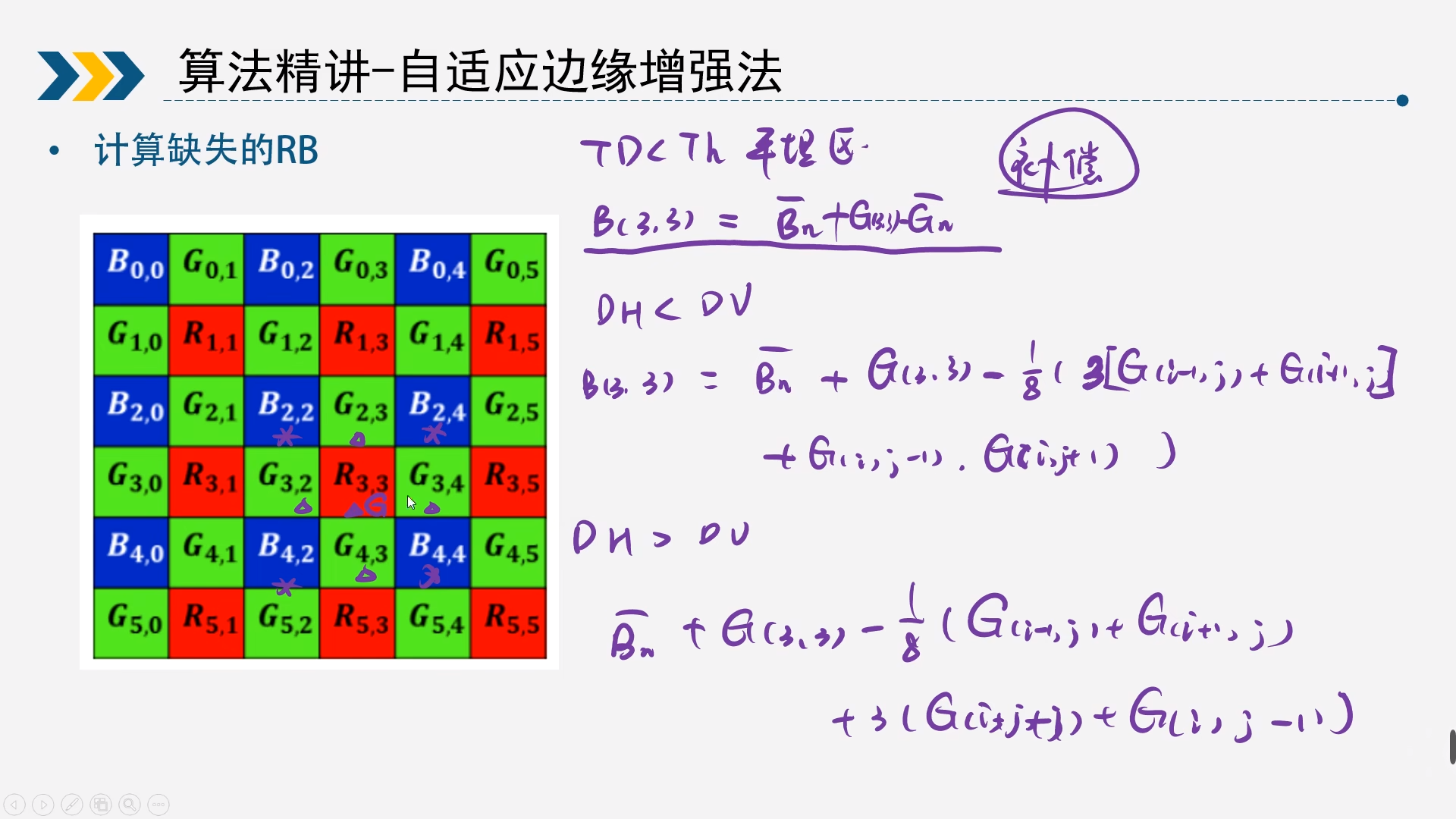
2.5自适应边缘增强法
2.5.1求所有的G通道
1)做边缘检测
2)分类讨论判断
如果是边缘检测不为边缘,那么主要还是以水平权重为主;
如果边缘检测为边缘且以竖直方向变化更大,直接求水平均值即可;
如果边缘检测为边缘且以水平方向变化更大,那么主要还是以竖直权重为主
这里以R33求G33为例说明
$$
DV(i,j)=|B(i-1,j-1)-B(i+1,j-1)|+|G(i-1,j)-G(i+1,j)|+|B(i-1,j+1)-B(i+1,j+1)|\
DH(i,j)=|B(i-1,j-1)-B(i-1,j+1)|+|G(i,j-1)-G(i,j+1)|+|B(i+1,j-1)-B(i+1,j+1)|\
$$
然后求出总的
$$
TD(i,j)=DV(i,j)+DH(i,j)
$$
分类讨论
-
TD<Th,说明未检测到边缘 $$ G(i,j)=\frac{3}{8}(G(i,j-1)+G(i,j+1))+\frac{1}{8}(G(i-1,j)+G(i+1,j))\
+R(i,j)-\frac{1}{2}(\frac{1}{2}(R(i,j)+R(i,j-2))+\frac{1}{2}(R(i,j)+R(i,j+2))) $$ -
TD>Th,说明检测到边缘
当DH<DV $$ G(i,j)=\frac{1}{2}(G(i,j-1)+G(i,j+1))\
++R(i,j)-\frac{1}{2}(\frac{1}{2}(R(i,j)+R(i,j-2))+\frac{1}{2}(R(i,j)+R(i,j+2))) $$ 当DH>DV $$ G(i,j)=\frac{3}{8}(G(i,j-1)+G(i,j+1))+\frac{1}{8}(G(i-1,j)+G(i+1,j))\
+\frac{1}{2}(R(i,j)-\frac{1}{2}(\frac{1}{2}(R(i,j)+R(i,j-2))+\frac{1}{2}(R(i,j)+R(i,j+2)))) $$
同理,B通道可以求得G通道
2.5.2R通道求出B通道或B通道求R通道
这里以R33为例,还是按照2.5.1的三种情况分类讨论
-
TD<Th,说明未检测到边缘 $$ B(3,3)=\frac{1}{4}(B(2,2)+B(2,4)+B(4,2)+B(4,4))\
+G(3,3)-\frac{1}{4}(G(2,3)+G(4,3)+G(3,2)+G(3,4)) $$ -
TD>Th,说明检测到边缘
当DH<DV $$ B(3,3)=\frac{1}{4}(B(2,2)+B(2,4)+B(4,2)+B(4,4))\
+G(3,3)-\frac{1}{8}(3G(2,3)+3G(4,3)+G(3,2)+G(3,4)) $$ 当DH>DV $$ B(3,3)=\frac{1}{4}(B(2,2)+B(2,4)+B(4,2)+B(4,4))\
+G(3,3)-\frac{1}{8}(G(2,3)+G(4,3)+3G(3,2)+3G(3,4)) $$
同理,B通道可以求得R通道
2.5.3G通道求R通道和B通道
与上述类似,不过这里以G(2,3)为例,求R(2,3)
因为G(2,3)周边的R正好为上下分布,因为竖直方向的信息量会更多
$$
R(i,j)=\frac{1}{2}(R(i-1,j)+R(i+1,j))+\frac{1}{2}G(i,j)\
-\frac{1}{8}(G(i-1,j-1)+G(i-1,j+1)+G(i+1,j-1)+G(i+1,j+1))
$$
如果是G(3,2),那么周边的R正好为左右分布
$$
R(i,j)=\frac{1}{2}(R(i,j+1)+R(i,j-1))+G(i,j)-\frac{1}{2}(G(i,j+1)+G(i,j-1))
$$
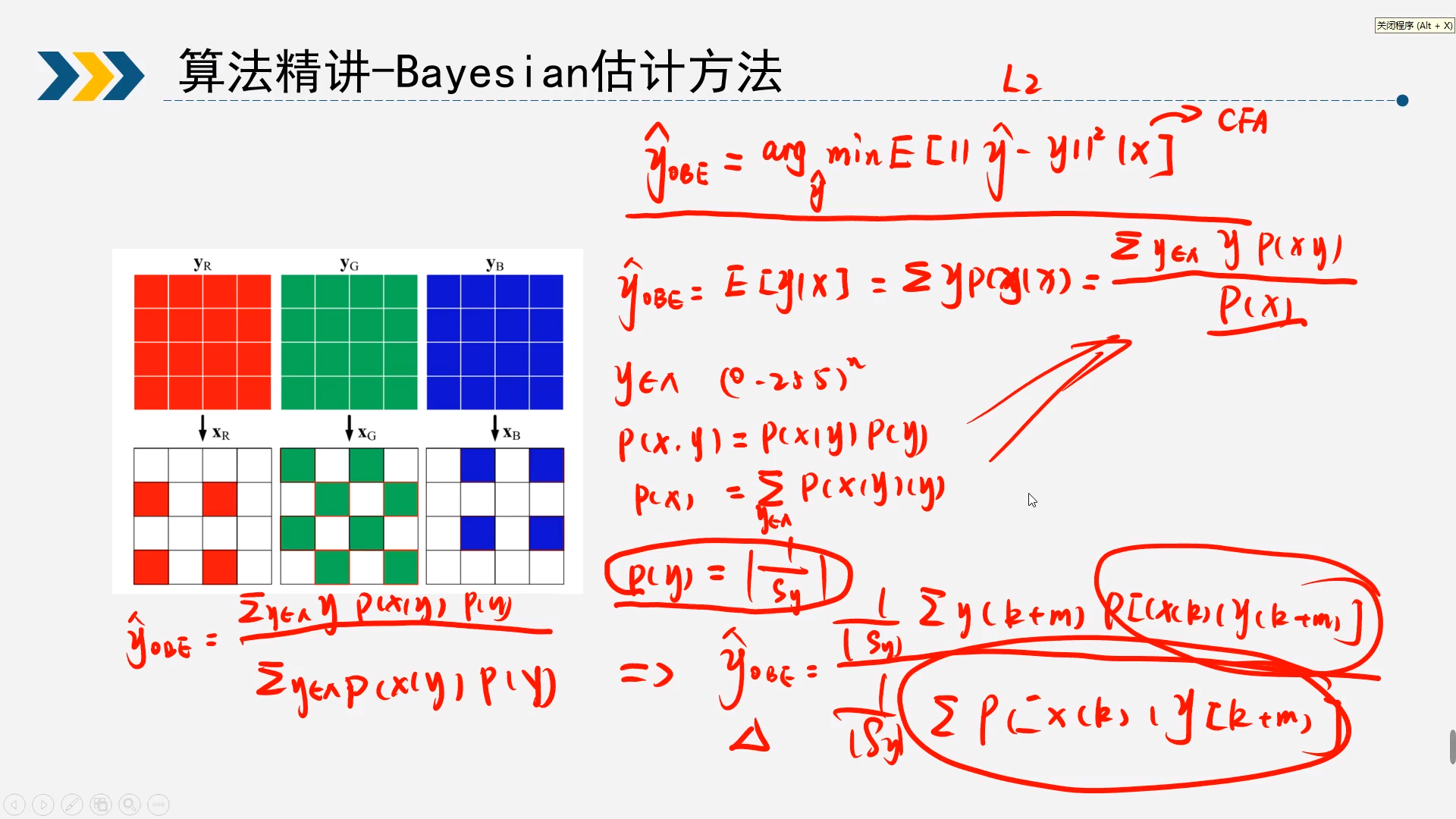
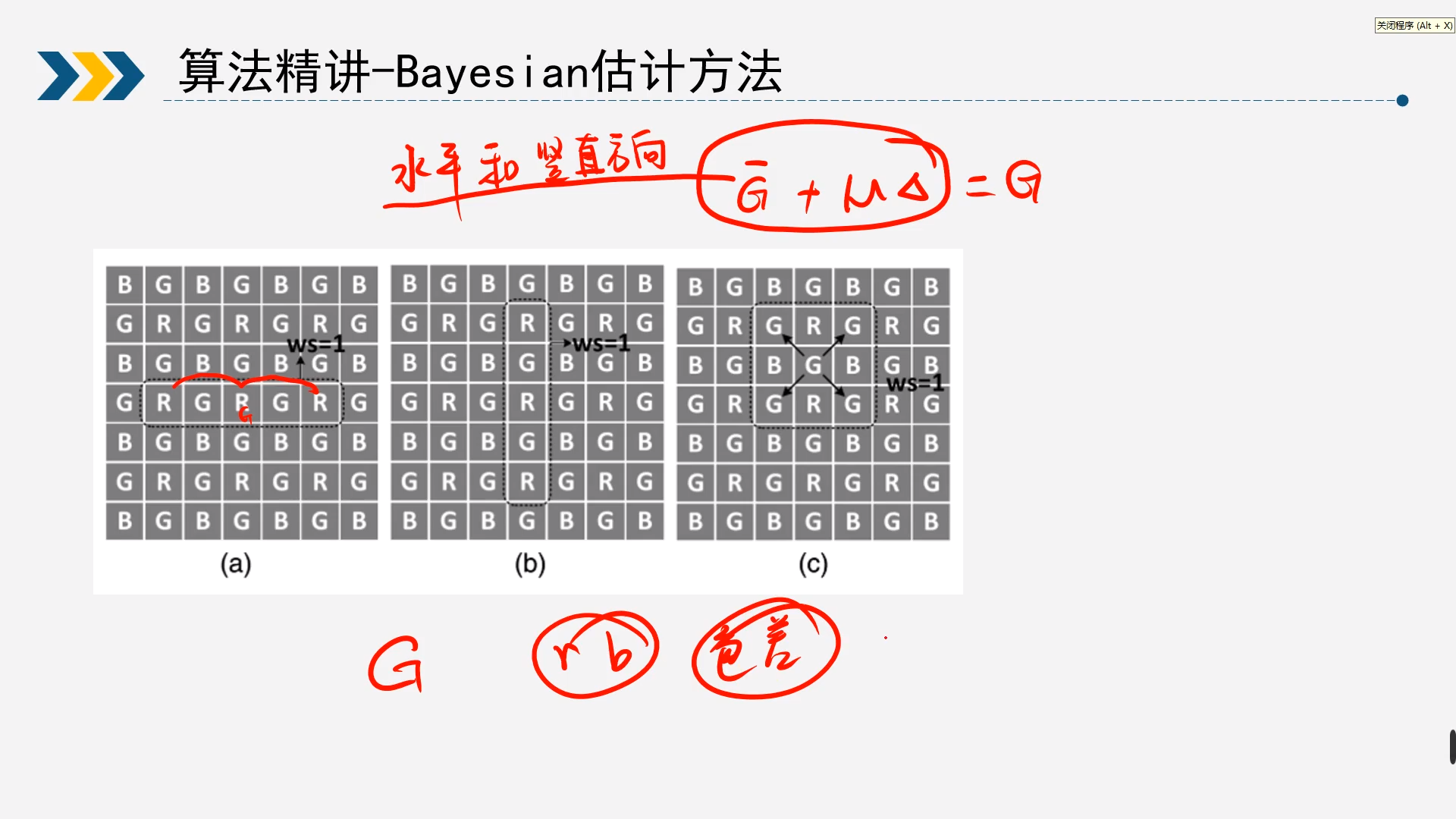
2.6Bayesian估计方法
具体不做展开,可以直接查找论文原文Bayesian method application for color demosaicking_Wang et al._2018,具体文章也可以点击这里查看
2.7深度学习-马赛克与降噪结合方法
具体论文是这篇文章Deep joint demosaicking and denoising_Gharbi et al._2016,具体文章也可以点击这里查看
2.8深度学习-残次网络模型
具体论文是这篇文章A study of two CNN demosaicking algorithms_Ehret, Facciolo_2019,具体文章也可以点击这里查看
作者的源码下载,点击这里
03算法代码实现
3.1线性插值法
1%% --------------------------------
2clc;clear;close all;
3
4%% ------------Raw Format----------------
5filePath = 'images/kodim19_8bits_RGGB.raw';
6bayerFormat = 'RGGB';
7width = 512;
8height= 768;
9bits = 8;
10%% --------------------------------------
11bayerData = readRaw(filePath, bits, width, height);
12figure();
13imshow(bayerData);
14title('raw image');
15
16%% expand image inorder to make it easy to calculate edge pixels(扩展边界)
17bayerPadding = zeros(height + 2,width+2);
18bayerPadding(2:height+1,2:width+1) = uint32(bayerData);
19bayerPadding(1,:) = bayerPadding(3,:);
20bayerPadding(height+2,:) = bayerPadding(height,:);
21bayerPadding(:,1) = bayerPadding(:,3);
22bayerPadding(:,width+2) = bayerPadding(:,width);
23
24%% main code of imterpolation
25imDst = zeros(height+2, width+2, 3);
26for ver = 2:height + 1
27 for hor = 2:width + 1
28 switch bayerFormat
29 case 'RGGB'
30 % G B -> R(把G和B插值到R上去)
31 if(0 == mod(ver, 2) && 0 == mod(hor, 2))
32 imDst(ver, hor, 1) = bayerPadding(ver, hor);
33 % G -> R
34 imDst(ver, hor, 2) = (bayerPadding(ver-1, hor) + bayerPadding(ver+1, hor) +...
35 bayerPadding(ver, hor-1) + bayerPadding(ver, hor+1))/4;
36 % B -> R
37 imDst(ver, hor, 3) = (bayerPadding(ver-1, hor-1) + bayerPadding(ver-1, hor+1) + ...
38 bayerPadding(ver+1, hor-1) + bayerPadding(ver+1, hor+1))/4;
39 % G R -> B
40 elseif (1 == mod(ver, 2) && 1 == mod(hor, 2))
41 imDst(ver, hor, 3) = bayerPadding(ver, hor);
42 % G -> B
43 imDst(ver, hor, 2) = (bayerPadding(ver-1, hor) + bayerPadding(ver+1, hor) +...
44 bayerPadding(ver, hor-1) + bayerPadding(ver, hor+1))/4;
45 % R -> B
46 imDst(ver, hor, 1) = (bayerPadding(ver-1, hor-1) + bayerPadding(ver-1, hor+1) + ...
47 bayerPadding(ver+1, hor-1) + bayerPadding(ver+1, hor+1))/4;
48 elseif(0 == mod(ver, 2) && 1 == mod(hor, 2))
49 imDst(ver, hor, 2) = bayerPadding(ver, hor);
50 % R -> Gr
51 imDst(ver, hor, 1) = (bayerPadding(ver, hor-1) + bayerPadding(ver, hor+1))/2;
52 % B -> Gr
53 imDst(ver, hor, 3) = (bayerPadding(ver-1, hor) + bayerPadding(ver+1, hor))/2;
54 elseif(1 == mod(ver, 2) && 0 == mod(hor, 2))
55 imDst(ver, hor, 2) = bayerPadding(ver, hor);
56 % B -> Gb
57 imDst(ver, hor, 3) = (bayerPadding(ver, hor-1) + bayerPadding(ver, hor+1))/2;
58 % R -> Gb
59 imDst(ver, hor, 1) = (bayerPadding(ver-1, hor) + bayerPadding(ver+1, hor))/2;
60 end
61 case 'GRBG'
62 continue;
63 case 'GBGR'
64 continue;
65 case 'BGGR'
66 continue;
67 end
68 end
69end
70imDst = uint8(imDst(2:height+1,2:width+1,:));
71figure,imshow(imDst);title('demosaic image');
72
73orgImage = imread('images/kodim19.png');
74figure, imshow(orgImage);title('org image');
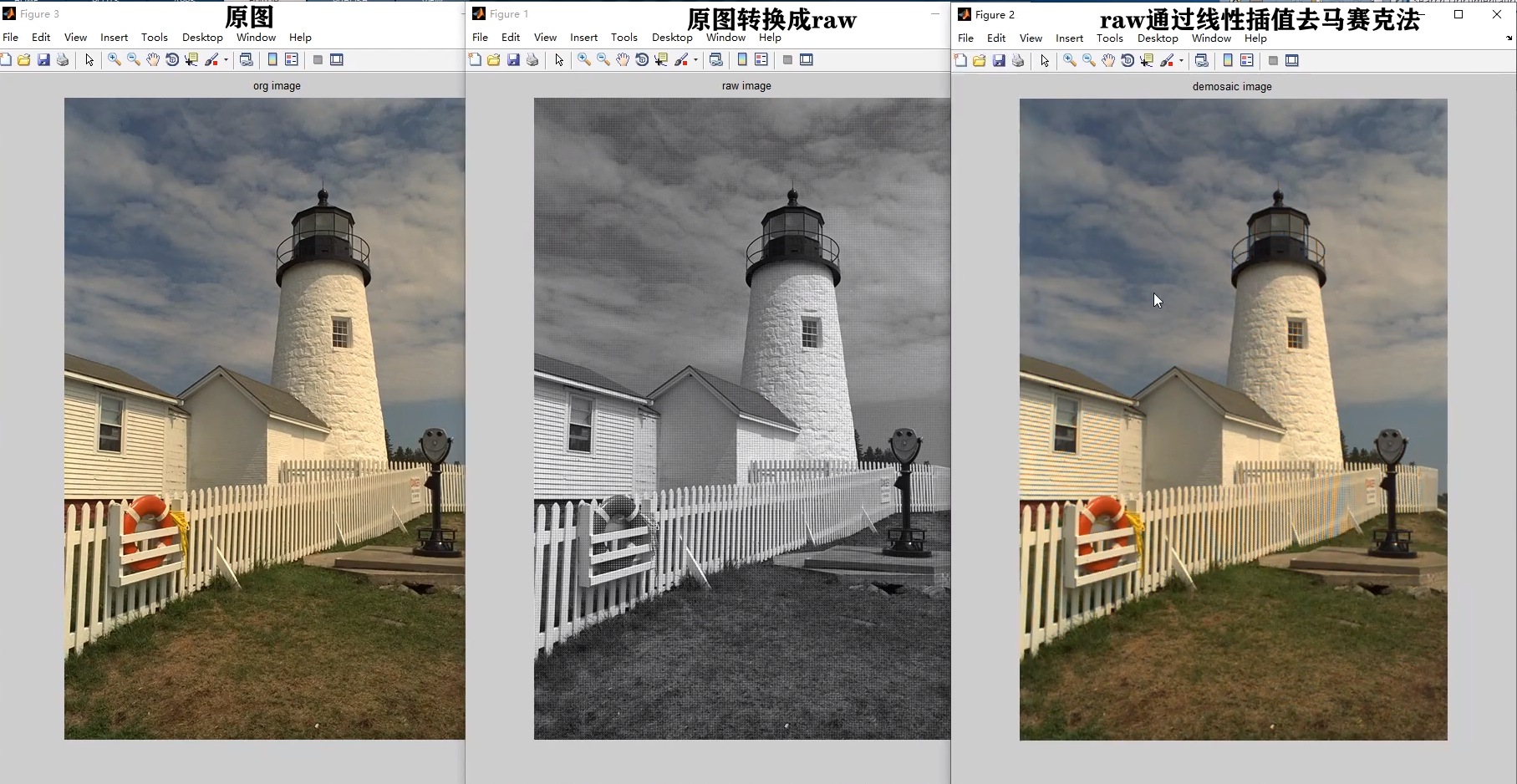
左侧是实验原图,右侧是通过上述的简单的线性插值出来的效果,从图中可以看出简单的线性插值出来得到效果一般。存在画面整体清晰度变差,高频存在伪彩,边缘又伪像。
3.2基于方向加权的算法
1clc;clear;close all;
2
3%% ------------Raw Format----------------
4filePath = 'images/kodim19_8bits_RGGB.raw';
5bayerFormat = 'RGGB';
6width = 512;
7height= 768;
8bits = 8;
9
10%% ------------Global Value--------------
11RC = 1;
12GC = 2;
13BC = 3;
14
15%% --------------------------------------
16orgImg = imread('images/kodim19.png');
17figure();imshow(orgImg);title('org image');
18
19bayerData = readRaw(filePath, bits, width, height);
20figure();
21imshow(bayerData);
22title('raw image');
23
24%% expand image inorder to make it easy to calculate edge pixels
25addpath('../publicFunction');
26bayerPadding = expandRaw(bayerData, 4);
27
28imDst = zeros(height+8, width+8, 3);
29
30%% Interpolate the missing green value of blue/red samples
31for ver = 5: height + 4
32 for hor = 5: width +4
33 % R channal
34 if(1 == mod(ver, 2) && 1 == mod(hor, 2))
35 imDst(ver, hor, 1) = bayerPadding(ver, hor);
36 neighborhoodData = bayerPadding(ver-4: ver+4, hor-4: hor+4);
37 Wn = DW_Wn(neighborhoodData, 12);
38 Kn = DW_Kn(neighborhoodData, 12);
39 imDst(ver, hor, 2) = bayerPadding(ver, hor) + sum(Wn .* Kn);
40 % B channal
41 elseif (0 == mod(ver, 2) && 0 == mod(hor, 2))
42 imDst(ver, hor, 3) = bayerPadding(ver, hor);
43 neighborhoodData = bayerPadding(ver-4: ver+4, hor-4: hor+4);
44 Wn = DW_Wn(neighborhoodData, 12);
45 Kn = DW_Kn(neighborhoodData, 12);
46 imDst(ver, hor, 2) = bayerPadding(ver, hor) + sum(Wn .* Kn);
47 % Gr
48 elseif (1 == mod(ver, 2) && 0 == mod(hor, 2))
49 imDst(ver, hor, 2) = bayerPadding(ver, hor);
50 % Gb
51 elseif (0 == mod(ver, 2) && 1 == mod(hor, 2))
52 imDst(ver, hor, 2) = bayerPadding(ver, hor);
53 end
54 end
55end
56
57% expand the imDst
58imDst(:, 1: 4, :) = imDst(:, 5: 8, :);
59imDst(:, width+5: width+8, :) = imDst(:, width+1: width+4, :);
60imDst(1:4, : , :) = imDst(5: 8, :, :);
61imDst(height+5: height+8, : , :) = imDst(height+1: height+4, :, :);
62
63%% Interpolate the missing red/blue values of blue/red samples.
64for ver = 5: height + 4
65 for hor = 5: width +4
66 % R channal
67 if(1 == mod(ver, 2) && 1 == mod(hor, 2))
68 neighborRaw = bayerPadding(ver-4: ver+4, hor-4: hor+4);
69 Wn = DW_Wn(neighborRaw, 4);
70 neighborhoodData = imDst(ver-4: ver+4, hor-4: hor+4, :);
71 Kn = DW_Kn(neighborhoodData, 4, BC);
72 imDst(ver, hor, 3) = imDst(ver, hor, 2) - sum(Wn .* Kn);
73 % B channal
74 elseif (0 == mod(ver, 2) && 0 == mod(hor, 2))
75 neighborRaw = bayerPadding(ver-4: ver+4, hor-4: hor+4);
76 Wn = DW_Wn(neighborRaw, 4);
77 neighborhoodData = imDst(ver-4: ver+4, hor-4: hor+4, :);
78 Kn = DW_Kn(neighborhoodData, 4, RC);
79 imDst(ver, hor, 1) = imDst(ver, hor, 2) - sum(Wn .* Kn);
80 else
81 continue
82 end
83 end
84end
85% expand the imDst
86imDst(:, 1: 4, :) = imDst(:, 5: 8, :);
87imDst(:, width+5: width+8, :) = imDst(:, width+1: width+4, :);
88imDst(1:4, : , :) = imDst(5: 8, :, :);
89imDst(height+5: height+8, : , :) = imDst(height+1: height+4, :, :);
90
91%% Interpolate missing red/blue values of green samples.
92for ver = 5: height + 4
93 for hor = 5: width +4
94 neighborhoodData = imDst(ver-4: ver+4, hor-4: hor+4, :);
95 % R channal
96 if(1 == mod(ver, 2) && 1 == mod(hor, 2))
97 continue
98 % B channal
99 elseif (0 == mod(ver, 2) && 0 == mod(hor, 2))
100 continue
101 % G
102 else
103 Wrn = DW_Wn(neighborhoodData, 12, GC, RC);
104 Wbn = DW_Wn(neighborhoodData, 12, GC, BC);
105 Krn = DW_Kn(neighborhoodData, 12, RC);
106 Kbn = DW_Kn(neighborhoodData, 12, BC);
107 imDst(ver, hor, 1) = imDst(ver, hor, 2) - sum(Wrn .* Krn);
108 imDst(ver, hor, 3) = imDst(ver, hor, 2) - sum(Wbn .* Kbn);
109 end
110 end
111end
112% expand the imDst
113imDst(:, 1: 4, :) = imDst(:, 5: 8, :);
114imDst(:, width+5: width+8, :) = imDst(:, width+1: width+4, :);
115imDst(1:4, : , :) = imDst(5: 8, :, :);
116imDst(height+5: height+8, : , :) = imDst(height+1: height+4, :, :);
117figure();imshow(uint8(imDst));title('now');
118
119%% Adjust the estimated green values of red/blue samples
120for ver = 5: height + 4
121 for hor = 5: width +4
122 neighborhoodData = imDst(ver-4: ver+4, hor-4: hor+4, :);
123 % R channal
124 if(1 == mod(ver, 2) && 1 == mod(hor, 2))
125 Wrn = DW_Wn(neighborhoodData, 12, RC, GC);
126 Krn = DW_Kn(neighborhoodData, 12, RC);
127 imDst(ver, hor, 2) = imDst(ver, hor, 1) + sum(Wrn .* Krn);
128 % B channal
129 elseif (0 == mod(ver, 2) && 0 == mod(hor, 2))
130 Wbn = DW_Wn(neighborhoodData, 12, BC, GC);
131 Kbn = DW_Kn(neighborhoodData, 12, BC);
132 imDst(ver, hor, 2) = imDst(ver, hor, 3) + sum(Wbn .* Kbn);
133 % G
134 else
135 continue
136 end
137 end
138end
139demosaicImg = imDst(5: height + 4, 5: width +4, :);
140figure();imshow(uint8(demosaicImg));title('demosaicking image');
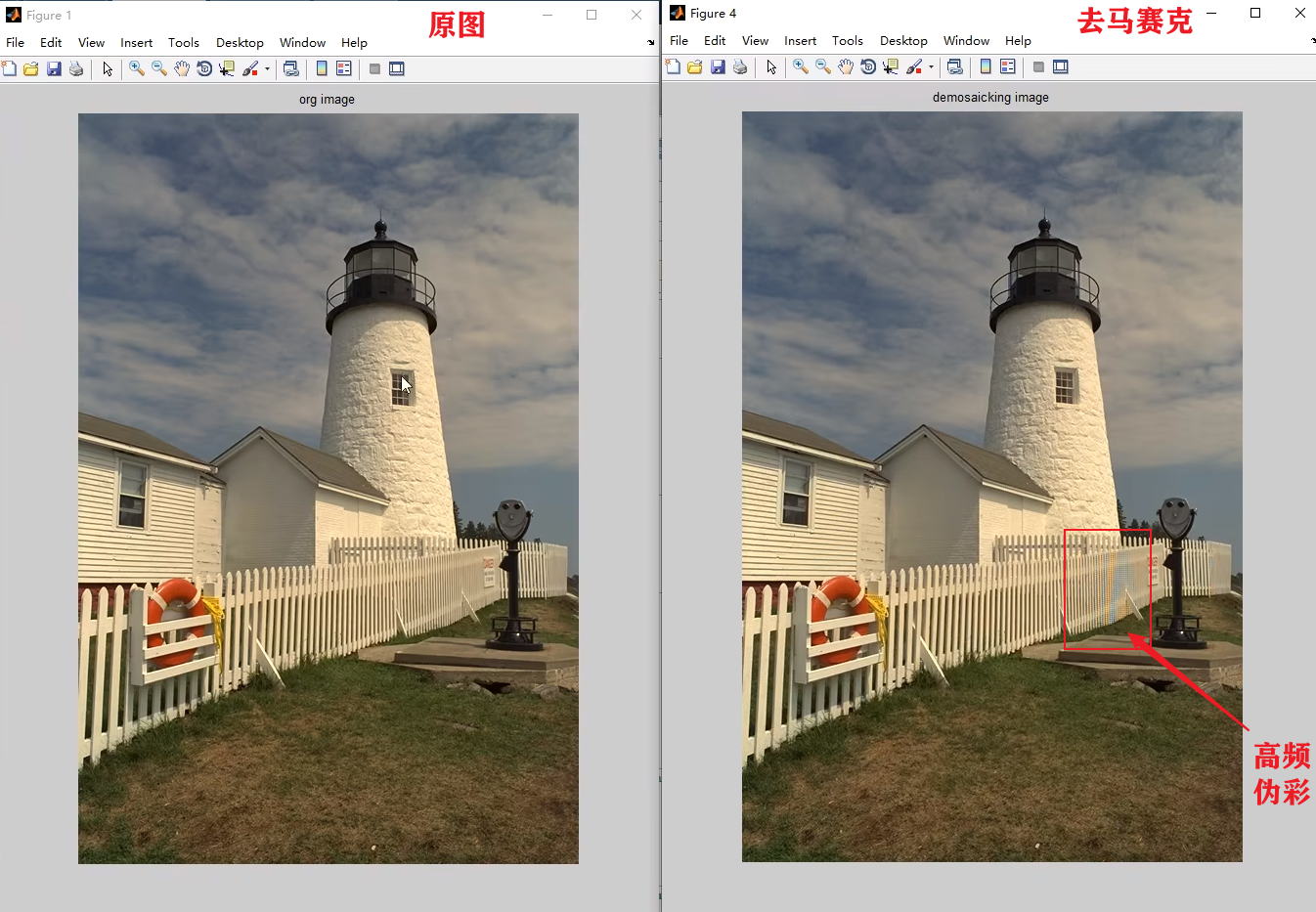
虽然还是会存在高频伪彩,但是相比较3.1的线性插值,这个效果更接近原图的效果
3.3深度学习法
通过机器学习或者深度学习的方法来处理ISP的流程也是一个新的探索,所以在这个环节也引进了相关的算法
1import torchvision
2from torch import nn
3import torch
4import cv2 as cv
5import matplotlib.pyplot as plt
6from DeepJointDemosaickingAndDenoising import DJDDNetwork
7import argparse
8import numpy as np
9
10
11# todo rgb2raw
12def rgb2raw(org_img):
13 """
14 G B
15 R G
16 """
17 mos = np.copy(org_img)
18 mask = np.zeros(org_img.shape)
19 # red
20 mask[0::2, 1::2, 0] = 1
21
22 # green
23 mask[0::2, 0::2, 1] = 1
24 mask[1::2, 1::2, 1] = 1
25
26 # blue
27 mask[1::2, 0::2, 2] = 1
28
29 masic_image = mos * mask
30
31 raw = masic_image.astype(np.uint8)
32 return raw
33
34
35def main(args):
36 # todo org-> cfa
37
38 model = DJDDNetwork()
39 # model.load_state_dict(torch.load("model_GPU_2000.pth"))
40 model = torch.load("model_cpu_100.pth")
41 model.eval()
42 # raw = cv.imread("../../images/00025_raw.png")
43 org_img = cv.imread(args.input)
44 org_rgb_img = cv.cvtColor(org_img, cv.COLOR_BGR2RGB)
45 plt.figure()
46 plt.imshow(org_rgb_img)
47 plt.title("org")
48
49 raw = rgb2raw(org_img)
50 cv.imwrite(args.output_mosaicked, raw, [cv.IMWRITE_PNG_COMPRESSION, 0])
51 plt.figure()
52 plt.imshow(raw)
53 plt.title("raw")
54
55 # ndarray to tensor
56 transform = torchvision.transforms.ToTensor()
57 tensor_raw = transform(raw)
58 # Turn 3 dimensions into 4 dimensions that model need
59 tensor_raw = torch.unsqueeze(tensor_raw, dim=0)
60 # 4 dimensions tensor to 3 dimensions np.array
61 output = (model(tensor_raw)[0].detach().numpy().transpose(1, 2, 0) * 255).astype('uint8')
62 img = cv.cvtColor(output, cv.COLOR_BGR2RGB)
63 cv.imwrite(args.output, output, [cv.IMWRITE_PNG_COMPRESSION, 0]) # , [int(cv.IMWRITE_JPEG_QUALITY), 100]
64 print("output shape: {}".format(img.shape))
65 plt.figure()
66 plt.imshow(img)
67 plt.title("output")
68 plt.show()
69
70
71if __name__ == '__main__':
72 parser = argparse.ArgumentParser()
73 parser.add_argument("--input", type=str, default="kodim19.png", help="path to input image.")
74 parser.add_argument("--output", type=str, default="output.png", help="path to output image.")
75 parser.add_argument("--output_mosaicked", type=str, default="cfa.png", help="path to ouput cfa image")
76 args = parser.parse_args()
77 main(args)
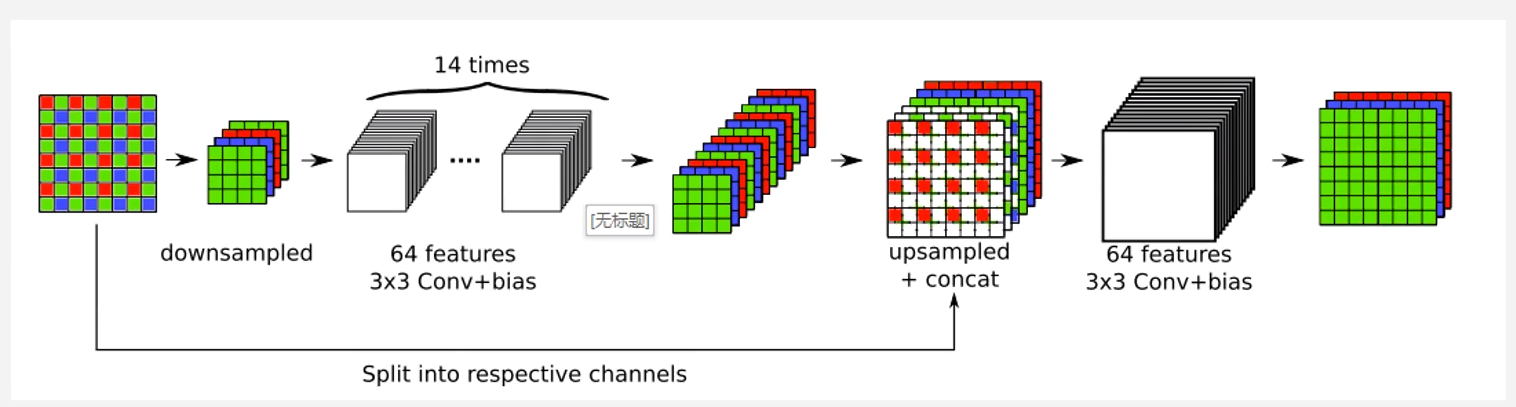
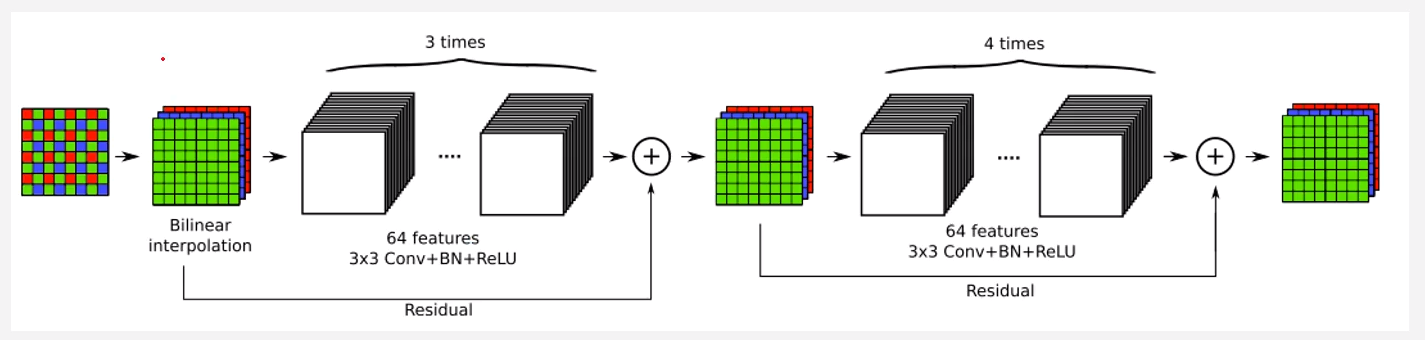
这里需要提一点的就是,该算法默认的raw输入为3通道,这个图可以通过一通道的raw生成,就是只保留该点原本的颜色值,其他两个通道为0即可。大体模型就是输入的RAW先通过降采样生成4通道的长宽均缩小一半的数据,这里降采样有两种方式,一种是直接将图像拆分为R,B,Gr,和Gb四个通道,然后再进网络,另一种方式就是如图代码中的方式,通过一个2X2,步长为2的卷积核进行一个卷积运算输出一个4通道。在经过降采样后再经过14次3X3的卷积并用ReLu作为激活函数,同时整个过程维持64通道。然后在15层通过3X3卷积输出一个12通道的数据,紧接着通过一个上采样卷积生成一个3通道的数据,然后将这个3通道的数据和原始的raw数据做一个叠加生成一个6通道的数据,紧接着再经过一个3X3卷积生成64通道数据,最后再通过一个3X3的卷积生成最终的图像。基于这个模型通过大量的数据来学习最终生成一个效果OK的模型。由于手头算力有限,所以我这边训练的模型效果一般,但是作者通过230万张图片经过2-3周的训练,可以得到一个很OK的模型。关于这个模型在我的仓库中提供了pytorch和paddle两个版本,具体可以点击这里