isp算法学习-BNR(Bayer Noise Reduce)
1400 Words|Read in about 7 Min|本文总阅读量次
本文是isp算法学习的第十篇章,主要是讲述BNR原理和算法。
1BNR意义
RAW图上的噪声模型通常用高斯-泊松模型进行描述,但是在PIPELINE中每经过一个处理模块,噪声都会发相应的变化,在经过一些列的线性和非线性变化后噪声模型会变得更加复杂,很难通过模型去降低噪声了。
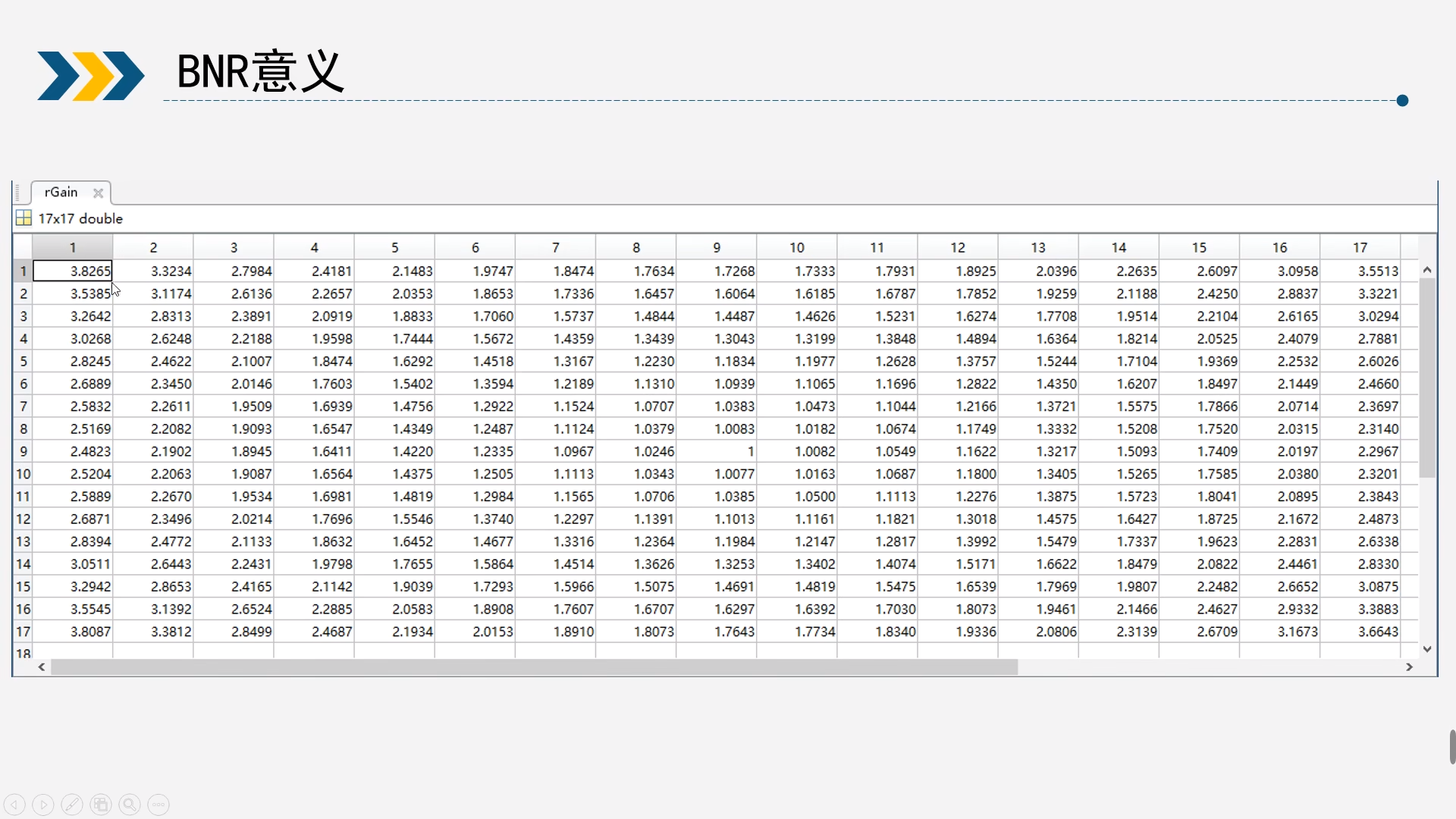
如图是前面介绍LSC时标定得到的补偿Gain值,可以发现四周的gain值(顶点3倍gain)会比中间的大(中心1倍gain)很多,这样就会导致原本均匀分布的噪声在不同的gain值作用下变得不均匀,切这种不均匀和镜头相关,噪声模型就会变得复杂。
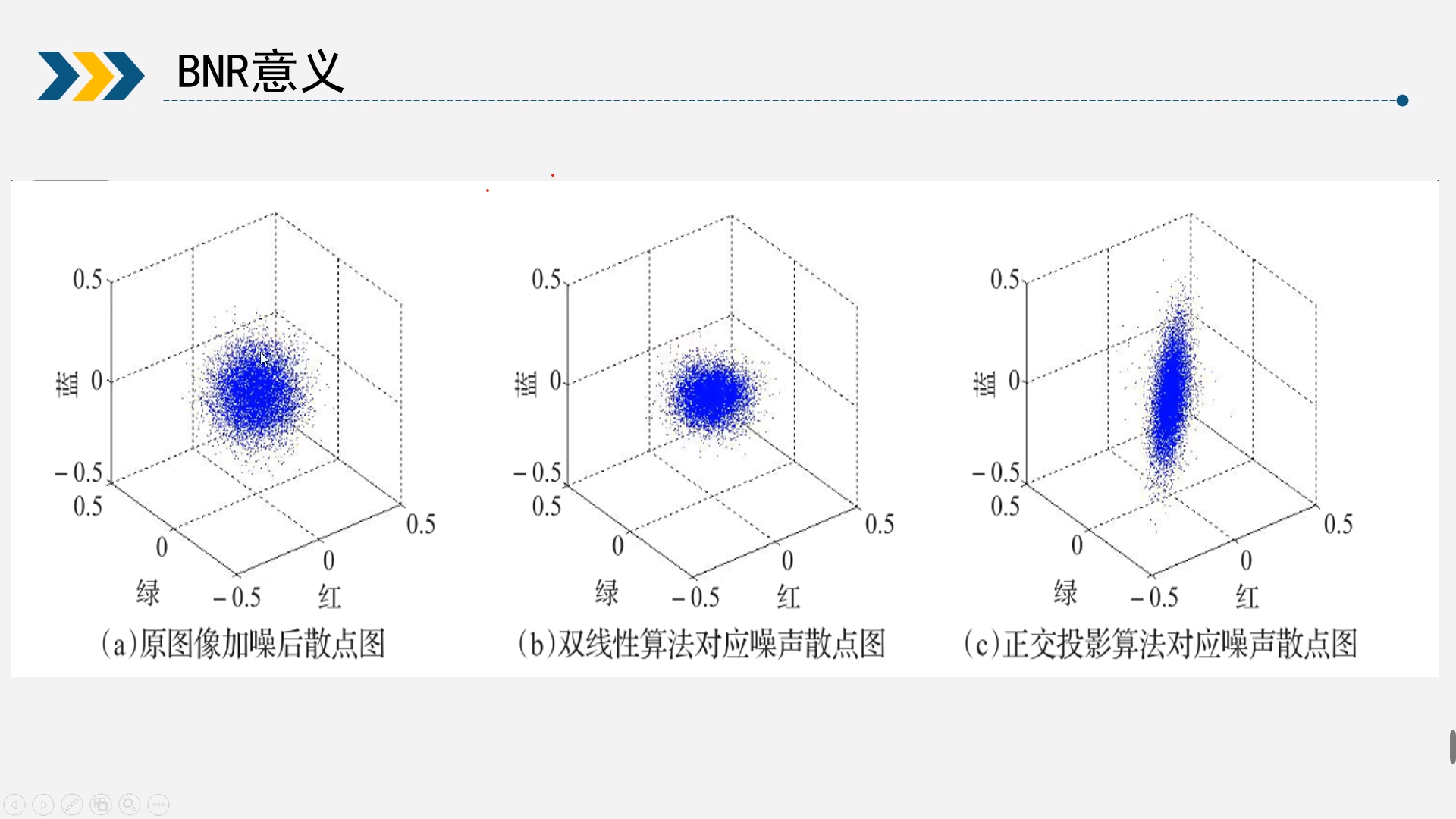
如图时去马赛克算法对噪声模型的影响,可以看出不同的马赛克算法对噪声模型的改变程度和方式都会有所差异,导致经过去马赛克后噪声模型无法确定。
除此之外pipeline中还会经过Gamma,CCM,AWB等一系列线性和非线性的变换,会使得噪声模型更加复杂,后面再想去除噪声会变得更加困难,所以一种很理想的方式就是直接在RAW上就对噪声进行抑制,让噪声在一个合理的范围内。
2校正方法
本文主要介绍三种RAW域的降噪算法,其中两种基于PCA(主成分分析Principal Component Analysis)的方式降噪,另一中是基于HVS的方式降噪,其中还涉及到的PCA和小波变换去噪。
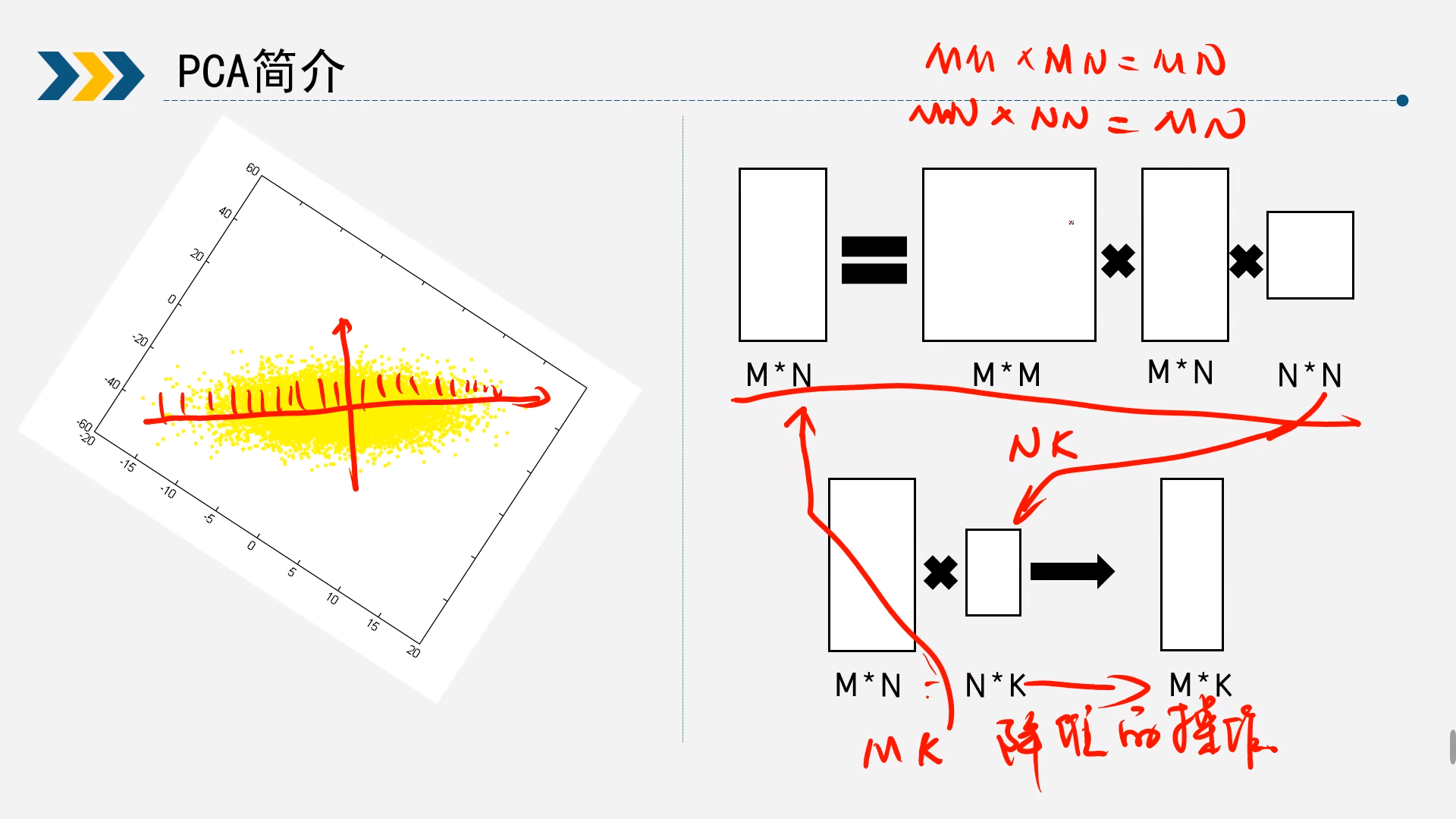
2.1PCA简介
一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维,具体可以点击这里。
- S(信号)集中分布于主成分维度
- N(噪声)平均分布于每个维度
假设有10个维度
1S:
240% 30% 20% 5% 2% 1% 0.8% 0.6% 0.4% 0.2%
3N:
410% 10% 10% 10% 10% 10% 10% 10% 10% 10%
通过PCA方法,取信号的前5个维度
1s'=40%+30%+20%+5%+2%=97%
2N'=10%+10%+10%+10%+10%=50%
3原先的信噪比SNR=S/N=1
4现在的信噪比SNR'=S'/N'=97%/50%>1(达到了降噪的目的)
如下图所示
2.1.1Based Spatially Adaptive Denoising of CFA Images for Single
PCA-Based Spatially Adaptive Denoising of CFA Images for Single-Sensor Digital Cameras(基于空间自适应的单传感器数字相机CFA图像去噪)
PCA降噪的主要依据就是噪声是均匀分布的,而图像的有用信息主要分布在主成的特征上,所以经过PCA降维后图像的主要信息得到了保留,而噪声随着减少的维度损失掉了,那么再经过反PCA变换后SNR就可以得到提升。
该算法的主要思路就是首先在整副图中选择一个区域,即图中最大的黑框(原文称之为training block)。PCA需要有特征,那么需要选择特征框(variable block),即图中小框。如图我们将特征框的尺寸定义为6*6(这个可以根据情况自行选择效果好的),假设小框的排列为Gr,R,B,Gb,那么我们就可以得到一个
$$
[Gr1,R1,Gr2,R2…B1,Gb1,B2,Gb2…]
$$
的一个列向量,那么在training block中有多少个小框,那么就有多少个这样的列向量,假设有255个小框,那么就可以组成一个36*255的矩阵,其中36代表有36个特征,255代表有255个数据。
为了进一步提高算法的效果,在这255个数据中找出相似区域做PCA,因为不相似区域的贡献度太高在后续的去马赛克算法中会使得图像容易出现伪彩。这里找相似的方式,作者使用的方式是通过求每个列向量与中心向量(图中绿色框)的曼哈顿距离来排序,然后选择距离相近的N个数据作为最终的PCA数据。经过处理后数据就变为36*N维。然后再对这个二维数据进行主成分分析,找出前m维个特征进行降维(这个m是对36个特征进行处理)。然后再对降维后的数据进行反PCA变换就可以起到降噪的功效。
除了这些简单的操作,原文中还有一些提升效果的操作,比如主成分的变换矩阵是通过模型求的没有噪声特性的图像的变换矩阵,这样在对图像进行PCA变换的时候就可以降低噪声对图像主成分的干扰,然后文中PCA之前会通过小波得到噪声模型的方差,用来分析噪声
2.1.2PSEUDO FOUR-CHANNEL IMAGE DENOISING FOR NOISY CFA RAWDATA
这种方法只是用来作为一个思路,因为需要的内存较大,还没验证在实际PIPELINE上的效果。
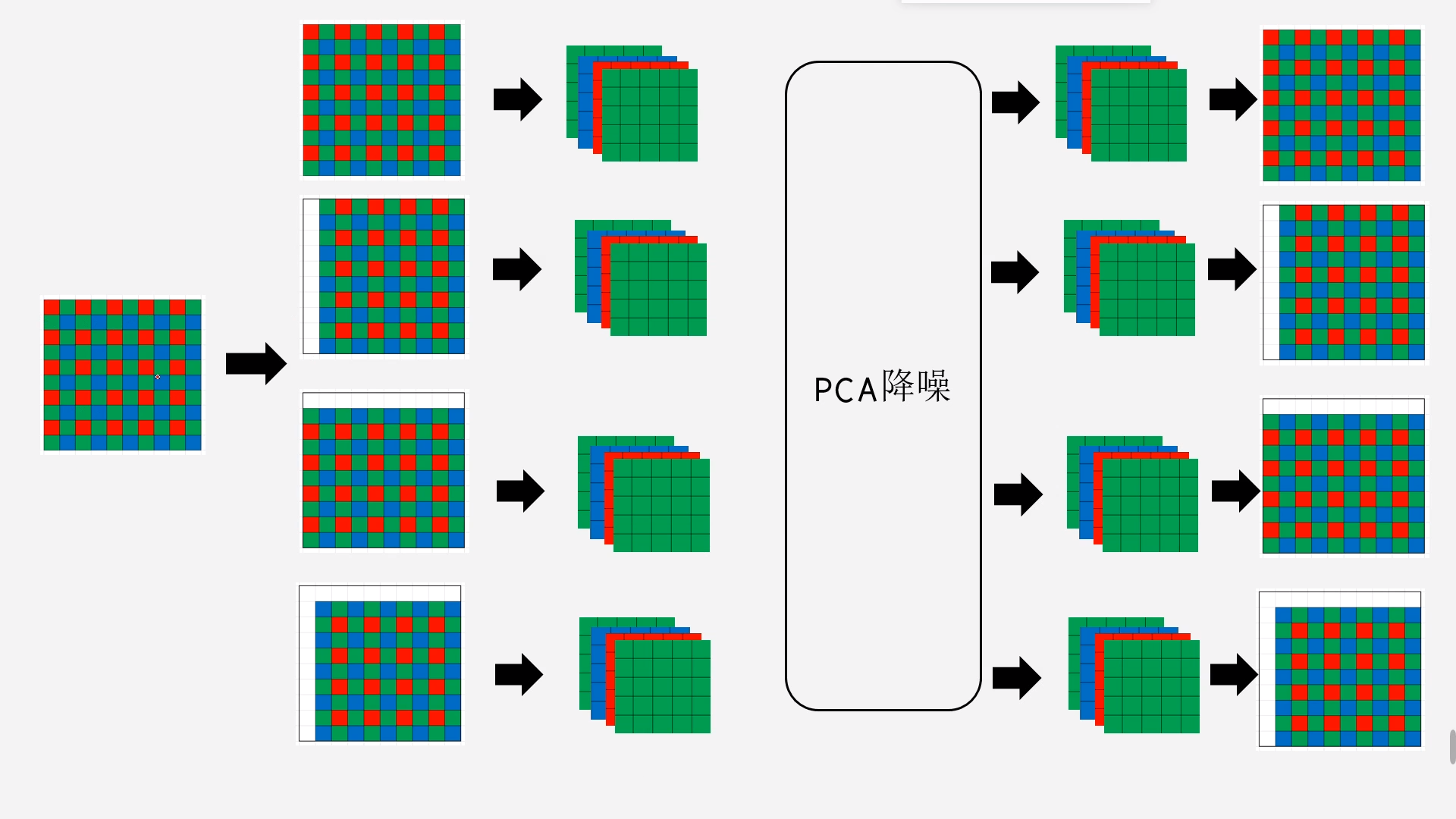
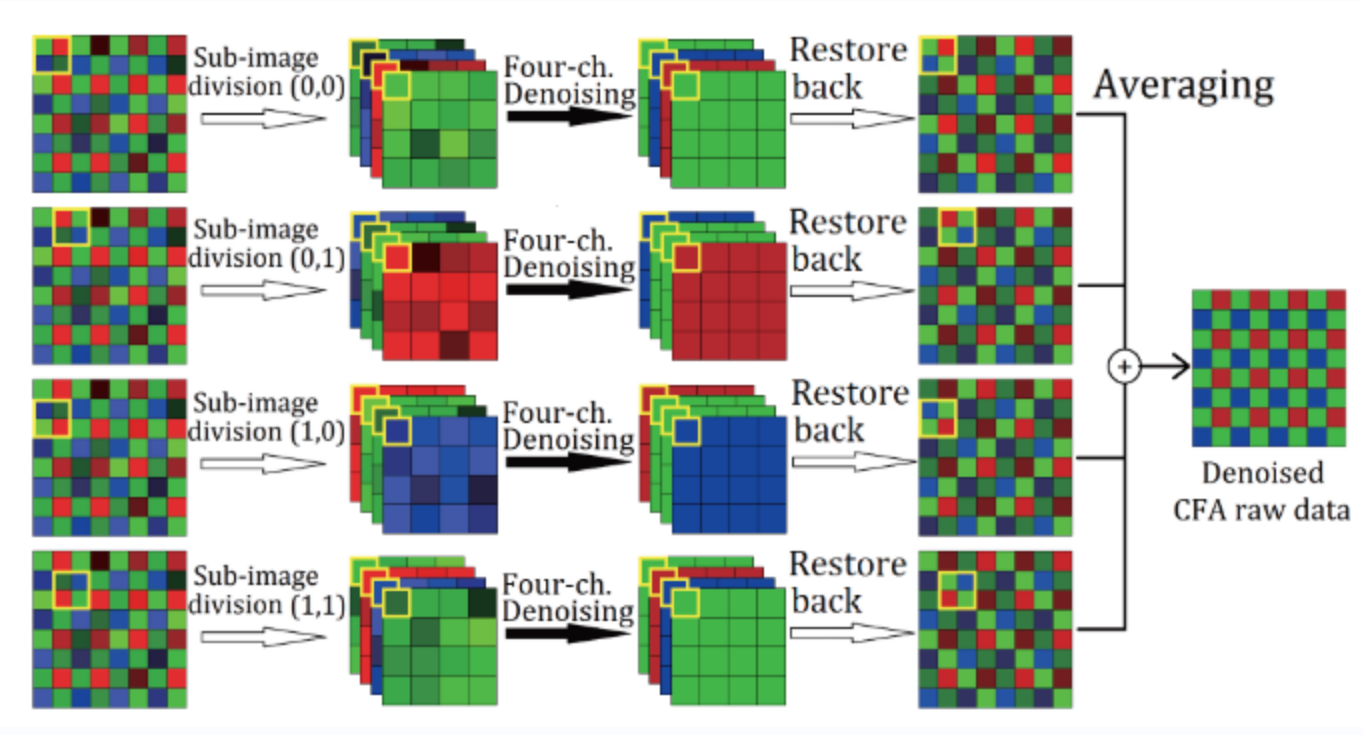
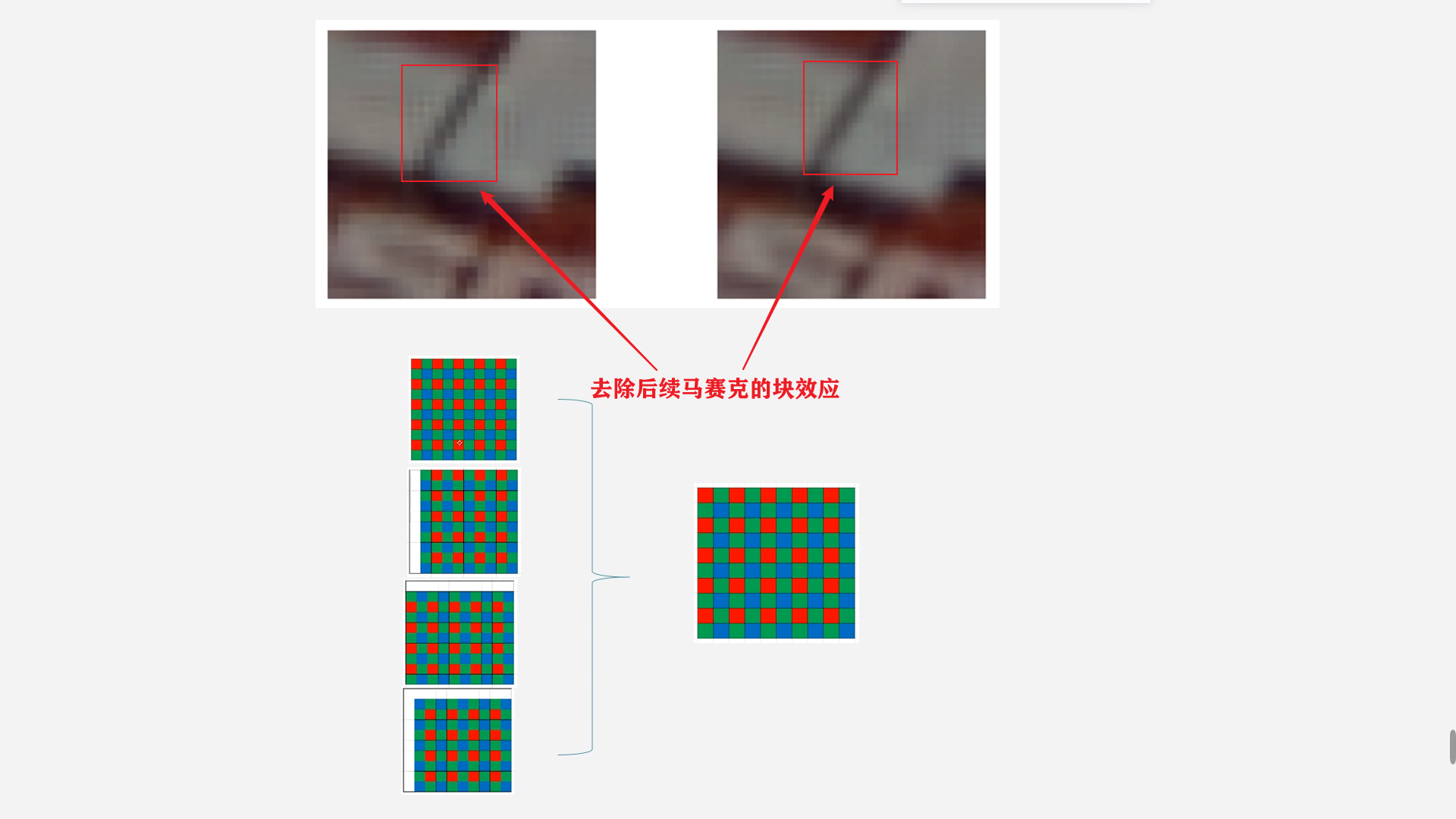
主要思路就是将一个选择不同的起始点得四种不同的数据,然后对这四种数据进行PCA降噪,然后再次展开成四张RAW图,然后对四张RAW进行平均得到最终的raw图。
至于四张RAW图的作用,是用来消除块效应的
2.2其他算法
2.2.1Noise Reduction for CFA Image Sensors Exploiting HVS Behaviour
方法主要是结合HVS进行bayer域的降噪,具体HVS可以点击这里。
2.2.1.1噪声模型
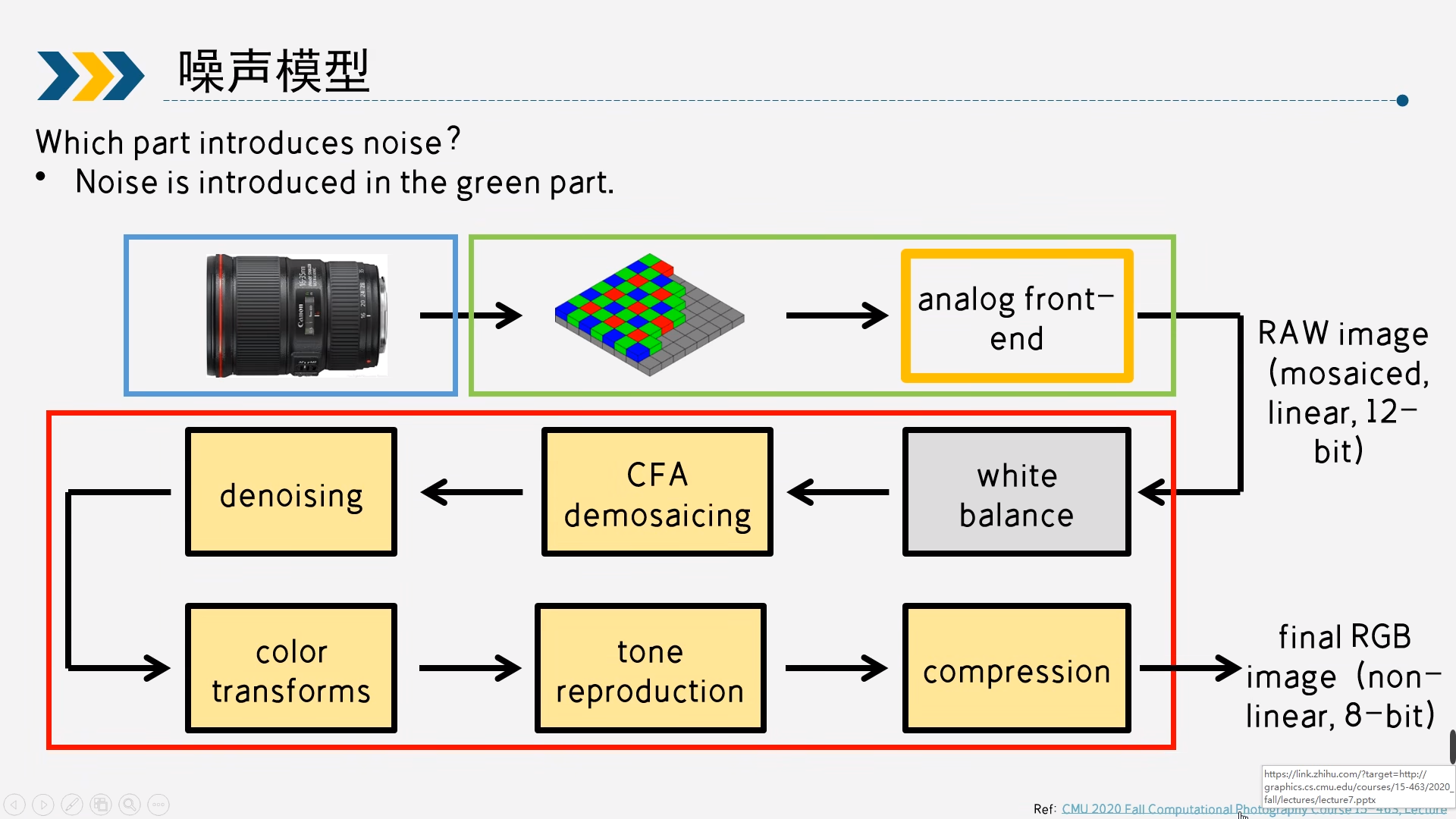
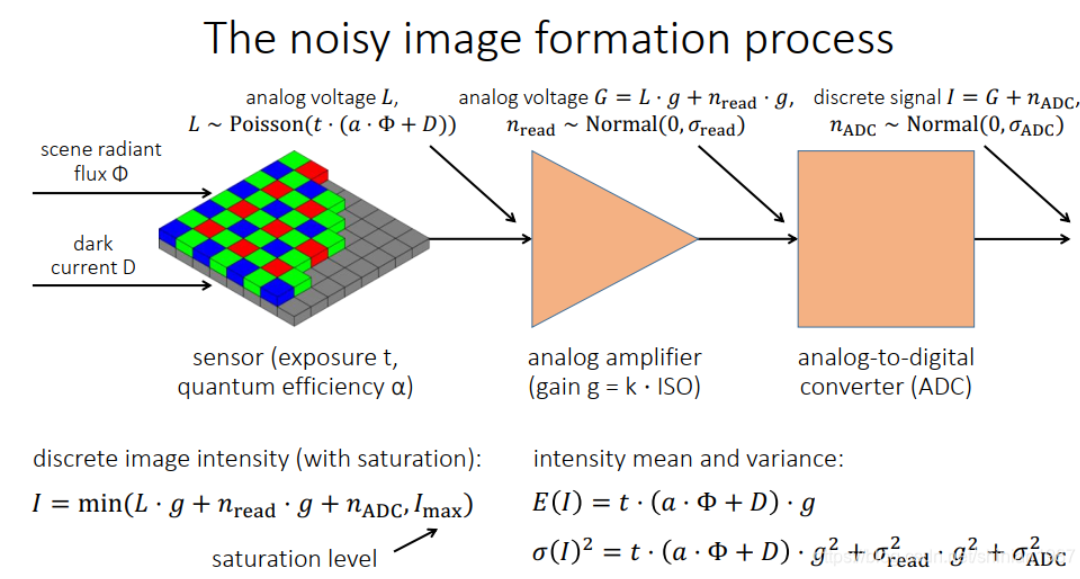
在 camera ISP 流程中,有一个 denoise 的环节,一般在 demosaic 后面,噪声一般是 sensor 接收光子然后转化成 RAW 图的过程中产生的,环境中的光通过镜头模组照射到 sensor 上,因为光电效应,会激发很多电子,这些电子转成电流被一个模拟放大器放大,然后通过一个 ADC 模数转换,最后输出离散的照度值。
噪声的产生主要集中在绿色区域部分,可以发现是在sensor端引入的,分别是光电转换,和AD转换
这里主要分成四种噪声
-
光子噪声(photon noise)、暗噪声(dark noise)
由于光激发电子的随机性,会产生 photon noise,也被称为光子散粒噪声(photon shot noise),而 sensor 本身由于发热激发的暗电流也会产生噪声,这种噪声称为 dark noise 或者热噪声
-
读入噪声(read noise)
模拟放大器在放大信号的时候,会产生噪声,这种噪声称为 read noise
-
模数转换噪声(analog-to-digital converters noise)
模数转换器在进行模数转换的时候,会产生噪声,这种噪声称为 ADC noise
1)光子噪声(photon noise)、暗噪声(dark noise)
photon noise 是和环境照度相关的一种噪声,假设环境照度为Φ,光电转换效率为α,曝光时间为 t ,则 photon noise 满足如下分布:
$$
n∼Poisson(Φ,α,t)=Poisson(Φ⋅α⋅t)
$$
dark noise 则和暗电流有关,和环境照度无关,曝光时间越长,电流导致 sensor 发热越大,产生的噪声也越多,假设暗电流强度为 D DD,曝光时间为 t tt, 则 dark noise 满足如下分布:
$$ n ∼ P o i s s o n ( D ⋅ t ) n \sim Poisson(D \cdot t) $$ poisson 分布是一种离散分布,满足如下的表达式: $$ N∼Poisson(λ)⇔P(N=k,λ)= \frac{λ^ke^{ −λ }}{k!} $$
poisson 分布的均值和方差都是λ
为什么 photon noise 和 dark noise 是满足泊松分布的呢:
这是因为光子是粒子,是一份一份的,而且环境中的光线照射到 sensor 上的时候,激发出来的电子并不是一个恒定的数量,而是会有波动,比如这一秒有 100 个,下一秒可能只有 90 个,这种波动导致 sensor 上每个 pixel 产生的电子数并不一样,而是满足一定的统计分布,这种统计分布符合泊松分布,所以 photon noise 满足泊松分布。
dark noise 也是一样的,sensor 温度升高之后,由于热效应激发的电子数也不是恒定的,而是离散随机的,也满足一种泊松分布。
由于激发的电子数由环境光照和暗电流共同决定,所以这个过程激发的总电子数满足如下的分布: $$ L=N_{photon−detection}+N_{phantom−detection} \
N_{photon−detection}∼Poisson(Φ⋅α⋅t) \
N_{phantom−detection}∼Poisson(D⋅t) \
L∼Poisson(t⋅(α⋅Φ+D))
$$
2)读入噪声(read noise)、ADC noise
光电转换之后,后面就是信号放大,利用一个模拟放大器,这个过程会引入 read noise,后面的 ADC 转换也会引入量化误差,产生噪声, read noise 和 ADC noise 都是加性噪声,并且都满足均值为 0 的高斯分布:
$$
n_{read}∼Normal(0,σ_{read}) \
n_{ADC}∼Normal(0,σ_{ADC})
$$
信号放大过程,就是把前面光电转换的电信号进行放大,放大系数是由电路系统本身决定的,也就是我们通常所说的 gain 值,这个值和 ISO 也有关系:
$$
g=k⋅ISO
$$
前面的电信号 L LL 经过放大之后,可以表示为 G, 这个过程引入的 read noise 也会被放大:
$$
G=L⋅g+n_{read}⋅g
$$
再经过后面的 ADC 转换,可以表示为:
$$
I=G+n_{ADC}
$$
所以最后的信号可以表示为:
$$
I=L⋅g+n_{read}⋅g+n_{ADC}
$$
我们可以算出这个信号I的均值为:
$$
E(I)=g⋅E(L)+g⋅E(n_{read})+E(n_{ADC})
$$
前面说过,因为 read noise 和 ADC noise 均值为 0, 所以上面的表达式最后可以简化成:
$$
E(I)=g⋅E(L)=g⋅t⋅(α⋅Φ+D)
$$
我们可以算出这个信号I的方差为:
$$
σ(I)^2=σ(L⋅g)^2+σ(n_{read}⋅g)^2+σ(n_{ADC})^2= g^2⋅t⋅(α⋅Φ+D)+g^2⋅σ(n_{read})^2 + σ(n_{ADC})^2
$$
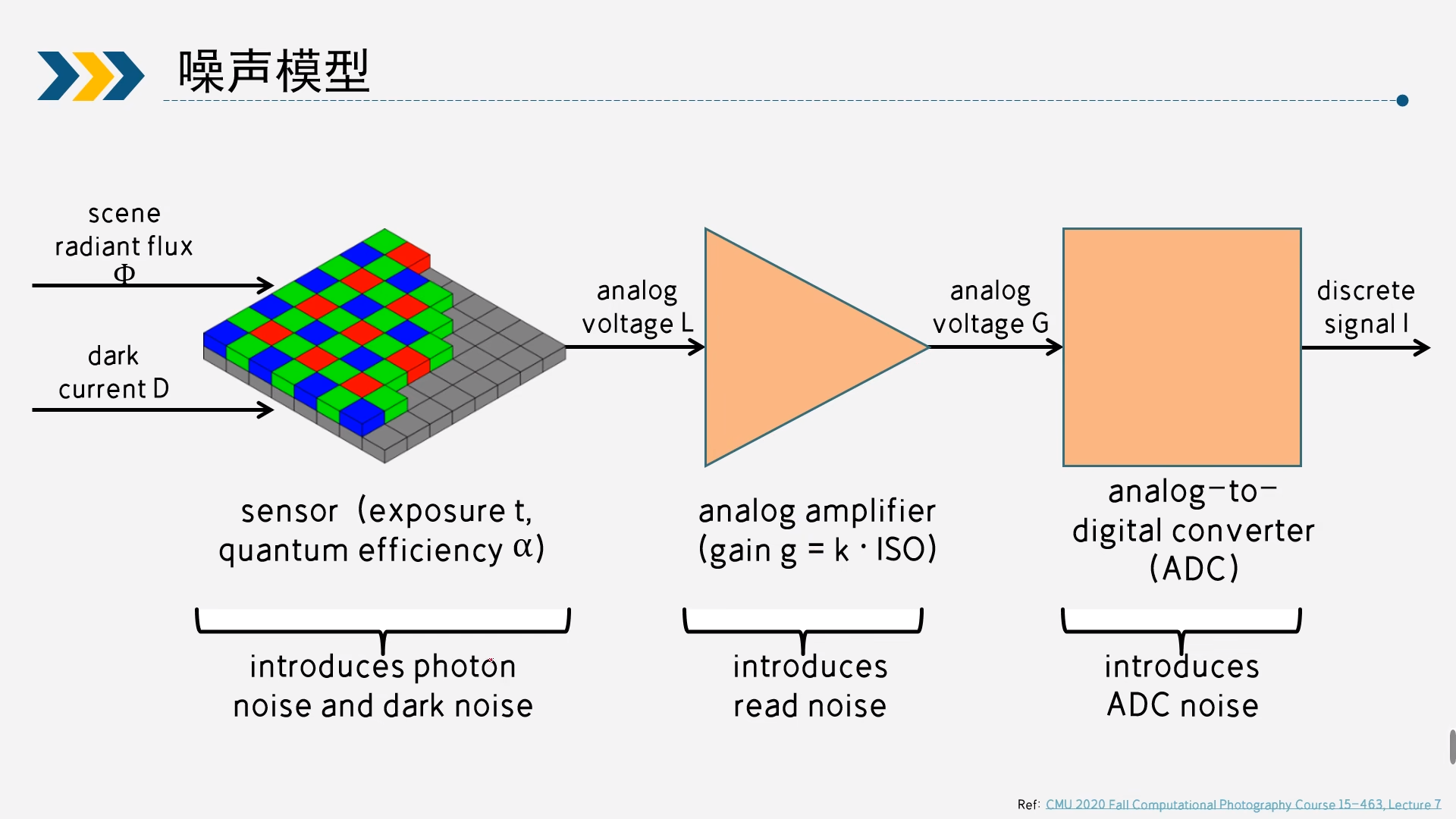
完整的过程如下所示:
因为 read noise 和 ADC noise 都是加性噪声,所以可以将两种噪声合并,进行化简:
$$
I=L⋅g+n_{add} \
n_{add}=n_{read}⋅g+n_{ADC}
$$
则上面信号的方差可以表示为:
$$
σ(I)^2=g^2⋅t⋅(α⋅Φ+D)+ σ(n_{add})^2
$$
从上面的表达式可以看出
photon noise
与环境光照
Φ有关,光照越强,photon noise 占主导dark noise
和 sensor 本身的热效应有关,曝光越长,dark noise 越大
read noise
和 ISO 有关,ISO 越高,read noise 越大
ADC noise
是 AD 本身的量化误差,和 ISO,环境亮度都没有关系
噪声的关系总结如下
| 方式 | 主噪声类别 | 标记 |
|---|---|---|
| 亮像素 | 光噪声 | 场景依赖 |
| 暗像素 | 读噪声和ADC噪声 | 非场景依赖 |
| 低ISO增益 | ADC噪声 | 增益后 |
| 高ISO增益 | 光噪声和读噪声 | 增益前 |
| 长曝光 | 暗噪声 | 热依赖 |
一般来说,在光照充足的区域,photon noise 占主导,而光线不足的区域,add noise 占主导。
Noise calibration降噪方法
1)算出暗电流D
为了进行降噪,需要对噪声模型的参数进行估计,上面噪声模型的参数包括暗电流 D,模拟放大系数 gain 值 g ,以及 read noise 和 ADC noise,根据上面信号的均值和方差,可以看出信号的均值和环境照度以及暗电流有关,如果环境照度为 0 ,则信号的均值就是和暗电流有关,通过这种方式,可以估计出 sensor 的暗电流产生的信号大小,所以估计暗电流,可以把相机镜头盖住,然后拍摄多帧图像,再进行平均,这样得到的平均值,就近似为暗电流的大小,不过注意这里还有一个 gain 值:
$$
E(I)=g⋅t⋅(α⋅0+D)=g⋅t⋅D
$$
不同的 ISO,会有不同的 gain 值,估计暗电流,也需要考虑不同的 gain 值的影响。
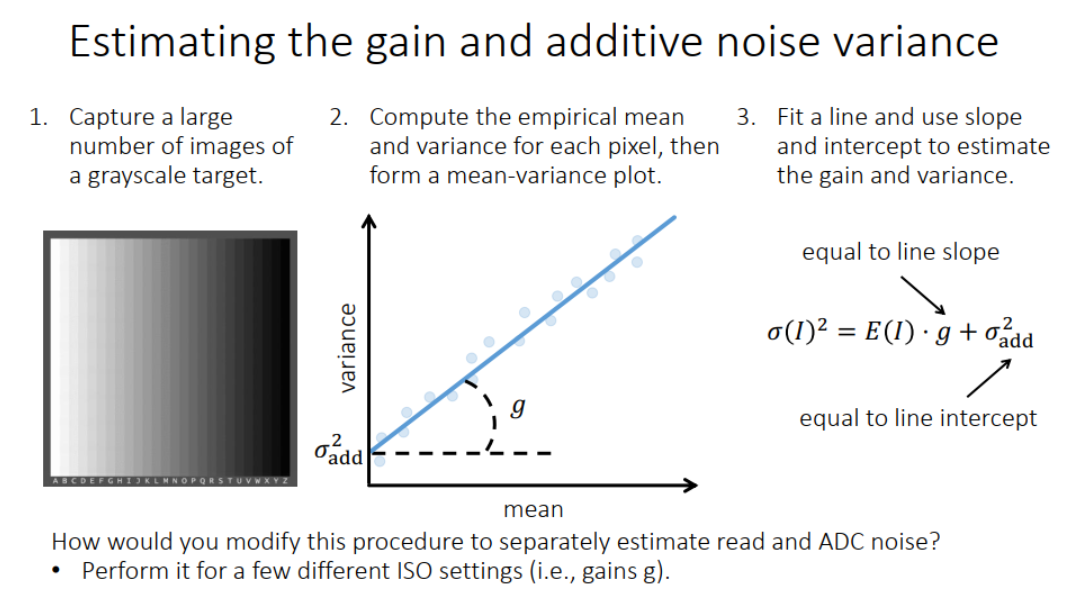
2)估计模拟放大系数 gain 值 g
一旦估计出暗电流,我们减去这部分信号,以消除暗电流的影响,剩下的就是估计模拟放大系数 gain 值,以及 read noise 和 ADC noise,这两者统称为加性噪声,可以表示为 add noise,一旦去除 D,信号的均值和方差可以表示为:
$$
E(I)=g⋅t⋅(α⋅Φ)\
σ(I)^2=g^2⋅t⋅(α⋅Φ)+σ(n_{add})^2 \
σ(I)^2=g⋅E(I)+σ(n_{add})^2
$$
从上式可以看出,信号的方差和均值满足一个线性关系,放大倍数就是 g,而截距就是加性噪声,所以一般可以通过拍摄多帧灰度图像,然后计算每个像素点的均值和方差,再做一个线性拟合,来估计gain 值 和加性噪声。
最后,重要的一点是这些估计都应该在 RAW 域进行,因为 RAW 域的信号才与环境光照满足线性关系。而 photon noise 是光电效应本身的随机属性,这个是没有办法消除的。
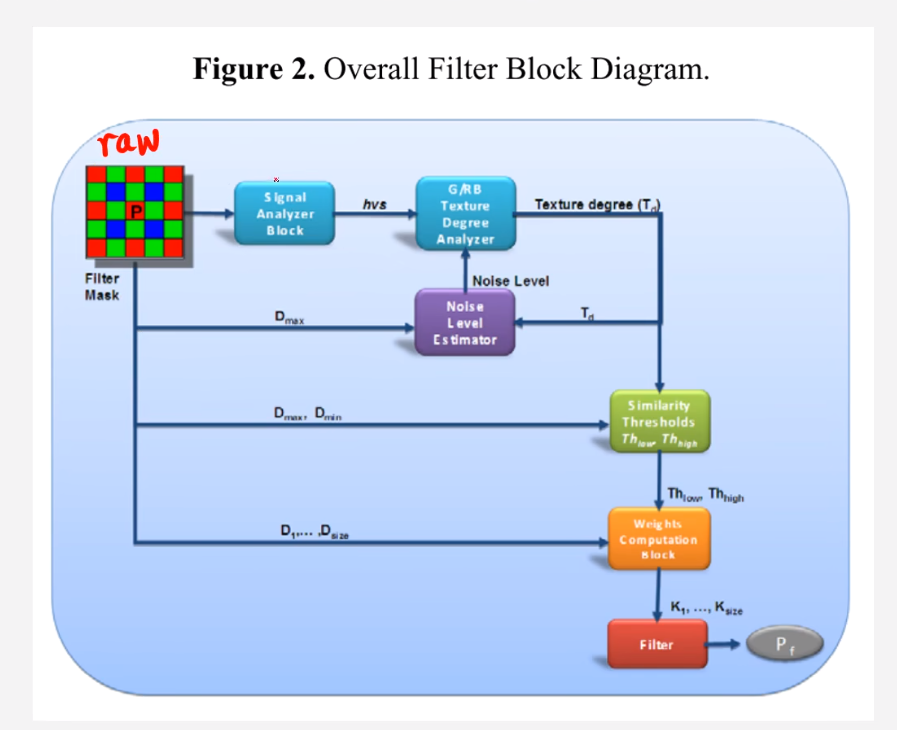
2.2.1.2噪声算法原理
该算法主要是通过如图的几个模块进行降噪,通过像素值的差来作为判断依据。下面将通过每个模块的单独讲解来介绍该方法。
2.2.1.2.1Signal Analyzer Block(主要为了计算HVS)
噪声在RAW上的分布符合高斯泊松分布,所以噪声随着亮度增加会变大。这里可能和常规的理解不太一样,我们一般说的是越暗噪声越大,这里是因为还有一个SNR的指标,人眼看到的噪声大小是通过SNR来体现的,所以亮度增加噪声变大,所以SNR会小,人眼就感觉噪声小而已。
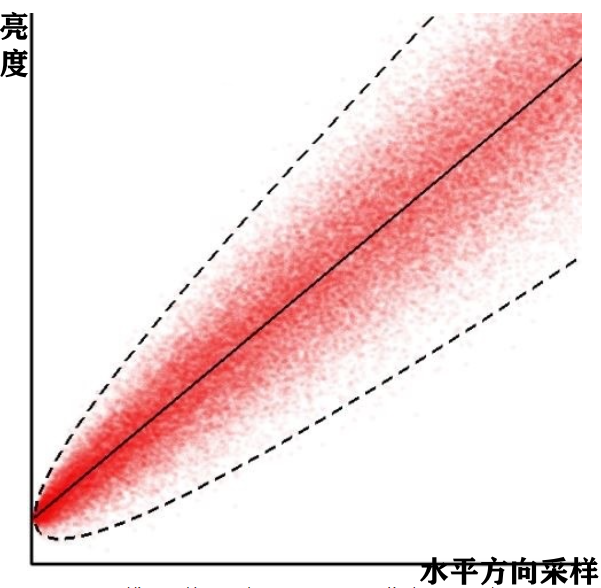
这个结论通常可以通过拍摄以上的连续灰阶卡来证明,拍摄N张以上的灰阶卡,然后从水平方向采样,将所有的采样信息通过绘制可以得到下面的分布
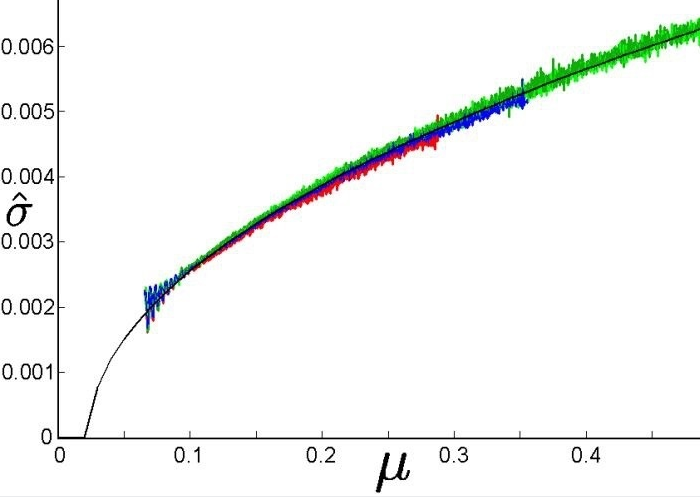
中间的黑色线就是均值,红色点就是实际像素值的分布,可以看出随着亮度变大,像素分布偏离中心均值的程度越大,也就是方差越大,从而说明噪声变大,SNR越小。这种变化趋势可以拟合成一下曲线
可以看出随着均值的变大,方差会变大,所以亮度越大降噪力度可以加大。
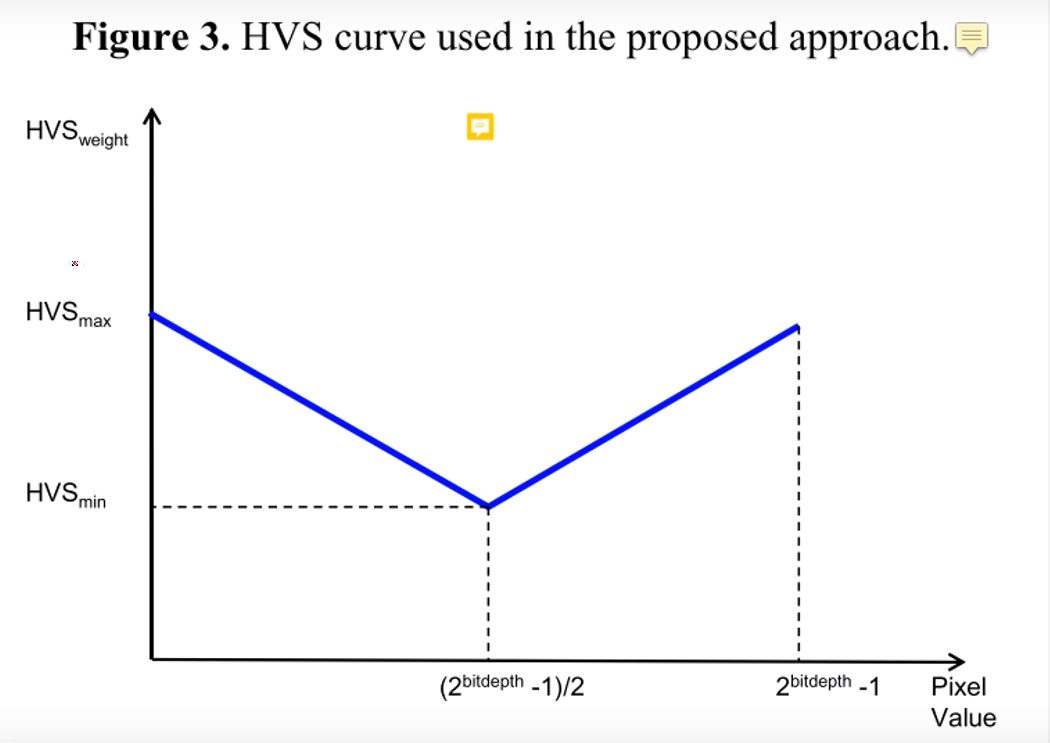
如上图是我们之前博客中提到的人眼亮度林敏度,越暗的区域,人眼对于亮度变化的灵敏度就越不敏感,所以对于暗部区域也可以提高降噪力度。 通过以上两个特性的分型,最终将降噪力度和亮度变化的关系定义为以下曲线
将中间亮度值对应的降噪力度设置为最小,然后两侧呈显现增长。
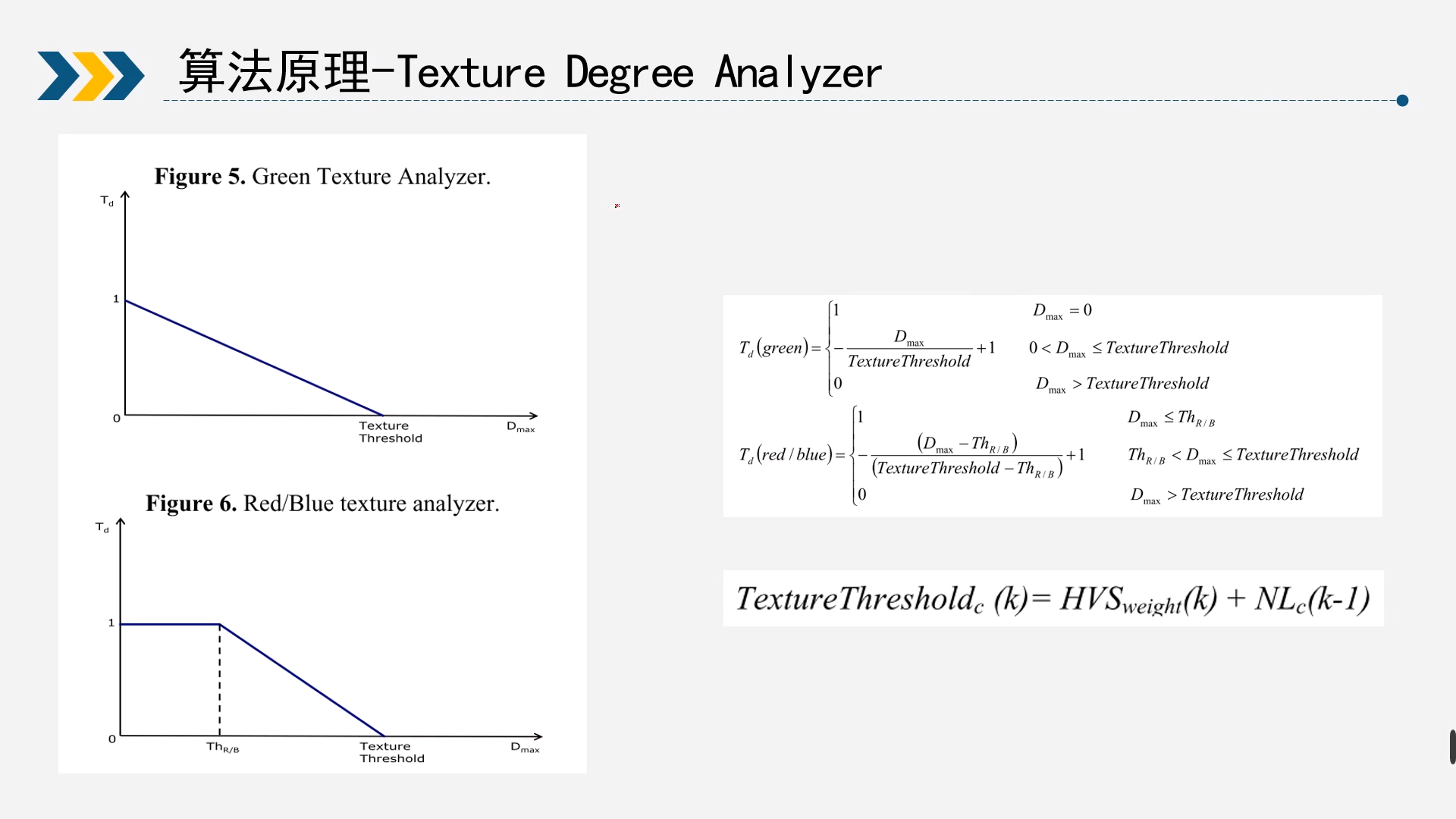
2.2.1.2.2Texture Degree Analyzer
该模块的主要功能就是通过上一个模块计算的HVS权重和下一个模块计算的noise level来判断平坦去和纹理区从而实现不同力度的降噪。 $$ TextureThreshold_c(k)=HVS_{weight}(k)+NL_c(k-1) $$ 首先通过以上公式计算出一个TextureThreshold,用于判断给定的降噪力度。因为noise level是下一个模块计算出来的,所以这里利用上一个像素点计算出来的noise level来预估当前的noise level,然后本次计算的noise level来预估下次,所以这里是一个循环迭代的过程,所以最开始的像素没有前一个像素的noise level的时候会设置一个初始值,这个值的选择就是调试时需要根据效果选择的了。
当计算除了TextureThreshold后,就根据邻域内像素点和中心像素值的差异(及D)来判断是否为平坦区。这里G通道和RB通道分开处理是因为人眼对G分量更为敏感,所以RB通道可以更多的维持在平坦区(即图中Td=1),如此后面就会加大平坦区的降噪力度,而因为人眼不敏感,所以RB通道牺牲更多的细节是在允许范围内的。当像素插值大于上面计算的TextureTheshold就认为的纹理区,那么就将Td设置为0。
2.2.1.2.3Noise Level Estimator
其中NL初始值为0.3
-
该模块用来评估噪声水平,设计时主要通过以下规则进行:
-
- 如果被判断为平坦区(Td=1),那么就将noise level设置为Dmax;
- 如果被判断为纹理区(Td=0),那么就将noise level保持为上一个像素的noise level;
- 若果介于平坦区和纹理去之间,那么就通过插值的方式计算出noise level。
$$
NL_R(k) = T_d(k)*D_{max}(k)+[1-T_d(k)]*NL_R(k-1) \
NL_G(k) = T_d(k)*D_{max}(k)+[1-T_d(k)]*NL_G(k-1) \
NL_B(k) = T_d(k)*D_{max}(k)+[1-T_d(k)]*NL_B(k-1)
$$
式中的NLR(k)代表当前像素点的nosie level, NLR(k-1)代表上一个像素的noise level,所以对于开始的像素没有上一个同通道的像素,那么就可以设置一个初始值。
2.2.1.2.4Similarity Thresholds and Weighting Coefficients computation
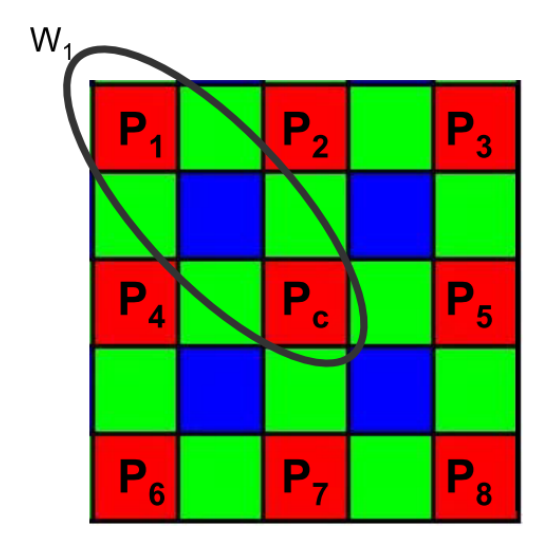
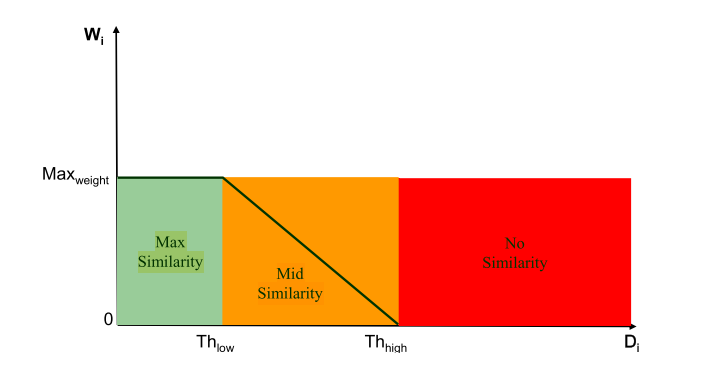
该模块主要计算各个点的权重值,如图为红色通道的权求解方式。利用周围像素与中心像素的差值来作为权重的最终判定依据。
$$
\begin{cases}
Th_{low}=Th_{high}=D_{max}&&if&T_d=1\
Th_{low}=D_{min}&&if&T_d=0\
Th_{high}=\frac{D_{min}+D_{max}}{2}&&if&T_d=0\
D_{min}<Th_{low}<Th_{high}&&if&0<T_d<1\
\frac{D_{min}+D_{max}}{2}<Th_{high}<D_{max}&&if&0<T_d<1\
\end{cases}
$$
首先通过计算的像素值差异求出一个Thlow和THhigh。
随后通过比较每个点的像素差异和这两个阈值的差异来给定权重。低于最低阈值说明像素差异很想,在滤波时的贡献应该大,需要给一个大的权重,相反差异太大就不应该对滤波提供大的贡献,所以需要将权重设置小,所以通过如上的一个分段线性的方式来给每个像素点分配权重。 $$ P_f=\frac{1}{N}\sum^{N}_{i=1}{[W_iP_i+(1-W_i)P_c]} $$ 最后通过上述公式完成滤波和归一化即可得到最终降噪后的像素值。
3算法
3.1PCA算法
3.2HVS算法
1close all;
2clear all;
3clc;
4
5%% --------------parameters set---------------------------------
6neighborhood_size = 5;
7initial_noise_level = 30;
8hvs_min = 5;
9hvs_max = 10;
10threshold_red_blue = 12;
11BayerFormat = 'RGGB';
12
13%% ----------------preparatory procedure------------------------
14% get org image
15% 通过降采样获取raw图
16addpath('../publicFunction');
17org_img = imread('images/kodak_fence.tif');
18double_img = double(org_img);
19[h, w, c] = size(double_img);
20figure();
21imshow(org_img);
22title('org image');
23
24% rgb2raw
25rggb_raw = RGB2Raw('../BNR/images/kodak_fence.tif', BayerFormat);
26figure();
27imshow(rggb_raw,[]);
28title('raw');
29
30% add noise to raw
31%使用了高斯的加性噪声
32noise_add = 10*randn(h, w);
33noise_raw = rggb_raw + noise_add;
34noise_raw(noise_raw<0) = 0;
35noise_raw(noise_raw>255) = 255;
36figure();
37imshow(noise_raw,[]);
38title('noise raw');
39
40%% -------------Denoise-----------------------------------------
41% pad raw
42%对图形边界进行扩充
43pixel_pad = floor(neighborhood_size / 2);
44pad_raw = expandRaw(noise_raw, pixel_pad);
45
46denoised_out = zeros(h, w);
47% texture_degree_debug = zeros(h, w);
48
49for i = pixel_pad+1: h+pixel_pad
50 for j = pixel_pad+1: w+pixel_pad
51 % center pixel(获取中心像素)
52 center_pixel = pad_raw(i, j);
53
54 % signal analyzer block(求得HVS权重)
55 half_max = floor(255 / 2);
56 if center_pixel <= half_max
57 hvs_weight = -(((hvs_max - hvs_min) * double(center_pixel)) / half_max) + hvs_max;
58 else
59 hvs_weight = (((center_pixel - 255) * (hvs_max - hvs_min)) / (255 - half_max)) + hvs_max;
60 end
61
62 % noise level estimator previous value
63 if j < (2*pixel_pad + 1)
64 %像素初始值30
65 noise_level_previous_red = initial_noise_level;
66 noise_level_previous_blue = initial_noise_level;
67 noise_level_previous_green = initial_noise_level;
68 else
69 %根据上面的NL值计算下一个NL值
70 noise_level_previous_green = noise_level_current_green;
71 if mod(i, 2) ~= 0 % red
72 noise_level_previous_red = noise_level_current_red;
73 elseif mod(i, 2) == 0 % blue
74 noise_level_previous_blue = noise_level_current_blue;
75 end
76 end
77
78 % Processings depending on Green or Red/Blue
79
80 neighborhood = [pad_raw(i - 2, j - 2), pad_raw(i - 2, j), pad_raw(i - 2, j + 2), ...
81 pad_raw(i, j - 2), pad_raw(i, j + 2), ...
82 pad_raw(i + 2, j - 2), pad_raw(i + 2, j), pad_raw(i + 2, j + 2)];
83 d = abs(neighborhood - center_pixel);
84 d_max = max(d);
85 d_min = min(d);
86 % Red channel
87 if mod(i, 2) == 1 && mod(j, 2) == 1
88 % calculate texture_threshold
89 texture_threshold = hvs_weight + noise_level_previous_red;
90
91 % texture degree analyzer
92 if (d_max <= threshold_red_blue)
93 texture_degree = 1;
94 elseif ((d_max > threshold_red_blue) && (d_max <= texture_threshold))
95 texture_degree = -((d_max - threshold_red_blue) / (texture_threshold - threshold_red_blue)) + 1;
96 elseif (d_max > texture_threshold)
97 texture_degree = 0;
98 end
99
100 % noise level estimator update
101 noise_level_current_red = texture_degree * d_max + (1 - texture_degree) * noise_level_previous_red;
102
103 % Blue channel
104 elseif mod(i, 2) == 0 && mod(j, 2) == 0
105 texture_threshold = hvs_weight + noise_level_previous_blue;
106 % texture degree analyzer
107 if (d_max <= threshold_red_blue)
108 texture_degree = 1;
109 elseif ((d_max > threshold_red_blue) && (d_max <= texture_threshold))
110 texture_degree = -((d_max - threshold_red_blue) / (texture_threshold - threshold_red_blue)) + 1;
111 elseif (d_max > texture_threshold)
112 texture_degree = 0;
113 end
114
115 % noise level estimator update
116 noise_level_current_blue = texture_degree * d_max + (1 - texture_degree) * noise_level_previous_blue;
117 % Green channel
118 else
119 texture_threshold = hvs_weight + noise_level_previous_green;
120 % texture degree analyzer
121 if (d_max == 0)
122 texture_degree = 1;
123 elseif ((d_max > 0) && (d_max <= texture_threshold))
124 texture_degree = -(d_max / texture_threshold) + 1;
125 elseif (d_max > texture_threshold)
126 texture_degree = 0;
127 end
128
129 % noise level estimator update
130 noise_level_current_green = texture_degree * d_max + (1 - texture_degree) * noise_level_previous_green;
131
132 end
133 % similarity threshold calculation
134 if (texture_degree == 1)
135 threshold_low = d_max;
136 threshold_high = d_max;
137 elseif (texture_degree == 0)
138 threshold_low = d_min;
139 threshold_high = (d_max + d_min) / 2;
140 elseif ((texture_degree > 0) && (texture_degree < 1))
141 threshold_high = (d_max + ((d_max + d_min) / 2)) / 2;
142 threshold_low = (d_min + threshold_high) / 2;
143 end
144
145 % weight computation
146 size_d = size(d);
147 length_d = size_d(2);
148 weight = zeros(size(d));
149 pf = 0;
150 for w_i = 1: length_d
151 if (d(w_i) <= threshold_low)
152 weight(w_i) = 1;
153 elseif (d(w_i) > threshold_high)
154 weight(w_i) = 0;
155 elseif ((d(w_i) > threshold_low) && (d(w_i) < threshold_high))
156 weight(w_i) = 1 + ((d(w_i) - threshold_low) / (threshold_low - threshold_high));
157 end
158 pf = pf + weight(w_i) * neighborhood(w_i)+ (1 - weight(w_i)) * center_pixel;
159 end
160 denoised_out(i - pixel_pad, j - pixel_pad) = pf / length_d;
161 end
162end
163figure();imshow(uint8(denoised_out),[]);title('denoise');
164figure();imshow((noise_raw-rggb_raw), []);title('noise');
165figure();imshow((denoised_out-rggb_raw), []);title('noise reduced');
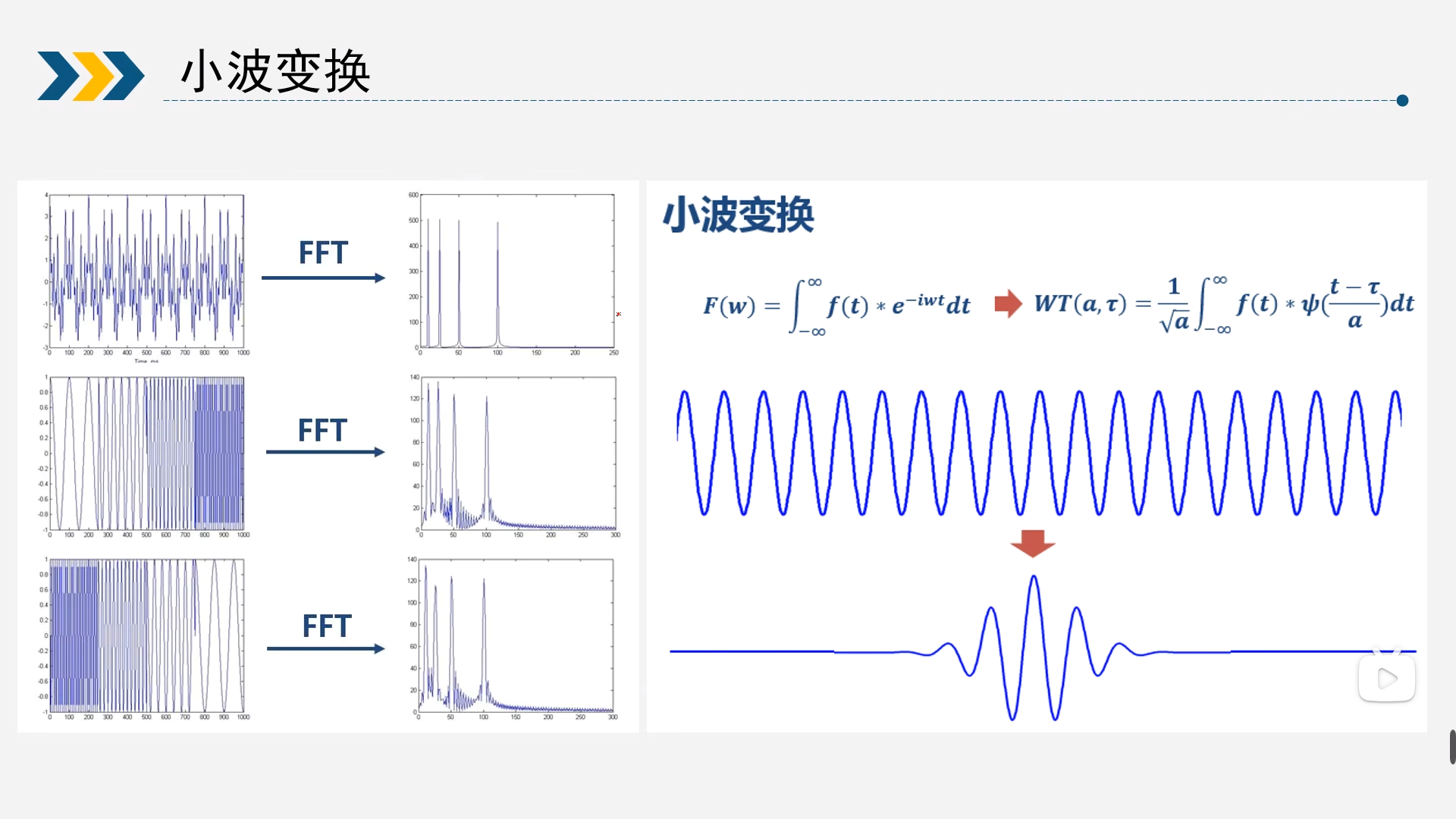
4小波降噪
小波降噪理论:
图像的能量主要集中在低分辨率子带上,而噪声信号的能量主要分布在各个高频子带上。
原始图像信息的小波系数绝对值较大,噪声信息小波系数的绝对值较小。
参考
本文对应的论文,点击这里
- Noise reduction for CFA image Sensors exploiting HVS behaviour - Bosco et al. - 2009
- PCA_Based Spatially Adaptive Denoising of CFA Images for Single-Sensor Digital Cameras
- PSEUDO FOUR-CHANNEL IMAGE DENOISING FOR NOISY CFA RAW DATA Hiroki Akiyama , Masayuki Tanaka , and Masatoshi Okutomi Tokyo Institute of T