本文是isp算法学习的第九篇章，主要是讲述NR原理和算法。

人类的世界就是一个信号传输的世界，所以噪声无处不在，图像作为一种信号传输的方式当然也无法幸免。为了尽量减少噪声对图像质量的影响，还原物体的本来状态就提出了一系列降噪的方法，本文就简单介绍几种常见的降噪滤波算法。

1产生原因

噪声原因

1.1图像获取过程中

由于受传感器材料属性、工作环境、电子元器件和电路结构等影响，会引入各种噪声，如电阻引起的热噪声、场效应管的沟道热噪声、电子噪声、暗电流噪声、光响应非均匀性噪声。

1.2信号传输过程中

由于传输介质和记录设备等的不完善，数字图像在其传输记录过程中往往受到各种噪声的污染，在图像处理的某些环节当输入的对象并不如预想时也会在结果图像中引入噪声。

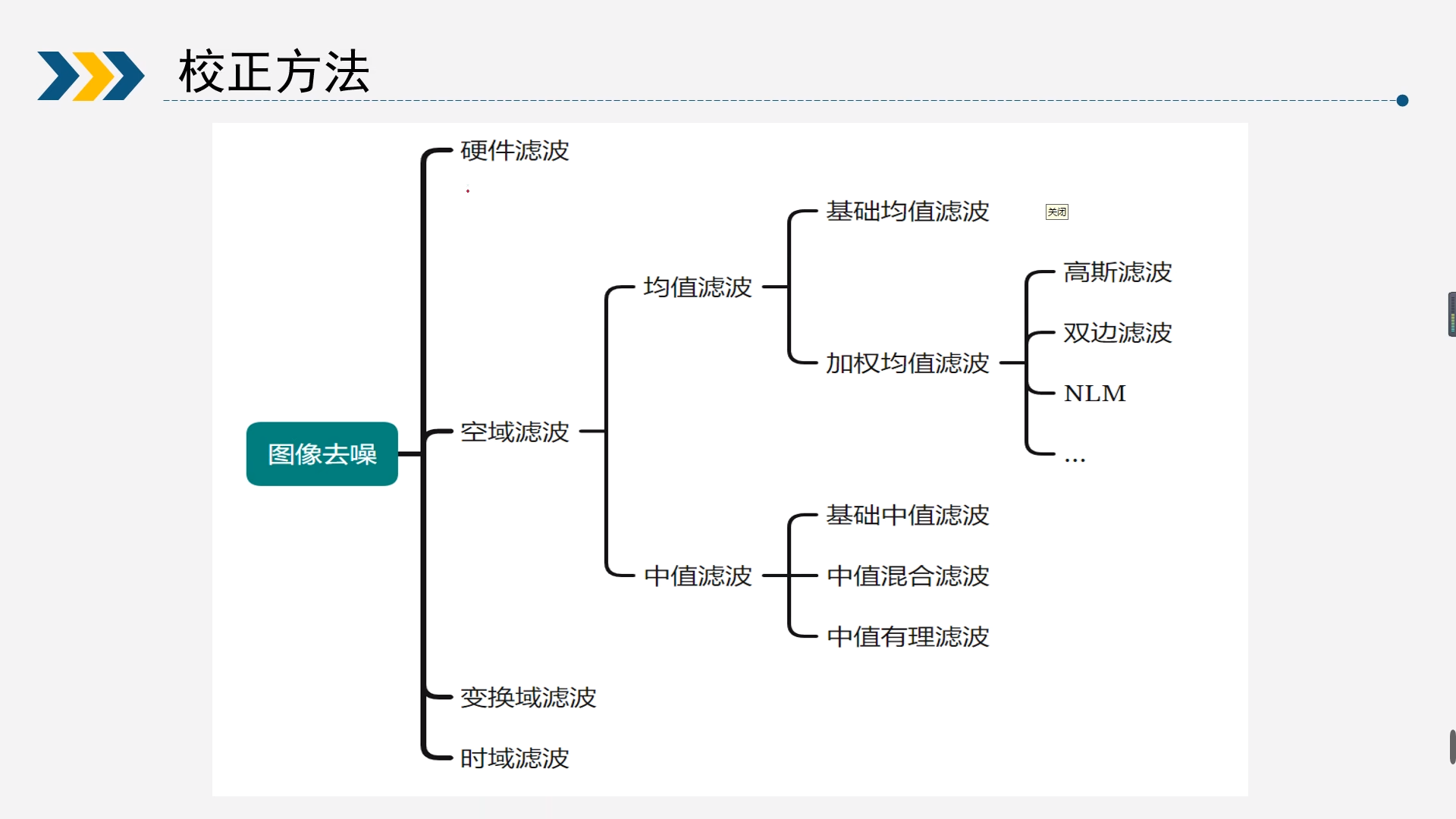
2校正方法

图像去噪的算法大致分位这么几类，包括硬件去噪，从源头降低噪声，常见的方式有CDS(cor related double sampling)，但是这种硬件的方式不是ISP涉及的范围所以不做过多介绍。

大致分位空域滤波、变换域滤波和时域滤波，当然还有一些其他方式比如空域和变换域相结合的方式

2.1空域滤波-均值滤波

2.1.1均值滤波

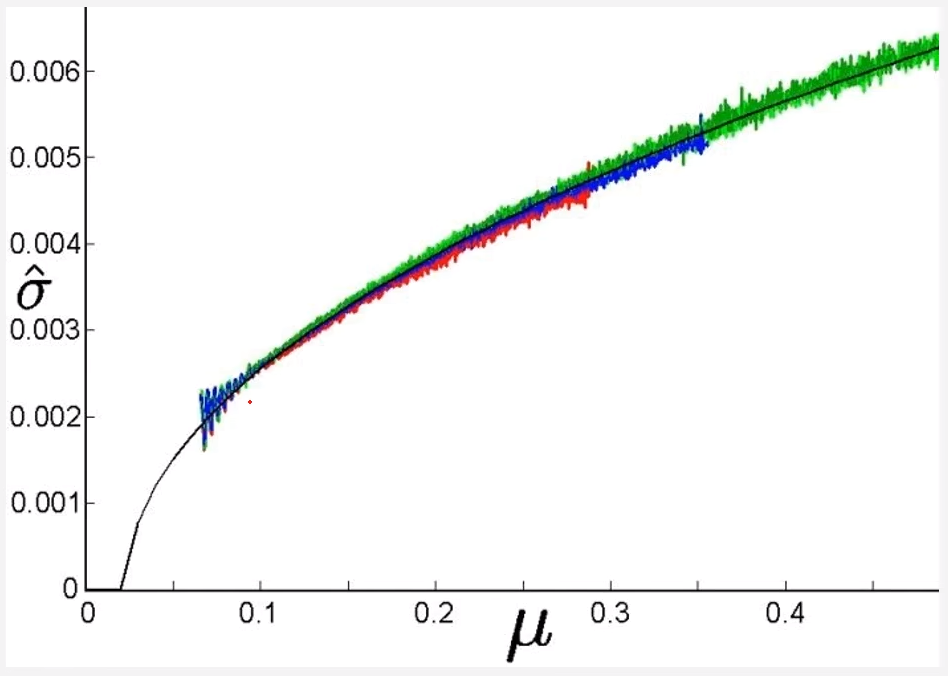
如图是一个信号和噪声的分布图像，黑色曲线是真实信号，彩色的是多次采集的信号，会发现采集的信号是在真实信号上下波动，这个波动就是噪声对信号带来的影响。

最早为了消除这种噪声有人就提出采用多张同一场景的图片求和取平均来消除，因为噪声是随机的，每张图中的噪声使得信号的偏移是不固定的，多次求平均后就能使得信号接近真实信号。

就像上图中，对彩色的信号求平均相当于黑色曲线上下的值求平均，结果自然就接近黑色曲线从而达到去噪的效果。从多张叠加求平均的想法中有人就提出了从一张图里求平均来到达降噪的效果，也就是这里提到的均值滤波。

其实整个算法的思想很简单，就是假设图像在一个很小的邻域范围内像素的变化不会太大，那么就可以在一个很小的邻域范围内求一个平均值来取代当前的像素值从而达到降噪的效果。

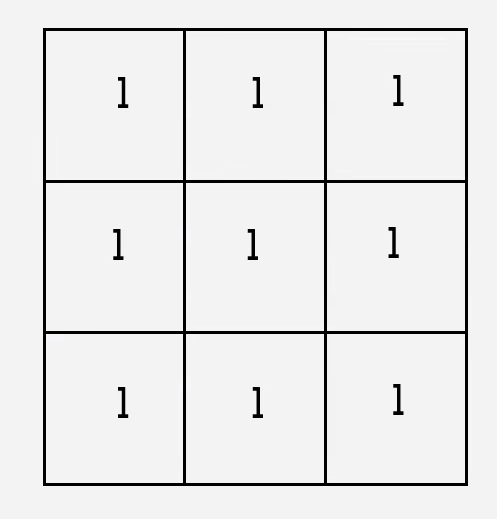
典型的应用就是在图像中取一个3X3的邻域，然后每个像素给权重1，最后求和取平均。然后让这个邻域遍历整个图像。

公式如下： $$ f(i, j) = \frac{1}{9} * [f(i-1, j-1)+f(i-1, j)+f(i-1, j+1)+f(i, j-1)+f(i, j)+f(i, j+1)+f(i+1, j-1)+f(i+1, j)+f(i+1, j+1))] $$

2.1.2高斯滤波

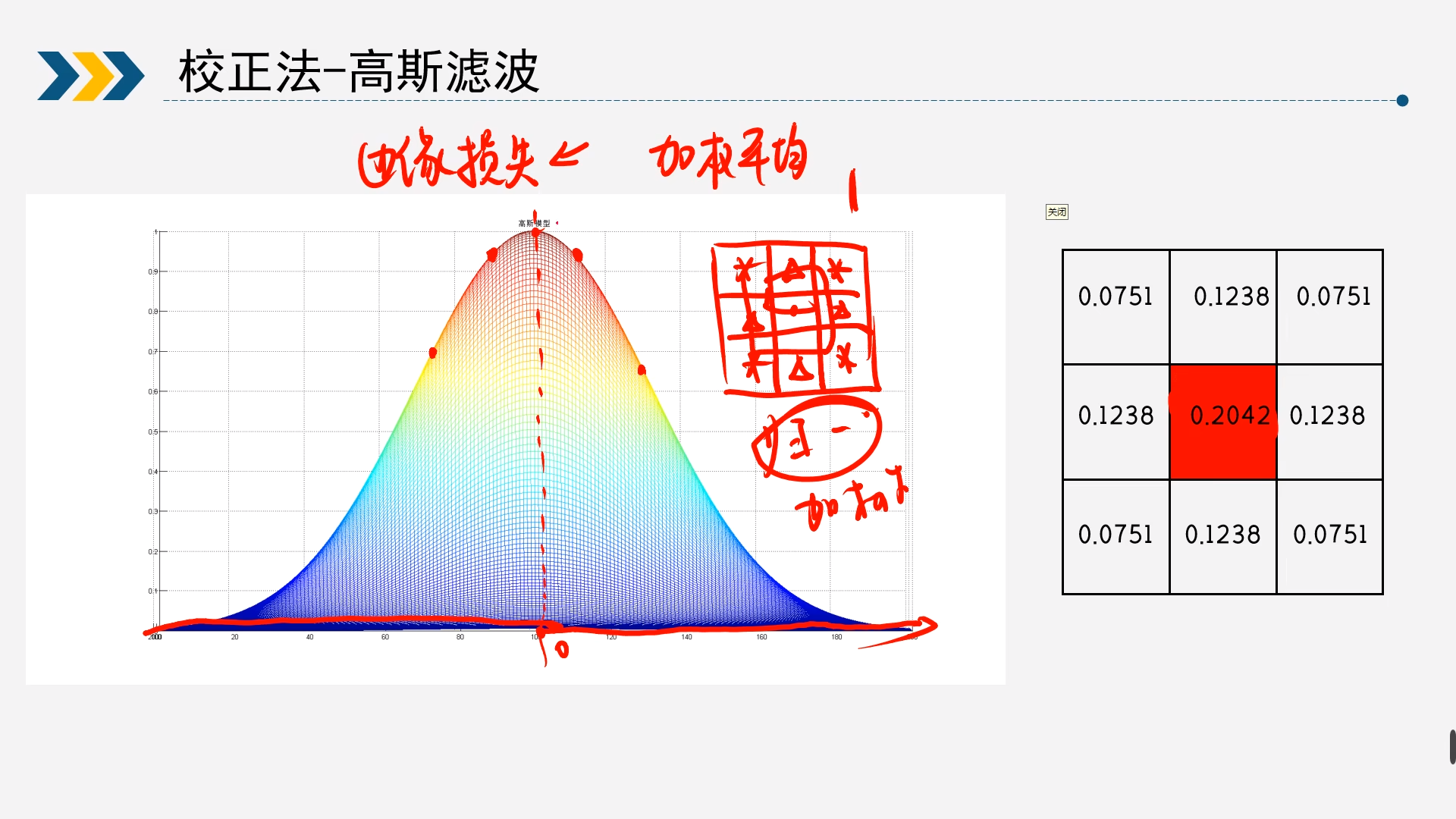
为了更好的保留边缘信息，就提出了加权平均的方法，就是平均之前每每个数的权重不一样。

其实在图形中更好理解，某一个点的值肯定和本身的像素值关系最大，所以对应的本身哪个点的权重就会更大些，我么通过以下公式计算 $$ \begin{aligned} f(i, j)& = \frac{1}{16} * [f(i-1, j-1) *1 +f(i-1, j) * 2+f(i-1, j+1)*1\& +f(i, j-1)*2+f(i, j)*4+f(i, j+1)*2\& +f(i+1, j-1)*1+f(i+1, j)*2+f(i+1, j+1)*1)] \end{aligned} $$ 上面这幅图就是典型的高斯分布的图像，自然中很多分布都是满足高斯分布的，那么如果噪声也是高斯分布我们就可以通过高斯分布来进行加权。高斯滤波的具体思路如下：

使用与中心像素的距离，通过高斯函数来计算该点的权重；
将所有点的权重求出来后对权重进行归一化处理；
利用加权平均的方式计算滤波后的像素值；
邻域窗口遍历图像，重复上述操作。

整体思路和均值滤波没有太大区别，这里代码实现就不做过多叙述。

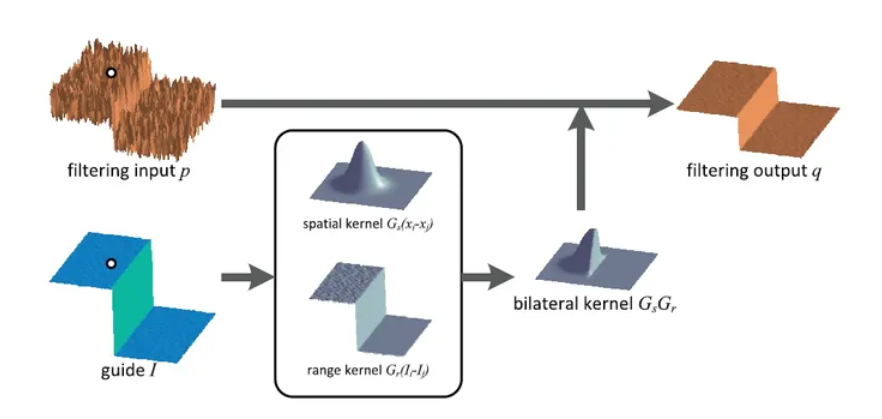
2.1.3双边滤波

虽然高斯滤波相对于普通均值滤波而言性能有所提升，但是依然对边缘滤波严重，为了进一步保留边缘信息，就需要对边缘做进一步处理。

于是就有人提出在高斯分布的基础上再加一个权重，这个权重和像素值的差别挂上联系，这个算法就是双边滤波算法。

如图是原始论文中的公式，从中可以看出双边滤波有两个高斯权重叠加而来。前面||p-q||就是高斯滤波中使用的距离权重，后面的|Ip-Iq|就是像素值的高斯分布的权重。

去噪的时候肯定需要相似的区域有更大的贡献，不相同的给小的权重
对于边缘而言，那么两侧的像素值的差距肯定很大，也就会导致离边缘另一侧不同的会分配一个小权重
同侧相差小就会有一个很大的权重，这样就不会由于取平均的时候将边缘两侧的大差异变小导致边缘变弱了，从而起到保留边缘的目的。

如图是双边滤波的示意图，当对白点位置进行滤波操作的时候，同侧像素差别较小会有一个大权重，而另一侧差别很大权重也就很小，二者结合后就相当于高斯滤波取一侧，然后利用这个核进行滤波操作。

2.1.4NLM（non-local mean）

这个是一种非局部均值算法。

前面的几种都是在邻域范围内对局部图像进行平均滤波，NLM则是利用整个图像的信息来进行降噪滤波处理。

对于p点而言，q1和q2点所在的邻域和p所在的邻域更相似，那么就给q1和q2较大的权重，而q3邻域和p邻域差别较大，就赋予一个较小的权重。具体权重的赋予方式其实也是高斯的一种方式，只不过e的对数是通过邻域简单欧拉距离来计算。

$$ w(i,j)=\frac{1}{Z(i)}e ^{-\frac{||v(N_i-v(N_j))||_2^2,a}{h^2}}\
Z(i)=\sum_je^{-\frac{||v(N_i-v(N_j))||_2^2,a}{h^2}} $$

相当于求了几邻域中对应位置像素差的平方和来当作分配权重的依据。当邻域相似时，这个方差就小，权重也就大，而差异很大时方差就很大，权重也就很小，满足了算法的需求。理论上每一个点进行去噪的时候会利用整个图像的信息来计算，但是为了降低运算量，一般不会用整个图像的信息来计算，而是在整个图像中先选择一个大的范围，然后用这个范围内的点的信息进行降噪处理。

具体算法思路如下：

遍历整幅图像；
针对每一个点定义一个滑动窗口，降噪的时候利用该窗口中的所有点的信息计算；
定义一个邻域范围，用来计算像素块的差异；
遍历滑动窗口中的点，求每个点的邻域范围和当前点的邻域范围的像素差值的平方和，并利用该值计算一个权重；
遍历完滑动窗口中的所有点后，滑动窗口中的每个点都有一个权重，对权重进行归一化处理；
得到归一化处理后的权重通过加权平均的方式计算出当前点的新的像素值；

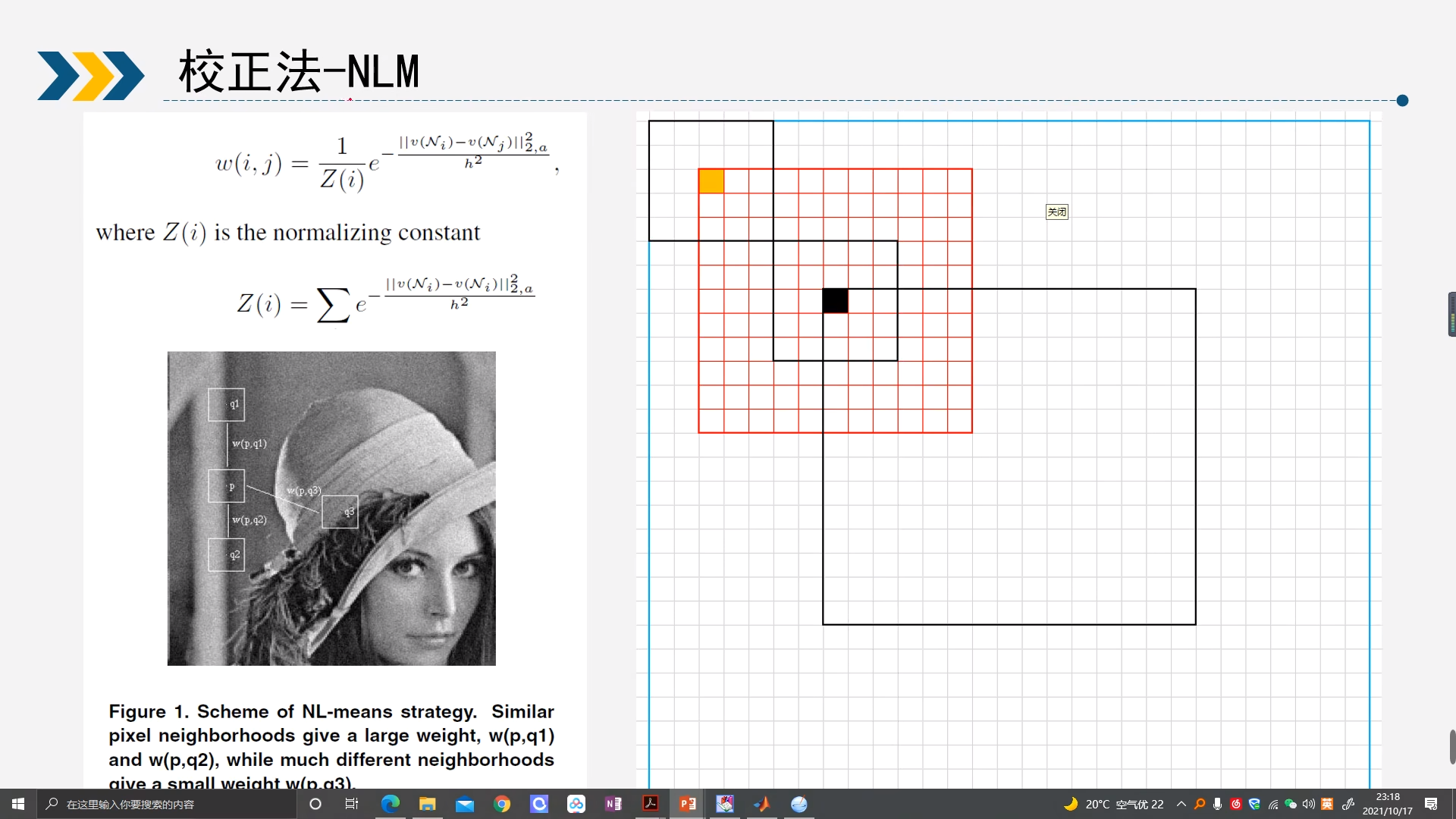
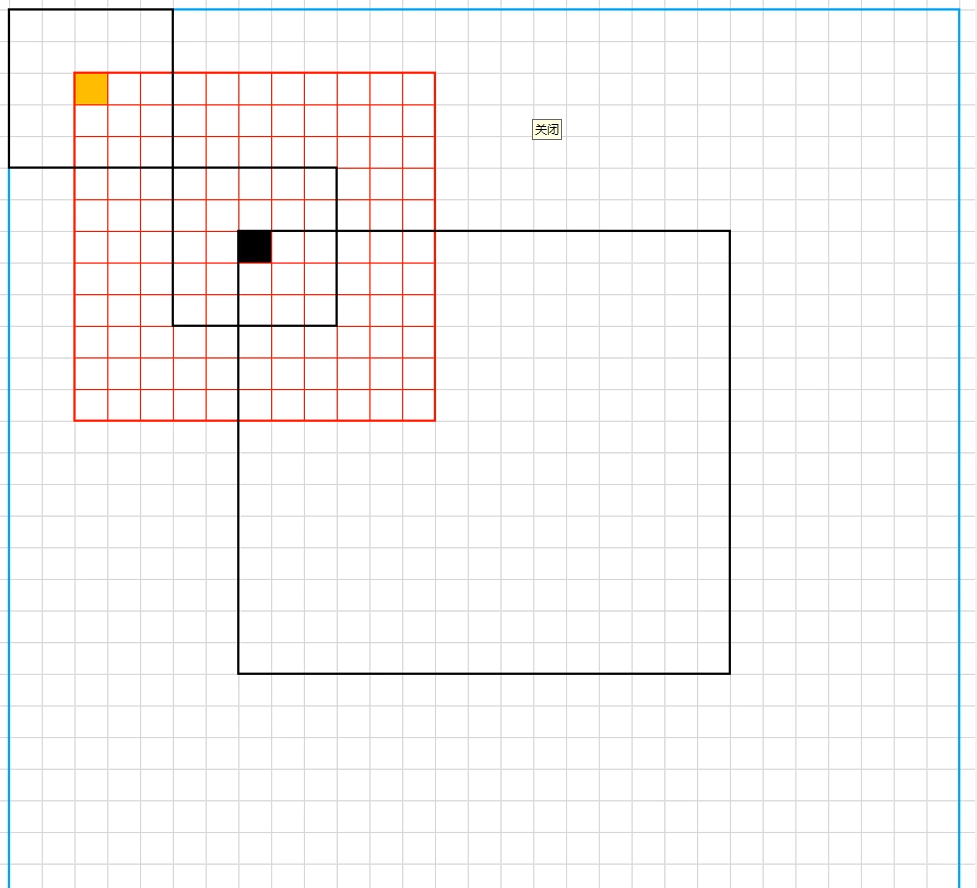
简化为图形就是如图的方式，最中间的黑色框的范围就是实际图像大小，外面蓝色范围时为扩充的图像（为了处理边缘领域不够的问题）。

计算黑色点的时候，就是定义一个红色框，然后黄色点在红色框中遍历，每次都计算出两个小黑色框对应位置像素的差值的平方从而求出一个权重，当红色框遍历完了之后对权重机型归一化，然后加权平均就能求出黑色点的值。

接着黑色点在图像中遍历，同时红色框随着黑点移动，然后黄色点又在红色框中移动，以此循环即可完成整幅图像的去噪操作。

2.2空域滤波-中值滤波

均值滤波作为一种线性滤波器，在滤除噪声的同时也会导致边缘模糊问题。而且均值滤波对高斯噪声的效果很好，但是对于椒盐噪声的效果就很一般。

但是中值滤波作为一种顺序滤波器，对于椒盐噪声的效果很好，而且保边能力很强

2.2.1中值滤波

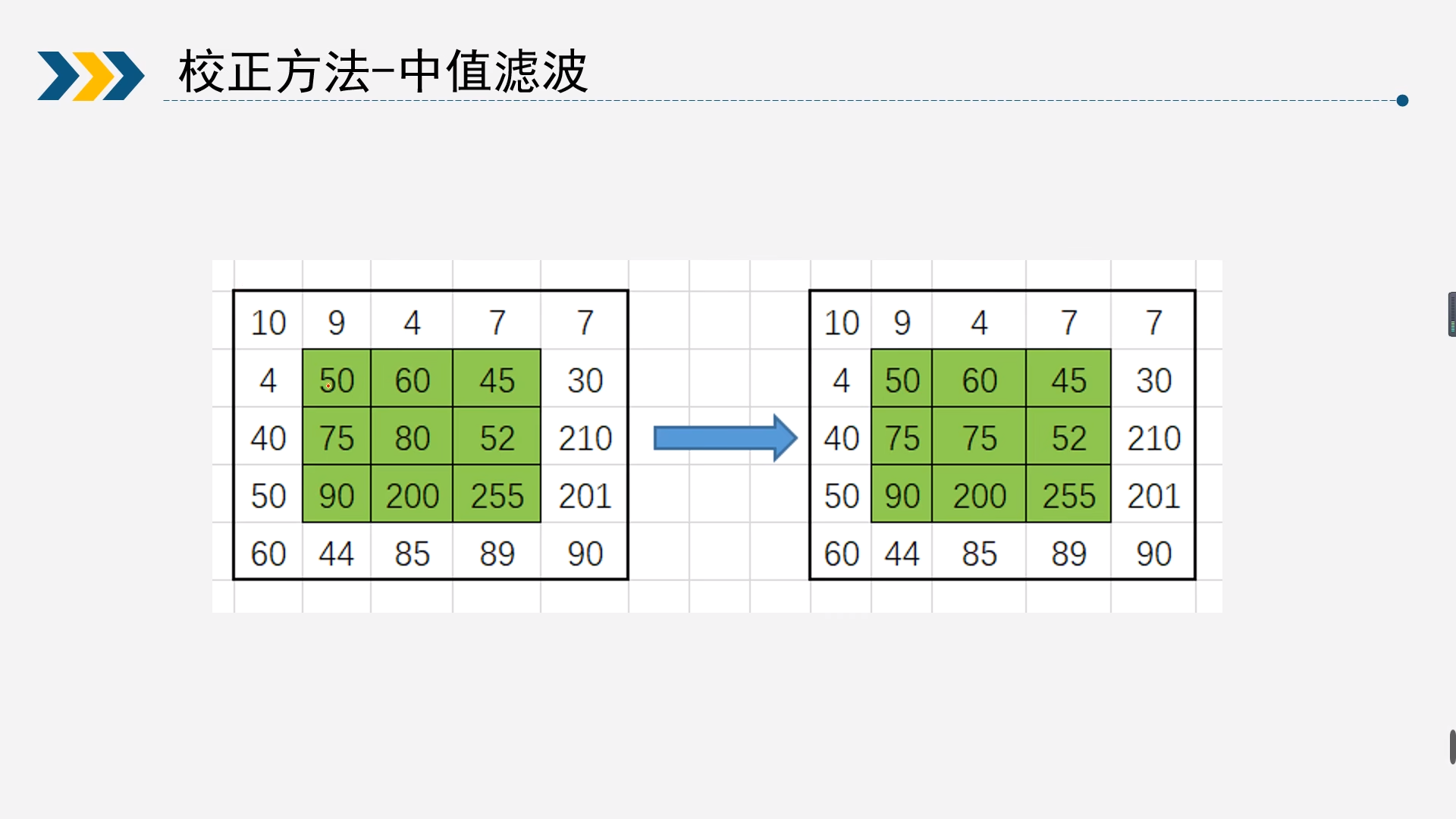
中值滤波很好理解，均值滤波就是在一个小窗口中求均值来取代当前像素值，而中值滤波就是通过求小窗口中的中位值来取代当前位置的方式来滤波。

如图绿色窗口就是当前的滤波窗口，在一个3X3的邻域窗口中进行滤波。那么中值滤波做的就是：

对这个邻域中的像素值进行排序：[45, 50, 52, 60, 75, 80, 90, 200, 255];
从排序后的数据中找出中位值：75；
用中位值取代当前位置的像素值，所以就可以得到右侧的滤波后的数据。

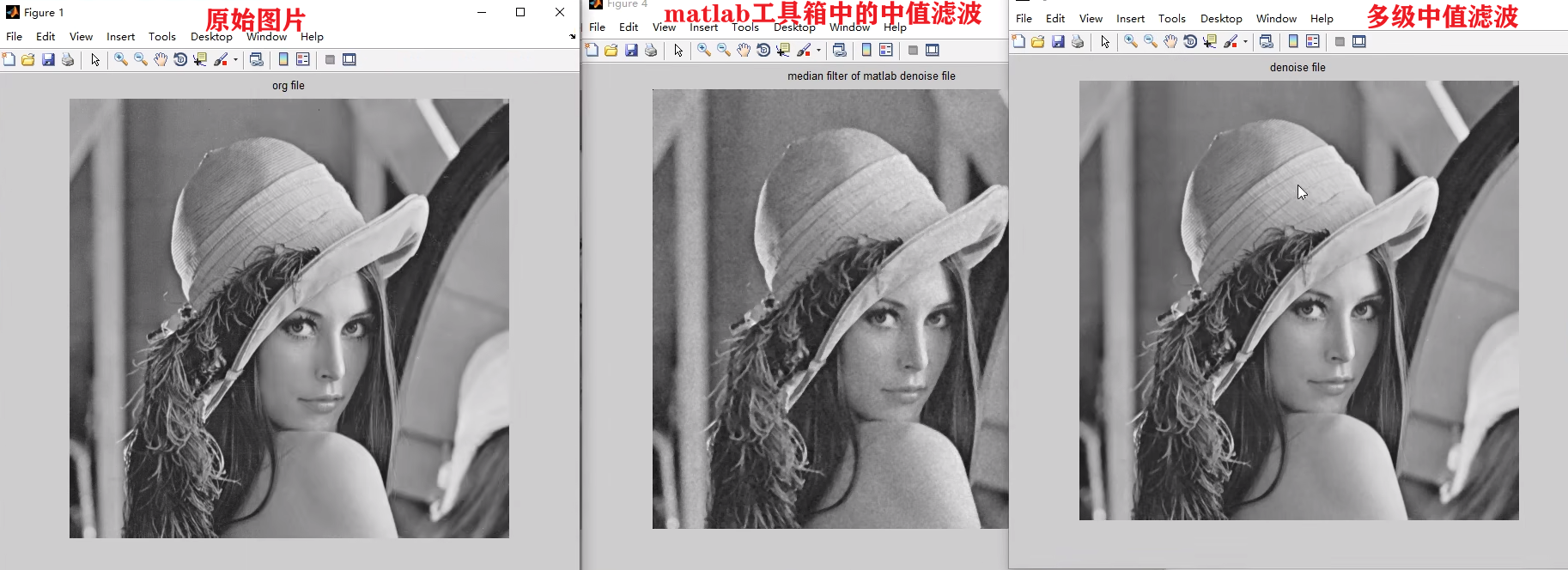
2.2.2多级中值滤波

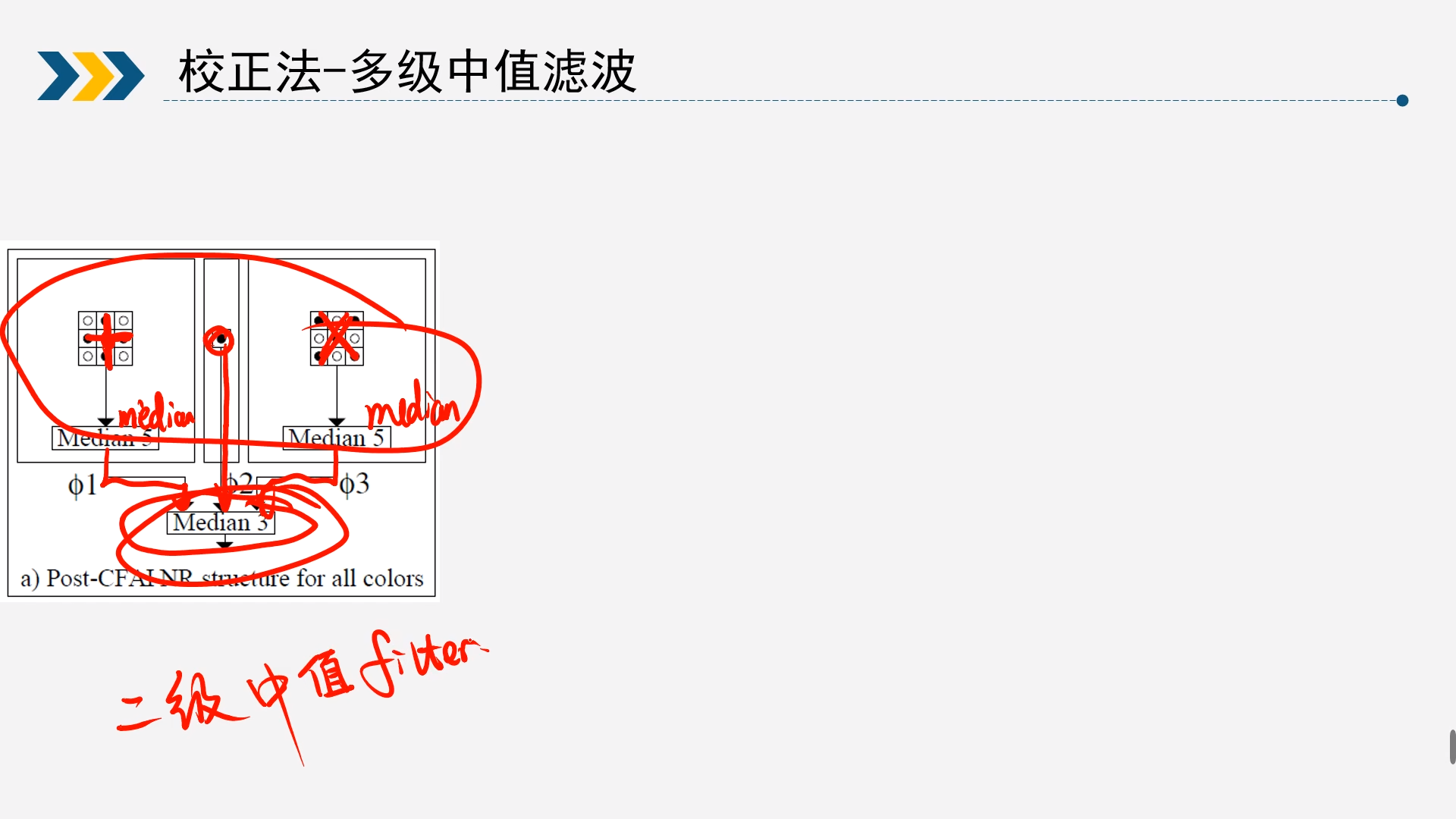
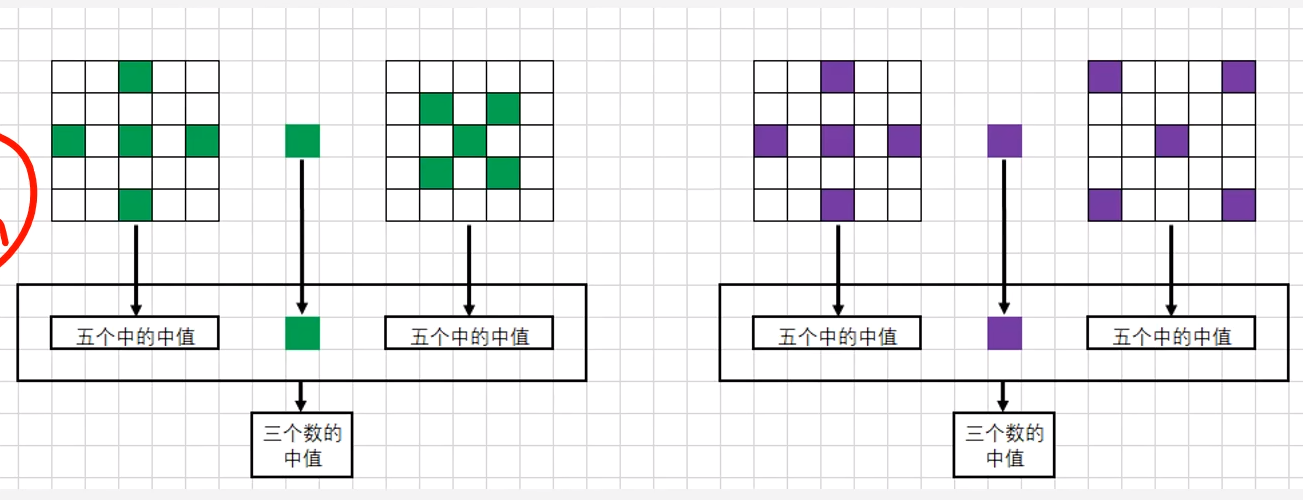
简单的中值滤波器滤波效果有限，于是就有人提出了将多个中值滤波进行多级级联实现更好的滤波效果。

如图就是一种多级级联的方式，先在窗口中定义一个'+‘和’X’形的窗口，然后分别求出这两个窗口的中位值，然后结合当前窗口的中心点就有3个候选值，再从这三个值中求出一个中位值作为滤波后的结果。

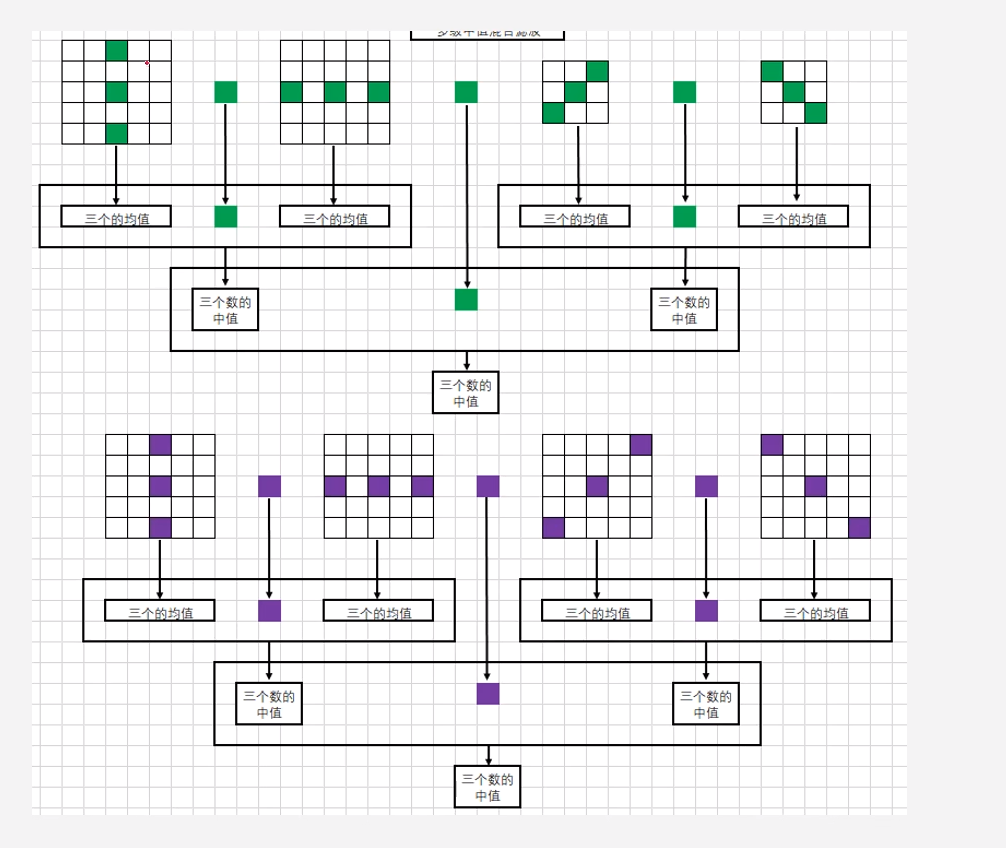
这种方式也可以直接应用到RAW图中做BNR（Bayer Noise Reduce），需要修改的就是窗口设置为5X5，然后在做滤波的时候需要区分G和RB通道，因为这个前面已经讲过，RAW图中的RGB分布是不均匀的，G占50%，R和B各占25%。

左侧就是针对G通道的滤波器，右侧是R和B通道的滤波器，都是定义了一个’+‘和’X’形的窗口，不同的只是取的点的位置不同。

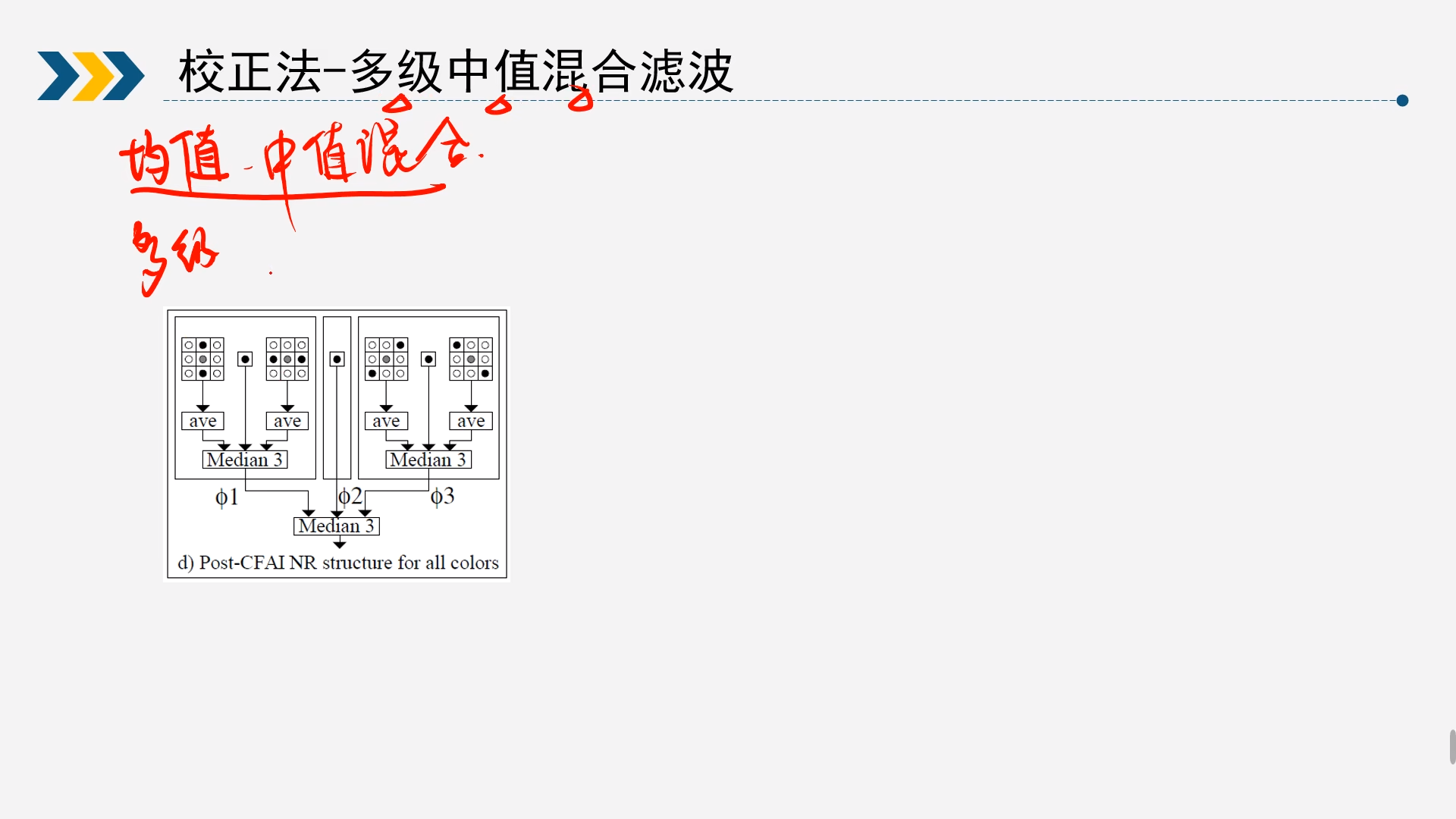
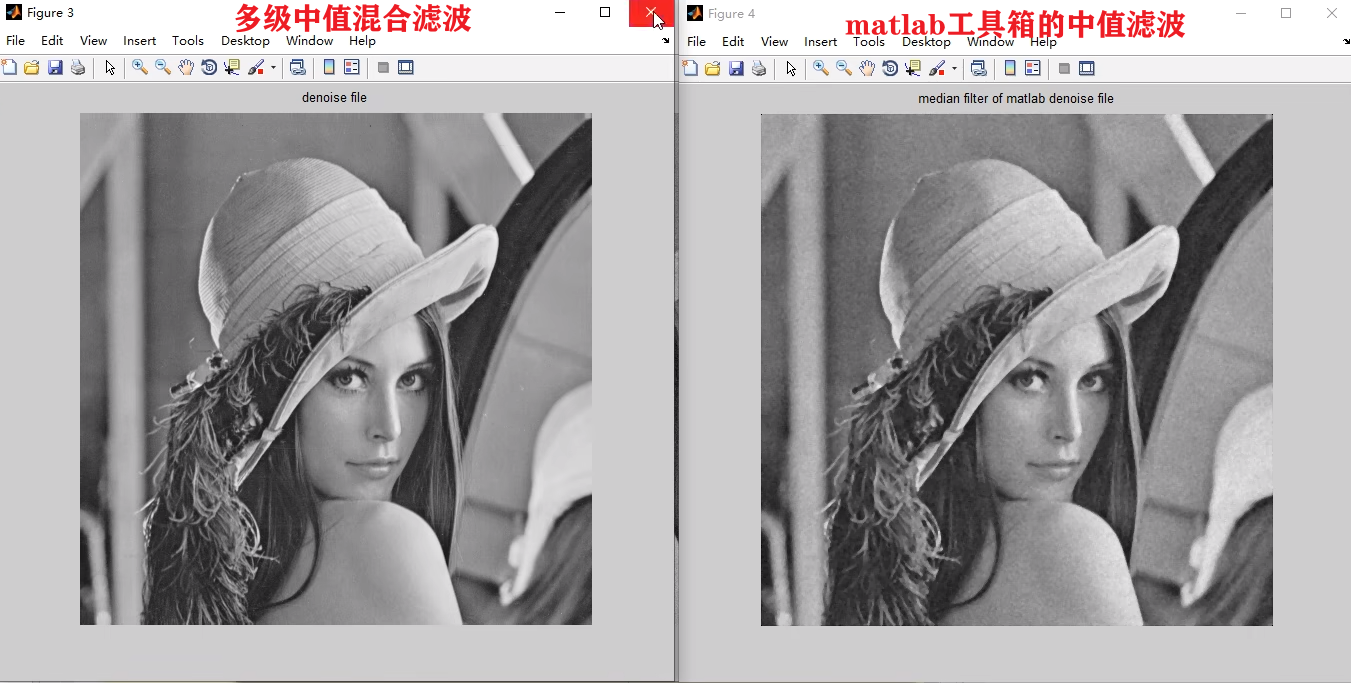
2.2.3多级中值混合滤波

前面介绍过中值滤波和均值滤波各自有各自的优点和缺点，所以就可以考虑将两者结合起来，相互弥补实现更好的滤波效果，于是就有人提出了这种多级混合滤波的方式。

算法流程：

求出竖直方向相邻三个点的均值和水平方向相邻三个点的均值，再结合当前点，用这三个点再求一个中位值；
求出45°和135°方向上的均值，然后结合当前点求出一个中位值；
两个中位值结合当前点组成新的数组，最后求一个中位值作为当前点的值完成滤波。

这样就巧妙的将均值滤波和中位值滤波结合了。然后如果应用在RAW图上，只需要对滤波器稍作改善即可。

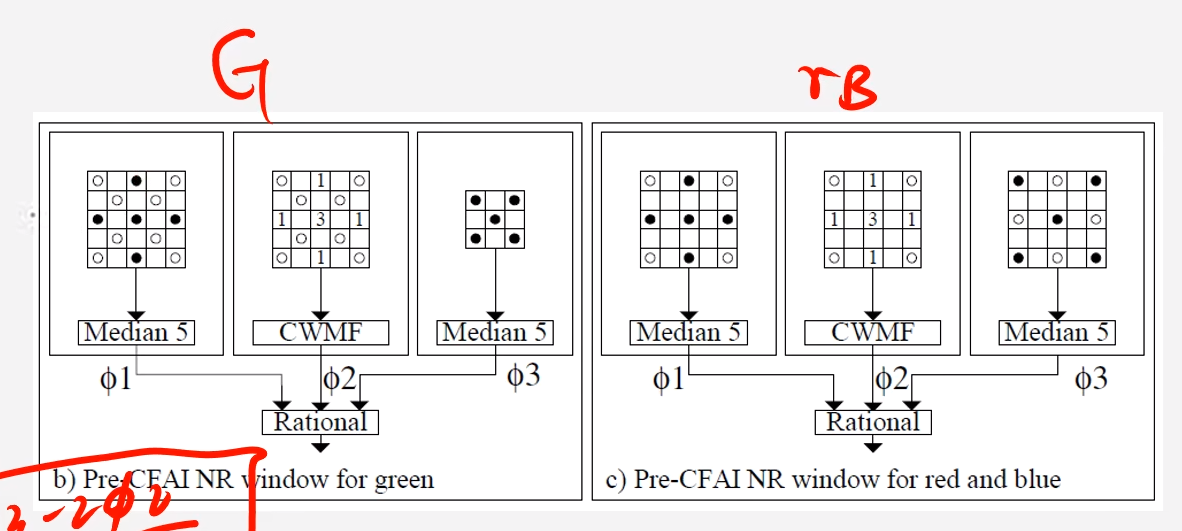
2.2.4多级中值有理混合滤波

加权中值滤波也很好理解，和加权均值滤波差不多，就是在原始数据的基础上给每个点分别赋予一个权重，然后在加权后的数据中取出中位值作为滤波后的值。

算法流程

求出’+‘形和’X’形的窗口的中位值；
对’+‘形窗口再利用CWMF（中心加权中值滤波central weighted median filter）求出一个值，CWMF是WMF（加权中值滤波weight median filter）的一种特殊情况，就是只对中心点进行加权；
对以上求出的三个参数用一下公式计算出一个新的值作为滤波后的值 $$ Res(m, n)=\phi 2(m, n)+\frac{\phi 1(m, n)-2 * \phi 2(m, n)+\phi 3(m, n)}{h+k(\phi 1(m, n)-\phi 3(m, n))} $$

一样的，稍作改动该算法就可以用于raw格式图像

3方法实现

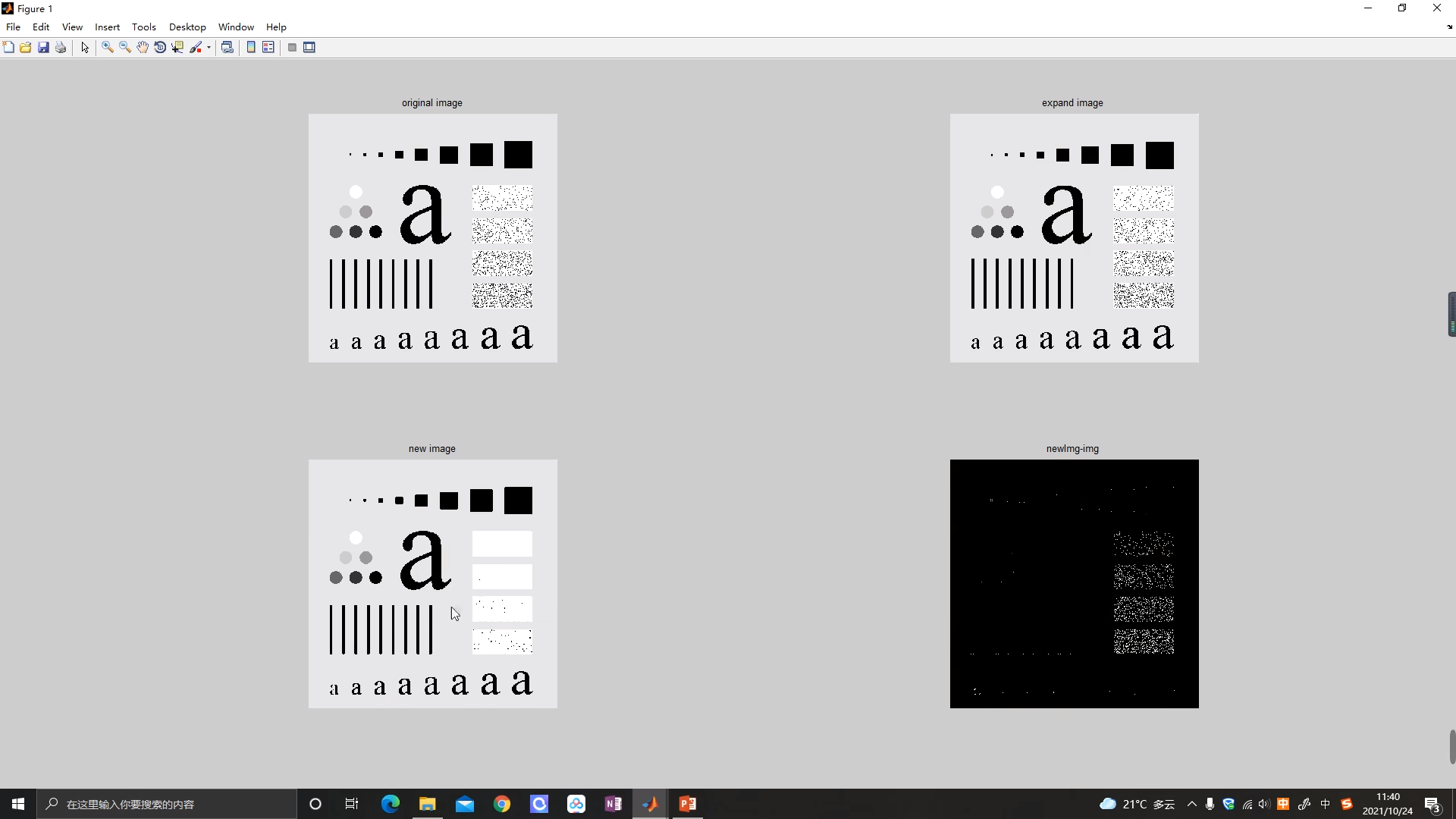
3.1均值滤波算法实现

第三幅图就是经过均值滤波处理后的效果，和第一幅图比起来变得更模糊。通过原始图像和新图像最差就能得到最后的图像，新清晰的看到边缘和部分噪点是被滤除掉了。所以这种降噪的方法有个致命的缺点就是会损失图像的边缘细节。

 1clear;
 2clc;
 3close all;
 4img = imread('./images/test_pattern_blurring_orig.tif');
 5[m, n] = size(img);
 6figure;subplot(221);imshow(img);title('original image');
 7
 8%% 运算的时候需要对边缘进行扩展
 9% 需要特殊处理四周最外圈的行和列，本算法中将其向外扩展一圈，用最外圈的值填充
10headRowMat = img(1,:);%取f的第1行
11tailRowMat = img(m,:);%取f的第m行
12% 行扩展后，列扩展时需要注意四个角需要单独扩展进去，不然就成了十字架形的
13headColumnMat = [img(1,1), img(:,1)', img(m,1)];
14tailColumnMat = [img(1,n), img(:,n)', img(m,n)];
15expandImage = [headRowMat; img; tailRowMat];
16expandImage = [headColumnMat; expandImage'; tailColumnMat];
17expandImage = uint8(expandImage');
18subplot(222);imshow(expandImage);title('expand image');
19
20% 创建新的图像
21newImg = zeros(m, n);
22% 定义模板
23meanKernal = uint8([1 1 1;
24                    1 1 1
25                    1 1 1]);
26% 遍历图像进行均值滤波
27% 1.首先提取图像中待操作的ROI
28% 2.利用模板对提取的ROI进行运算并赋值给新的图像
29for i =2: m+1
30    for j =2: n+1
31       imgRoi = [expandImage(i-1, j-1) expandImage(i-1, j) expandImage(i-1, j+1);
32                 expandImage(i  , j-1) expandImage(i  , j) expandImage(i  , j+1);
33                 expandImage(i+1, j-1) expandImage(i+1, j) expandImage(i+1, j+1)];
34       newImg(i-1, j-1) = uint8(sum(sum(imgRoi.*meanKernal))/9);
35    end
36end
37newImg = uint8(newImg);
38subplot(223);imshow(newImg);title('new image');
39subplot(224);imshow(img-newImg);title('newImg-img');

3.2双边滤波算法

 1clc;clear;close all;
 2
 3% gaussian filter
 4% the weight is only related to distance
 5x = 1:200;
 6y = 1:200;
 7[X, Y] = meshgrid(x, y);
 8D = (X-100).^2+(Y-100).^2;
 9z1 = exp(-D/2000);
10figure();
11mesh(x, y, z1)
12title('高斯模型')
13
14% add pixel value weight;
15a = ones(200)*220;
16a(:,1:100) = 20;
17a(1:100,:) = 20;
18figure();
19imshow(uint8(a));
20title('图像')
21z2 = zeros(200);
22for i=1:200
23    for j=1:200
24        z2(i, j) = exp(-(a(i, j)-220)^2/1800);
25    end
26end
27figure();
28mesh(x, y, z2);
29title('像素权重');
30z = z1.*z2;
31figure();
32mesh(x, y, z)
33title('双边模型')

高斯滤波的图形，根据像素差异通过高斯分布也很容易得到一个分布图像

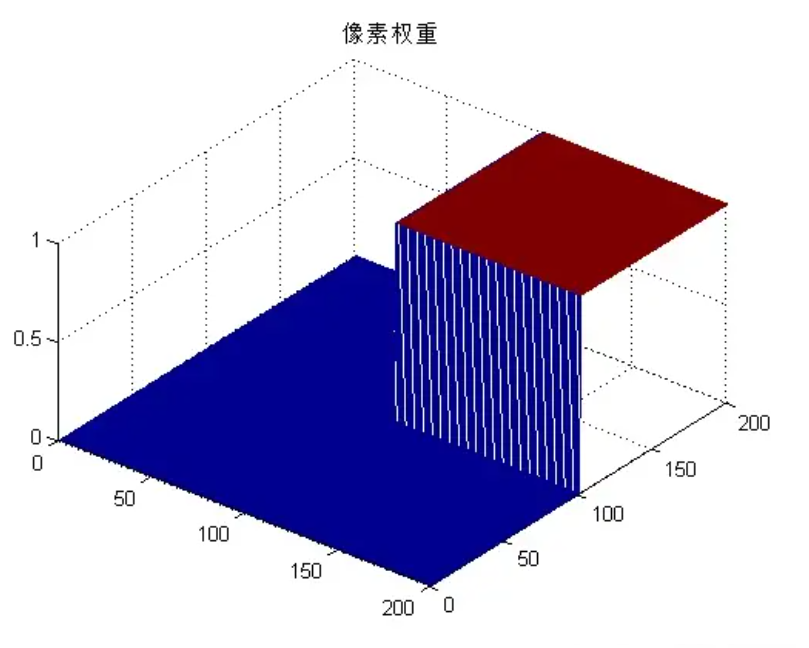
图像中同侧像素是一样的，那么相当于权重都是1，另一侧相差接近最大位数控制，权重就很小接近0，所以才边缘的时候权重就会有一个阶跃的效果，然后把这两个权重相结合就可以得到一完整的滤波器。只对同一侧的像素进行一个高斯滤波，而另一侧则保留为原来的值，这样就能起到很好的保边效果。

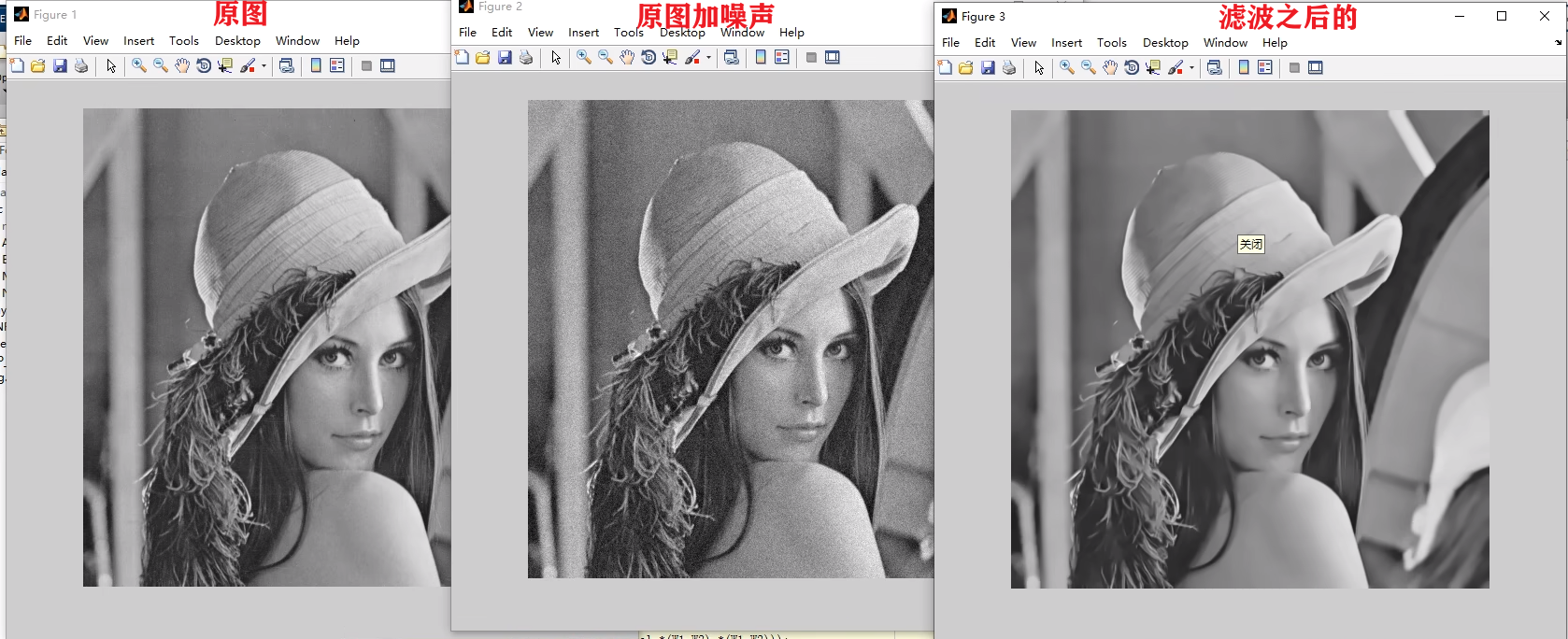
3.3NLM(非局部均值)算法

滤波之后会把噪点去除，但是帽子上的细节和头发细节会丢失

 1close all;
 2clear all;
 3clc
 4img = imread('./images/lena.bmp');
 5I = double(img);
 6% I = double(imresize(img, [64, 64]));
 7figure();
 8imshow(uint8(I));
 9I_noise = I + 10 * randn(size(I));
10figure();
11imshow(uint8(I_noise));
12
13% -----------------------------------
14ds = 2;
15Ds = 5;
16h = 10;
17% -----------------------------------
18
19[m,n] = size(I_noise);
20DenoisedImg = zeros(m,n);
21PaddedImg = padarray(I,[ds+Ds,ds+Ds],'symmetric','both');
22
23kernel = ones(2*ds+1,2*ds+1);
24kernel = kernel./((2*ds+1)*(2*ds+1));
25h2=h*h;
26
27tic
28for i=1:m
29    for j=1:n
30        num = 0;
31        i1=i+ds+Ds;
32        j1=j+ds+Ds;
33        W1=PaddedImg(i1-ds:i1+ds,j1-ds:j1+ds);  % current window
34        fprintf('=======current point: (%d, %d)\n', i, j);
35        wmax=0;
36        average=0;
37        sweight=0;
38        
39        % search window
40        % This window is not a fixed size, 
41        % it shrinks when it's in the corner or border
42        swmin = i1 - Ds;
43        swmax = i1 + Ds;
44        shmin = j1 - Ds;
45        shmax = j1 + Ds;
46        
47        for r = swmin: swmax
48            for s = shmin: shmax
49                if(r==i1 && s==j1)
50                    continue;
51                end
52                W2 = PaddedImg(r-ds:r+ds,s-ds:s+ds); % the window is to be compared with current window
53                num = num + 1;
54                % Use the mean directly in order to simplify the calculate
55                Dist2 = sum(sum(kernel.*(W1-W2).*(W1-W2)));	
56                w = exp(-Dist2/h2);   % the weight of the compared window
57                if(w > wmax)
58                    wmax = w;
59                end
60                sweight = sweight + w;  % sum the weight to normalize
61                average = average + w*PaddedImg(r,s);
62            end
63        end
64        fprintf('num of win: %d\n', num);
65        average = average + wmax*PaddedImg(i1,j1);
66        sweight = sweight+wmax;
67        DenoisedImg(i,j) = average/sweight;
68    end
69end
70figure();
71imshow(uint8(DenoisedImg));
72toc

3.4中值滤波算法

 1clear;
 2clc;
 3close all;
 4img = imread('./images/test_pattern_blurring_orig.tif');
 5[m, n] = size(img);
 6figure;subplot(221);imshow(img);title('original image');
 7
 8%% 运算的时候需要对边缘进行扩展
 9% 需要特殊处理四周最外圈的行和列，本算法中将其向外扩展一圈，用最外圈的值填充
10headRowMat = img(1,:);%取f的第1行
11tailRowMat = img(m,:);%取f的第m行
12% 行扩展后，列扩展时需要注意四个角需要单独扩展进去，不然就成了十字架形的
13headColumnMat = [img(1,1), img(:,1)', img(m,1)];
14tailColumnMat = [img(1,n), img(:,n)', img(m,n)];
15expandImage = [headRowMat; img; tailRowMat];
16expandImage = [headColumnMat; expandImage'; tailColumnMat];
17expandImage = uint8(expandImage');
18subplot(222);imshow(expandImage);title('expand image');
19
20newImg = zeros(m, n);
21for i =2: m+1
22    for j =2: n+1
23       imgRoi = [expandImage(i-1, j-1) expandImage(i-1, j) expandImage(i-1, j+1) ...
24                 expandImage(i  , j-1) expandImage(i  , j) expandImage(i  , j+1) ...
25                 expandImage(i+1, j-1) expandImage(i+1, j) expandImage(i+1, j+1)];
26       orderedList = sort(imgRoi);
27       sizeRoi = size(imgRoi);
28       newImg(i-1, j-1) = orderedList((sizeRoi(2)+1)/2);
29    end
30end
31newImg = uint8(newImg);
32subplot(223);imshow(newImg);title('new image');
33subplot(224);imshow(uint8(newImg-img));title('newImg-img');

从滤波效果图中可以看出去噪能力还可以，白块中的噪点去除了很多，而且边缘信息保留得也很好。

3.5多级中值滤波算法

 1close all;
 2clear all;
 3clc
 4img = imread('./images/lena.bmp');
 5I = double(img);
 6% I = double(imresize(img, [64, 64]));
 7figure();
 8imshow(uint8(I));
 9title('org file');
10%添加一些随机噪声
11I_noise = I + 10 * randn(size(I));
12figure();
13imshow(uint8(I_noise));
14title('noise file');
15[m,n] = size(I_noise);
16
17DenoisedImg = zeros(m,n);
18%matlab工具箱的padarray边缘扩充方法
19PaddedImg = padarray(I,[1, 1],'symmetric','both');
20
21tic
22for i = 1: m
23    for j = 1: n
24        roi = PaddedImg(i:i+2, j:j+2);
25        % first stage
26        median_HV = median([roi(1,2), roi(2,1), roi(2,2), roi(2,3), roi(3,2)]);
27        median_diag = median([roi(1,1), roi(1,3), roi(2,2), roi(3,1), roi(3,3)]);
28        % second stage
29        DenoisedImg(i, j) = median([median_HV, roi(2,2), median_diag]);
30    end
31end
32figure();
33imshow(uint8(DenoisedImg));
34title('denoise file');
35toc
36
37b = medfilt2(I_noise,[3,3]);
38figure();
39imshow(uint8(b));
40title('median filter of matlab denoise file');

3.6多级中值混合滤波算法

 1close all;
 2clear all;
 3clc
 4img = imread('./images/lena.bmp');
 5I = double(img);
 6figure();
 7imshow(uint8(I));
 8title('org file');
 9
10I_noise = I + 10 * randn(size(I));
11figure();
12imshow(uint8(I_noise));
13title('noise file');
14[m,n] = size(I_noise);
15
16DenoisedImg = zeros(m,n);
17PaddedImg = padarray(I,[1, 1],'symmetric','both');
18
19tic
20for i = 1: m
21    for j = 1: n
22        roi = PaddedImg(i:i+2, j:j+2);
23        % first stage: average and median
24        mean_V = mean(roi(:,2));
25        mean_H = mean(roi(2,:));
26        median_HV = median([mean_V, roi(2, 2)], mean_H);
27        
28        mean45 = mean([roi(1, 3), roi(2, 2), roi(3, 1)]);
29        mean135 = mean([roi(1, 1), roi(2, 2), roi(3, 3)]);
30        median_diag = median([mean45, roi(2, 2)], mean135);
31        
32        % second stage
33        DenoisedImg(i, j) = median([median_HV, roi(2,2), median_diag]);
34    end
35end
36figure();
37imshow(uint8(DenoisedImg));
38title('denoise file');
39toc
40
41b = medfilt2(I_noise,[3,3]);
42figure();
43imshow(uint8(b));
44title('median filter of matlab denoise file');

3.7多级中值有理混合滤波算法

 1close all;
 2clear all;
 3clc
 4img = imread('./images/lena.bmp');
 5I = double(img);
 6figure();
 7imshow(uint8(I));
 8title('org file');
 9
10I_noise = I + 10 * randn(size(I));
11figure();
12imshow(uint8(I_noise));
13title('noise file');
14[m,n] = size(I_noise);
15
16DenoisedImg = zeros(m,n);
17PaddedImg = padarray(I,[1, 1],'symmetric','both');
18% 这里的h和k是超参，可以是isp外部自己设置的
19h = 2;
20k = 0.01;
21
22tic
23for i = 1: m
24    for j = 1: n
25        roi = PaddedImg(i:i+2, j:j+2);
26        median_HV = median([roi(1,2), roi(2,1), roi(2,2), roi(2,3), roi(3,2)]);
27        median_diag = median([roi(1,1), roi(1,3), roi(2,2), roi(3,1), roi(3,3)]);
28        %CWMF = median([roi(1,2), roi(2,1), roi(2,2)*3, roi(2,3), roi(3,2)]);
29        %勘误修正
30        n = [1 1 1 1 3 1 1 1 1];
31        wRoi = repelem(roi(:)', n);
32        CWMF = median(wRoi);
33        
34        DenoisedImg(i, j) = CWMF + (median_HV + median_diag - 2 * CWMF) / (h + k * (median_HV - median_diag));
35    end
36end
37toc
38figure();
39imshow(uint8(DenoisedImg));
40title('denoise file');
41b = medfilt2(I_noise,[3,3]);
42figure();
43imshow(uint8(b));
44title('median filter of matlab denoise file');

isp算法学习-NR（Noise Reduce）

1200 Words|Read in about 6 Min|本文总阅读量次