统计素数个数。采用埃氏筛选。

统计素数个数 埃氏筛选

素数

素数的特性

只能被1和自身整除的自然数，0、1之外

示例：

1输入：100
2输出：25

思路

主要运用埃筛法操作，所有的合数都够拆分成两个数的相乘

2是素数，3是素数，那么两者相乘不为素数，且2是素数，与3+1的和相乘不为素数，且2是素数，与3+2的和相乘不为素数。以此类推，这些已经从当前数2可以直接判断出来的数之后就不需要再次比较了。

解题

需要建立一个表，用于判断每一个数对应是否是素数，默认全部都是素数

 1public static int eratosthenes(int n)
 2{
 3    boolean[] isPrime = new boolean[n];
 4    int count = 0;
 5    for(int i = 2; i < n; i++)
 6    {
 7        if(!isPrime[i])
 8        {
 9            count++;
10            for(int j = 2 * i; j < n; j += i)//j代表是合数
11            {
12                isPrime[j] = true;
13            }
14        }
15    }
16}

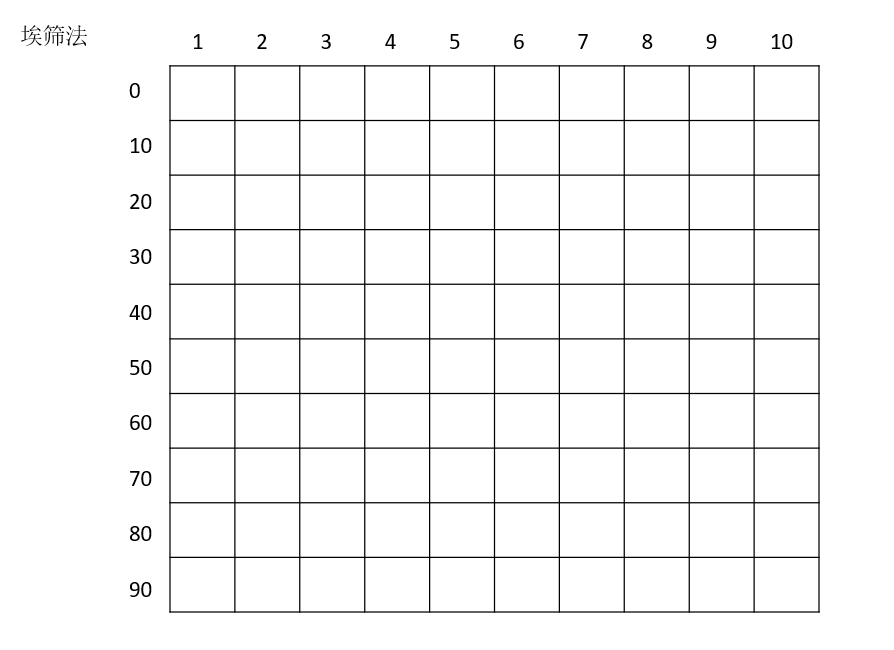
开始建表

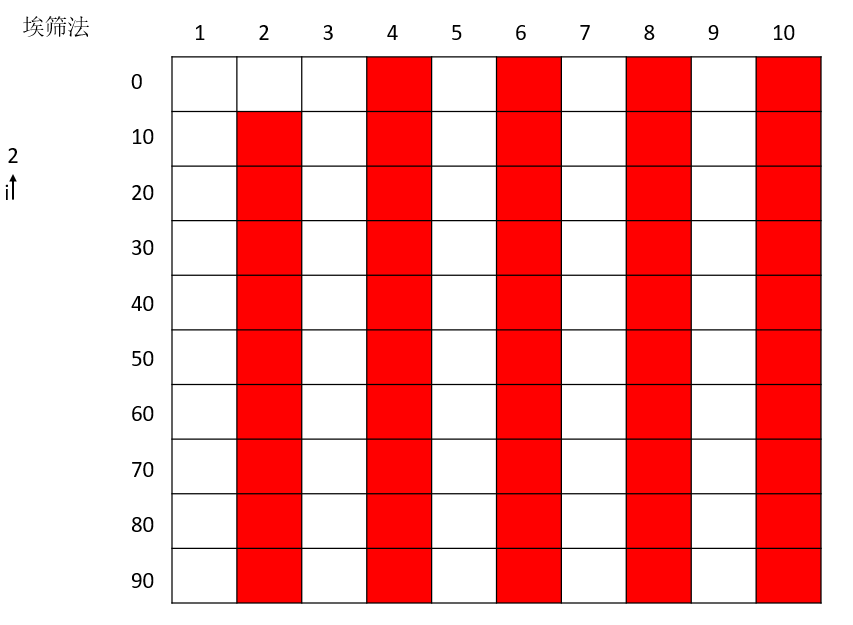
素数2的删选

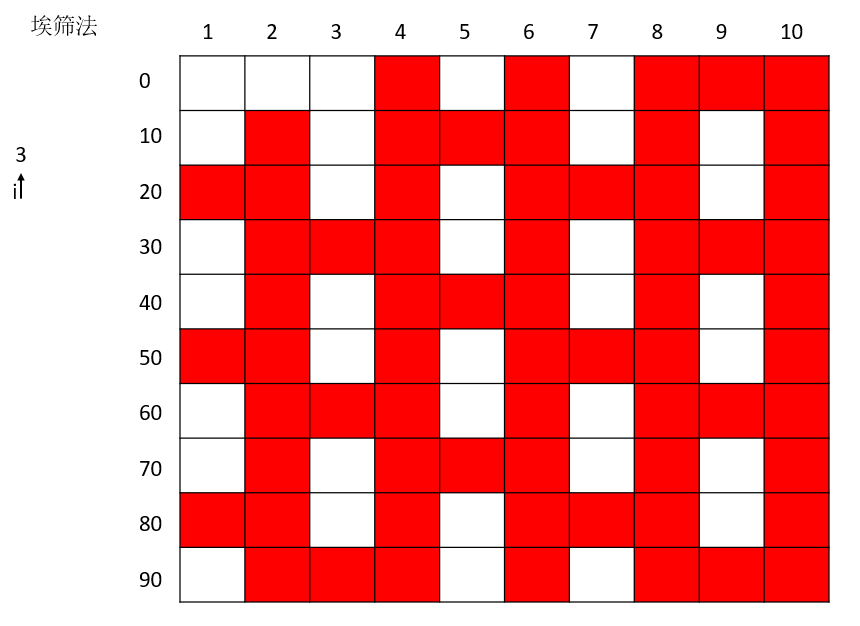
素数3的删选

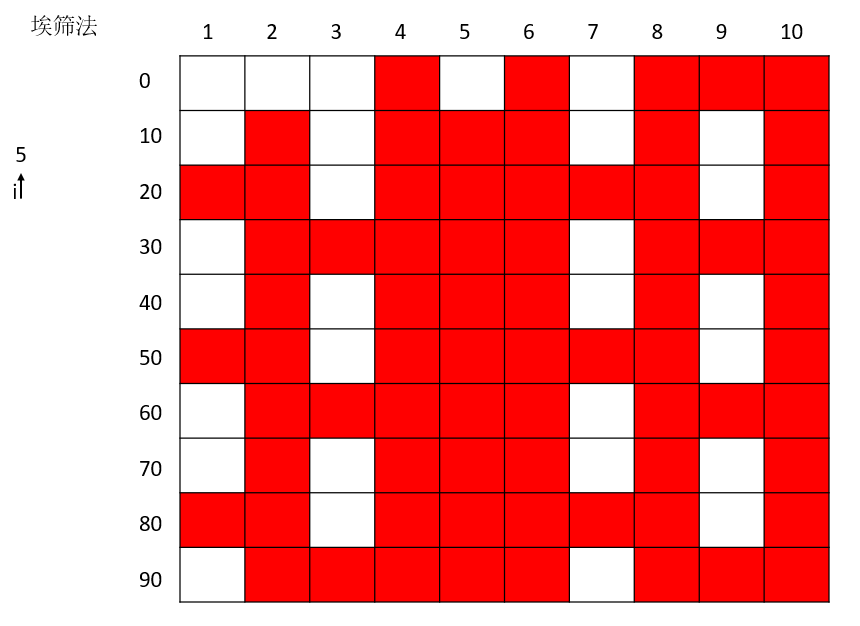
素数5的删选

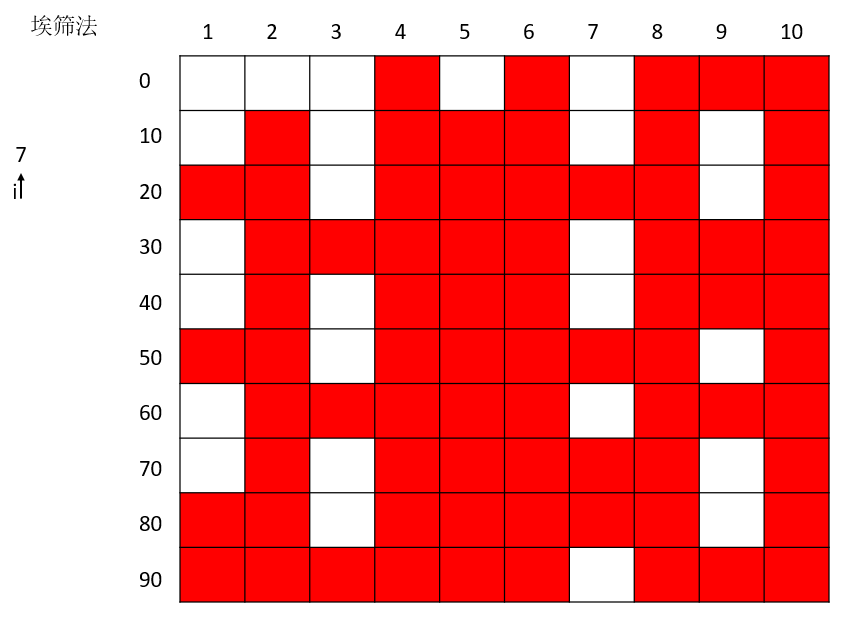
素数7的删选

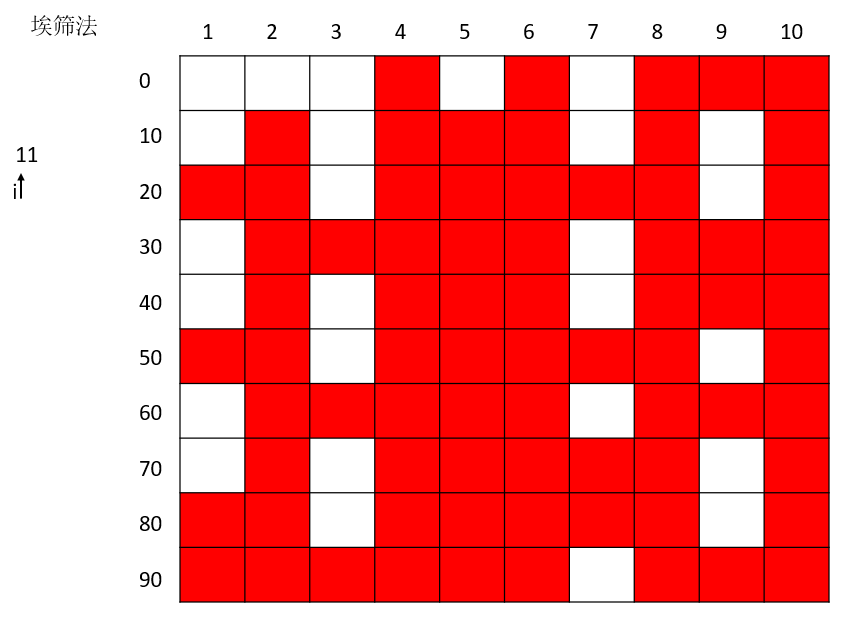
素数11的删选

发现这个时候已经和上述的素数7的删选已经一致了

将合数标记为tue, j=i*i从2*1优化而来，系数2会随着遍历递增j+=1,相当于递增了系数2)，每个合数都会有两个比本身要小的因子(0,1除外)，2*i必然会遍历到这两个因子当2递增到大于根号n时，其实后面的已经无需再判断（或者只需判断后面一段），而2到根号、实际上在i递增的过程中已经计算过了，i实际上就相当于根号。

优化埃筛法

通过上面的操作，发现其实很多步骤都有所重复，进一步优化

 1public static int eratosthenes(int n)
 2{
 3    boolean[] isPrime = new boolean[n];
 4    int count = 0;
 5    for(int i = 2; i < n; i++)
 6    {
 7        if(!isPrime[i])
 8        {
 9            count++;
10            //主要优化的是j开始的位置，从2 * j更换为j * j
11            for(int j = i * i; j < n; j += i)//j代表是合数
12            {
13                isPrime[j] = true;
14            }
15        }
16    }
17}