深度优先搜索
700 Words|Read in about 3 Min|本文总阅读量次
学习深度优先搜索(DFS)方法。
深度优先搜索
0DFS
深度优先搜索(
DFS,Depth-First Search)是搜索算法的一种,它从某一个状态开始,不断地转移状态直到无法转移,然后回退到前一步的状态,继续转移到其他状态,如此不断重复,直到找到最终的解。
1举例1
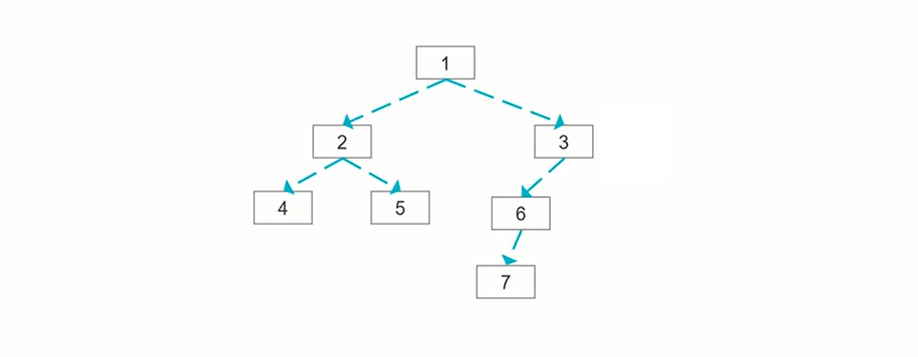
给定一个二叉树,找出其最小深度。
示例1
1输入:[1,2,4,4,5,6,7]
2输出:3
思路
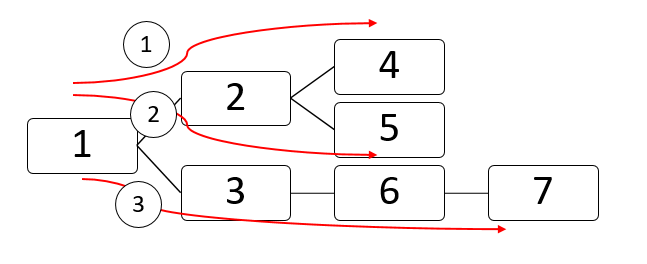
上面这个二叉树的遍历顺序,1->2->4->5->3->6->7
解题
1static class TreeNode
2{
3 int val;
4 TreeNode left;
5 TreeNode right;
6 TreeNode(int val, TreeNode left, TreeNode right)
7 {
8 this.val = val;
9 this.left = left;
10 this.right = right;
11 }
12}
13
14public static void main(String[] args)
15{
16 TreeNode ndoe7 = new TreeNode(7, null, null);
17 TreeNode ndoe6 = new TreeNode(6, node7, null);
18 TreeNode ndoe5 = new TreeNode(5, null, null);
19 TreeNode ndoe4 = new TreeNode(4, null, null);
20 TreeNode ndoe3 = new TreeNode(3, node6, null);
21 TreeNode ndoe2 = new TreeNode(2, node4, node5);
22 TreeNode ndoe1 = new TreeNode(1, node2, node3);
23 System.out.println(minDepth(node1));
24}
25
26public static int minDepth(TreeNode node)
27{
28 if(node == null)
29 {
30 return 0;
31 }
32
33 if(node.left == null && node.right == null)
34 {
35 return 1;
36 }
37 //计算出min,minDepth(node.left),minDepth(node.right)三者之间的最小值
38 int min = Integer.MAX_VALUE;
39 if(node.left != null)
40 {
41 min = Math.min(minDepth(node.left), min);
42 }
43
44 if(node.right != null)
45 {
46 min = Math.min(minDepth(node.right), min);
47 }
48 return min + 1;
49}
2举例2
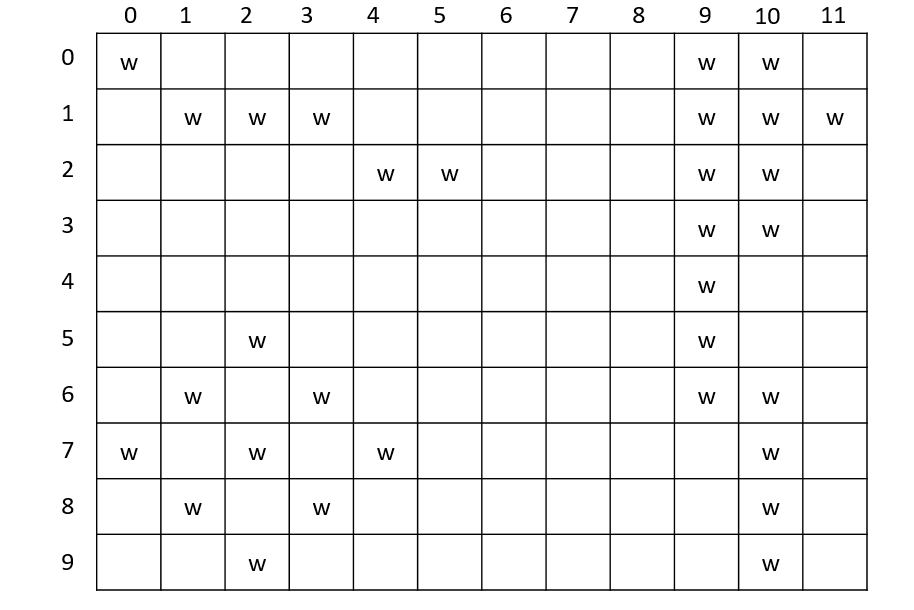
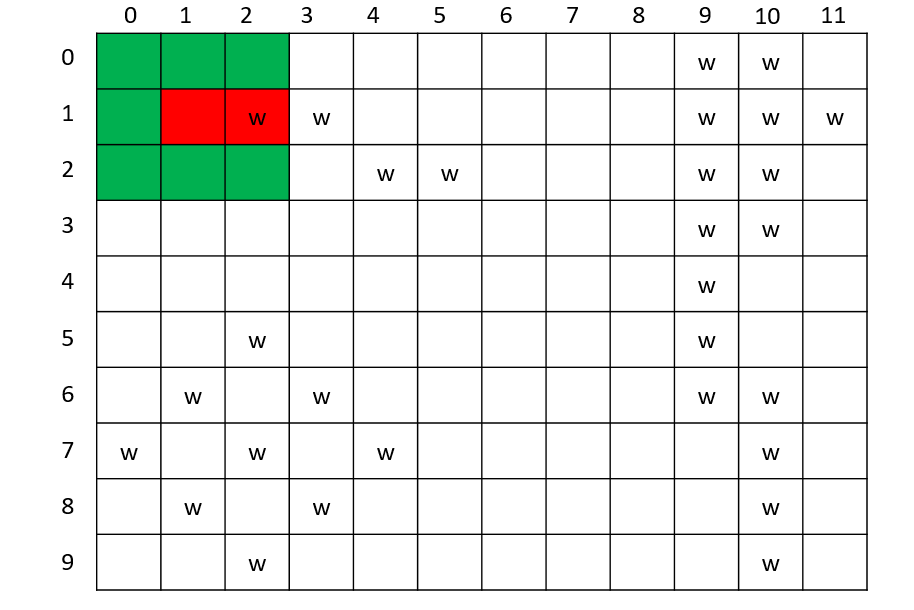
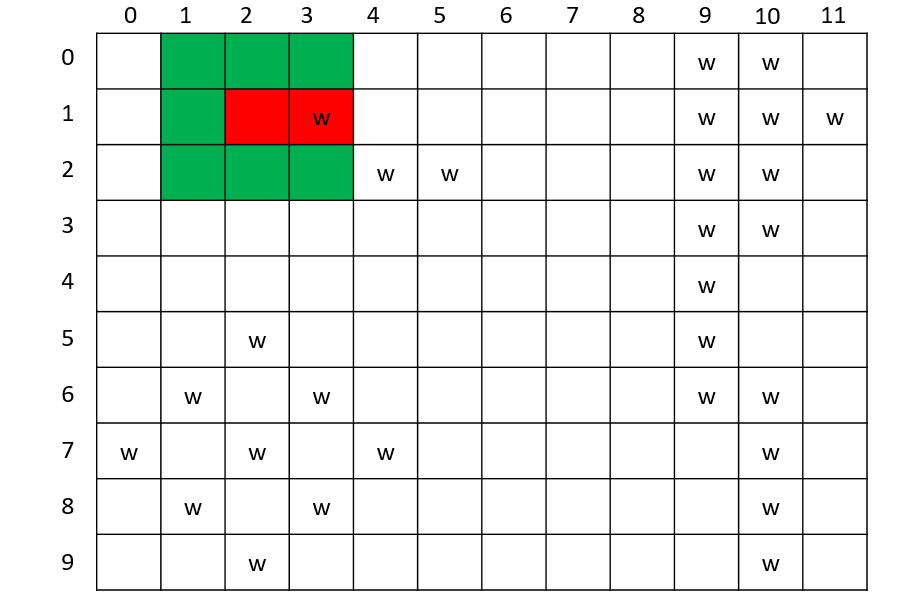
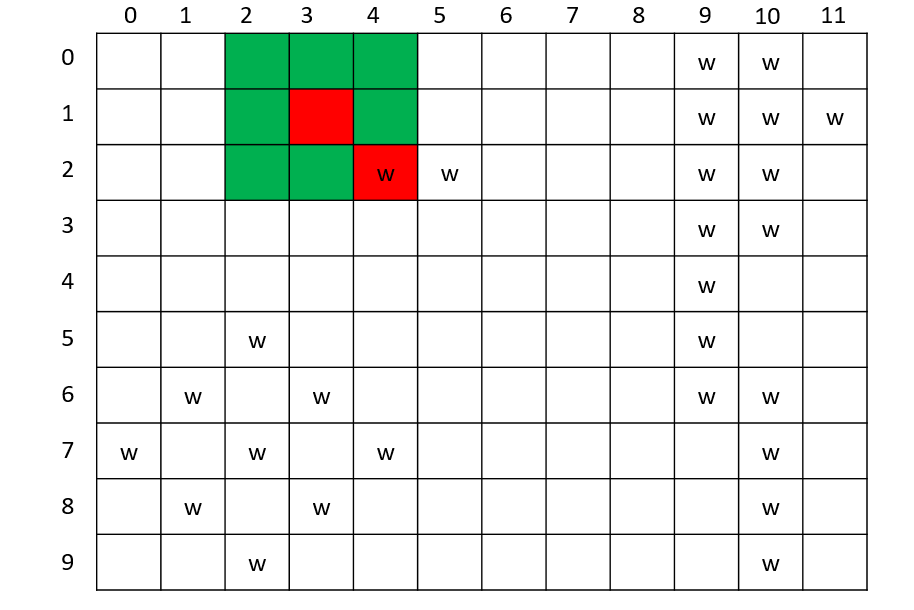
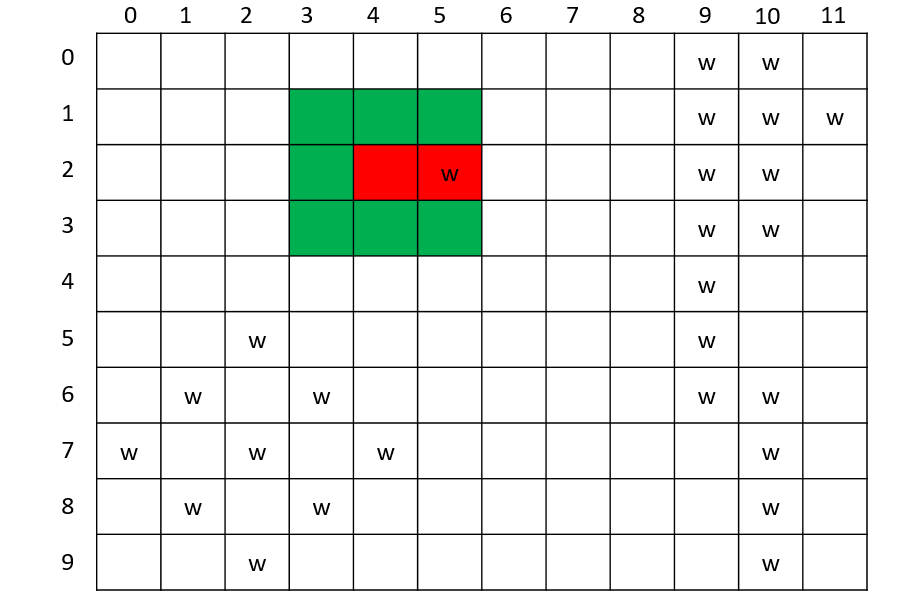
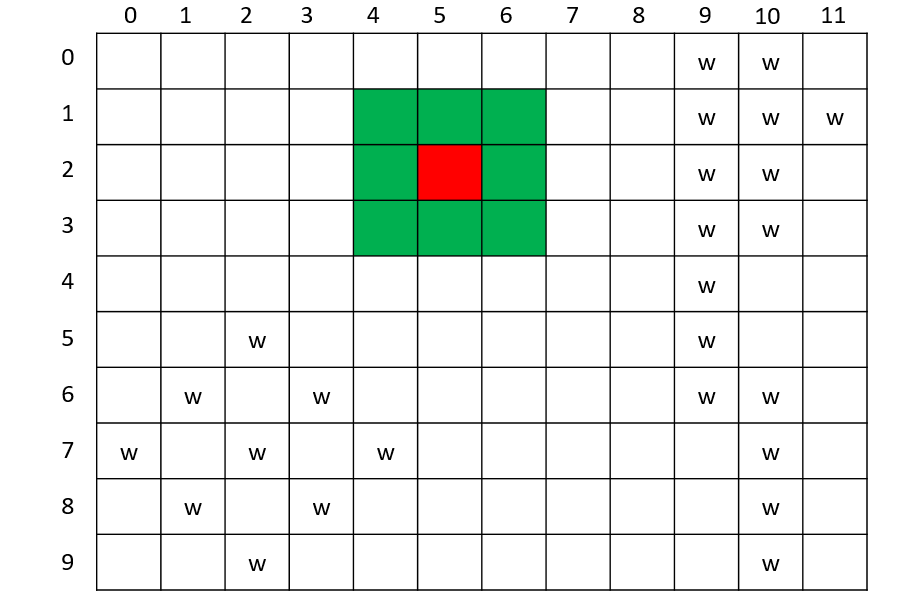
有一个大小为N × M的园子,雨后积起了水,八连通的积水被认为是连接在一起的,请求出园子里共有多少个水洼。(八连通指的是下图中相对w的*的部分)
1* * *
2* w *
3* * *
- 第一行输入一个整数
N - 第二行输入一个整数
M - 接下来的
N行M列表示园子的范围,其中“w”为积水
限制条件:
*N , M ≤ 100
示例2:
1样例输入:
2w........ww.
3.www.....www
4....ww...ww.
5.........ww.
6.........w..
7..w......w..
8.w.w.....ww.
9w.w.w.....w.
10.w.w......w.
11..w.......w.
12样例输出:
133
思路
- 可以从任意一个
w的位置入手,将这个位置用"."代替 - 搜索它所对应八连通的位置,如果搜索的位置在园子内,并且值为
w,则递归调用自身,重复上述步骤; - 直到某个点的八连通位置内没有
w时退出循环
依次对园子内的每个点进行如上操作,则DFS被调用的次数即为水洼的个数。
解题
1#include <bits/stdc++.h>
2using namespace std;
3#define max_N 101
4int N,M;
5char field[max_N][max_N];//园子
6void dfs (int x, int y) {
7 //将该位置用"."替换
8 field[x][y] = '.';
9
10 //循环遍历八连通的各个点
11 for (int dx = -1; dx <= 1; dx++) {
12 for (int dy = -1; dy <= 1; dy++) {
13 int nx = x + dx, ny = y + dy;
14 //判断该点是否在园子内并且是否为积水
15 if (nx >= 0 && nx <= N && ny >= 0 && ny <= M && field[nx][ny] == 'w') {
16 dfs(nx, ny);
17 }
18 }
19 }
20 return ;
21}
22void solve () {
23 int res = 0;
24 for (int i = 0; i < N; i++) {
25 for (int j = 0; j < M; j++) {
26 if (field[i][j] == 'w') {
27 dfs(i, j);
28 res++;
29 }
30 }
31 }
32 cout << res;
33}
34int main () {
35 cin >> N >> M;
36 for (int i = 0; i < N; i++) {
37 for (int j = 0; j < M; j++) {
38 cin >> field[i][j];
39 }
40 }
41 solve();
42 return 0;
43}
原始数据
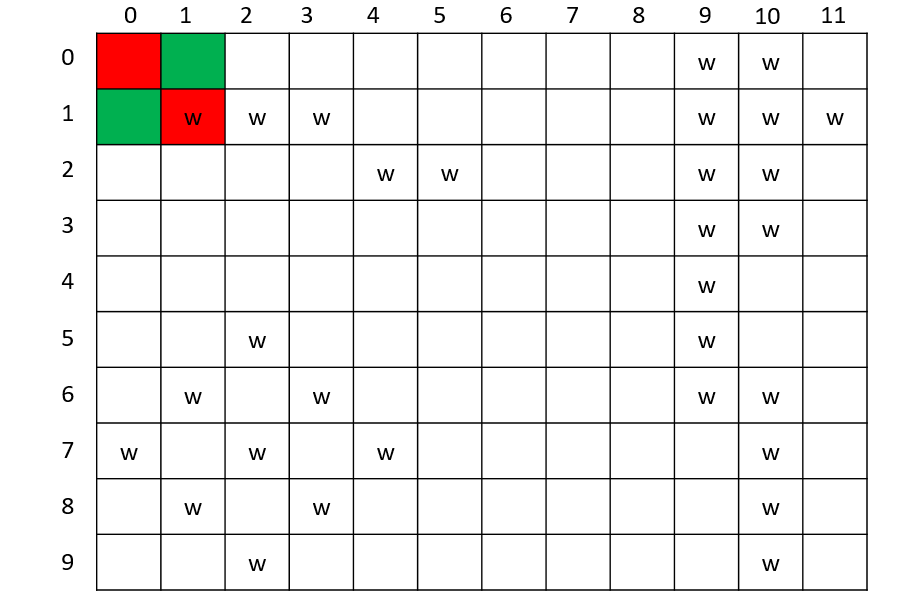
第一次遍历
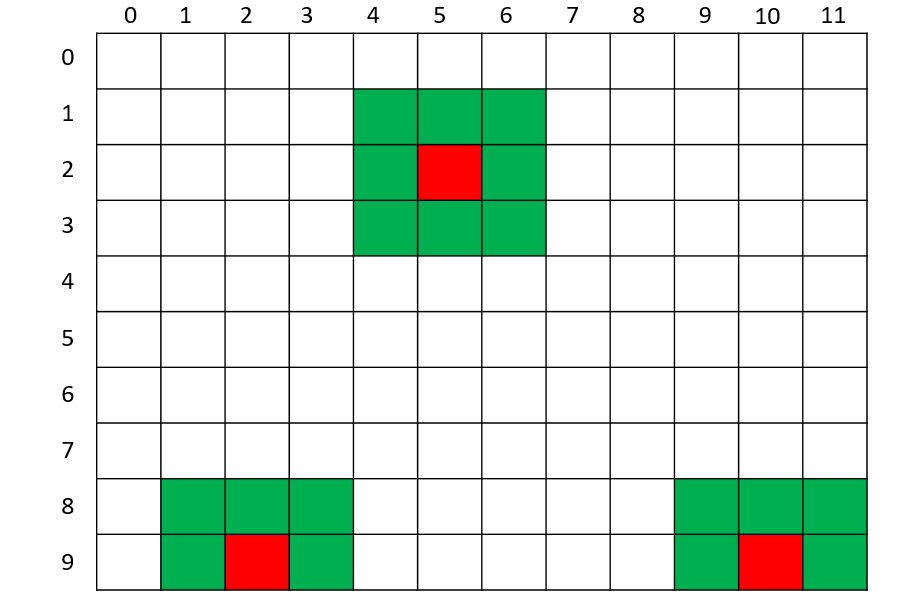
第二次遍历
第三次遍历
第四次遍历
第五次遍历
第六次遍历
最终遍历完成
遍历完成,得到3处水洼
3深度优先搜索算法框架
1void DFS(当前节点){
2 对当前节点的访问;`在这里插入代码片`
3 标记当前节点为已访问;
4 for(下一节点 : 当前节点的邻接列表){
5 剪枝(如果下一节点已经访问过就跳过);
6 DFS(下一节点);
7 }
8}
二叉树的前中后序遍历也可以是深度优先搜索
二叉树的前序遍历
当前结点->当前的左孩子结点->当前的右孩子结点
1//二叉树前序DFS搜索
2void DFS(TreeNode* root){
3 if(root == nullptr) return;
4 cout << root->val << " "; //输出当前节点
5 //这里不需要标记当前节点为已访问,因为二叉树不会往回走
6 DFS(root->lchild);
7 DFS(root->rchild);
8}
二叉树的中序遍历
当前的左孩子结点->当前结点->当前的右孩子结点
1//二叉树中序DFS搜索
2void DFS(TreeNode* root){
3 if(root == nullptr) return;
4 DFS(root->lchild);
5 cout << root->val << " "; //输出当前节点
6 DFS(root->rchild);
7}
二叉树的后序遍历
当前的左孩子结点->当前的右孩子结点->当前结点
1//二叉树后序DFS搜索
2void DFS(TreeNode* root){
3 if(root == nullptr) return;
4 DFS(root->lchild);
5 DFS(root->rchild);
6 cout << root->val << " "; //输出当前节点
7}
二维矩阵深度优先搜索模板
1int m = matrix.size(); //行数
2int n = matrix[0].size(); //列数
3vector<vector<int>> visited(m, vector<int>(n, 0)); //用来标记已经访问过的节点
4int directions[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; //行进方向
5
6
7void DFS(vector<vector<int>> &matrix, int x, int y){
8 if(matrix[x][y] == target)
9 return;
10 visited[x][y] = 1; //标记当前节点为已访问
11
12 for(int i = 0; i < 4; i++){
13 int new_x = x + directions[i][0];
14 int new_y = y + directions[i][1];
15 //这里一定要把visites[new_x][new_y]放在最后,因为计算后的new_x和new_y值有可能已经超过visited的下标访问范围
16 if(new_x < 0 || new_x >= m || new_y < 0 || new_y >= n || visited[new_x][new_y]) continue;
17 DFS(matrix, new_x, new_y);
18 }
19}