求斐波那契数列第N位的值。采用双指针迭代方法。

斐波那契数列

每一位的值等于他前两位数字之和。前两位固定0,1,1,2,3,5,8…

求斐波那契数列第N位的值

求解斐波那契数组

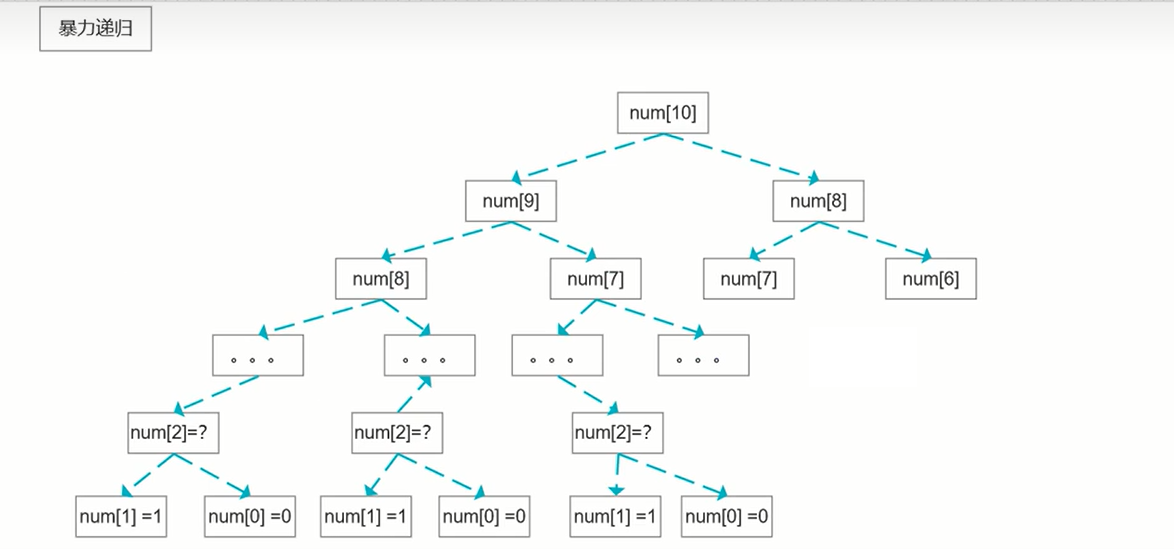
1暴力递归

时间复杂度o(n^2^)

 1public static int calculate(int num)
 2{
 3    if(0 == num)
 4    {
 5        return 0;
 6    }
 7    
 8    if(1 == num)
 9    {
10        return 1;
11    }
12    
13    return calculate(num - 1) + calculate(num - 2);
14}

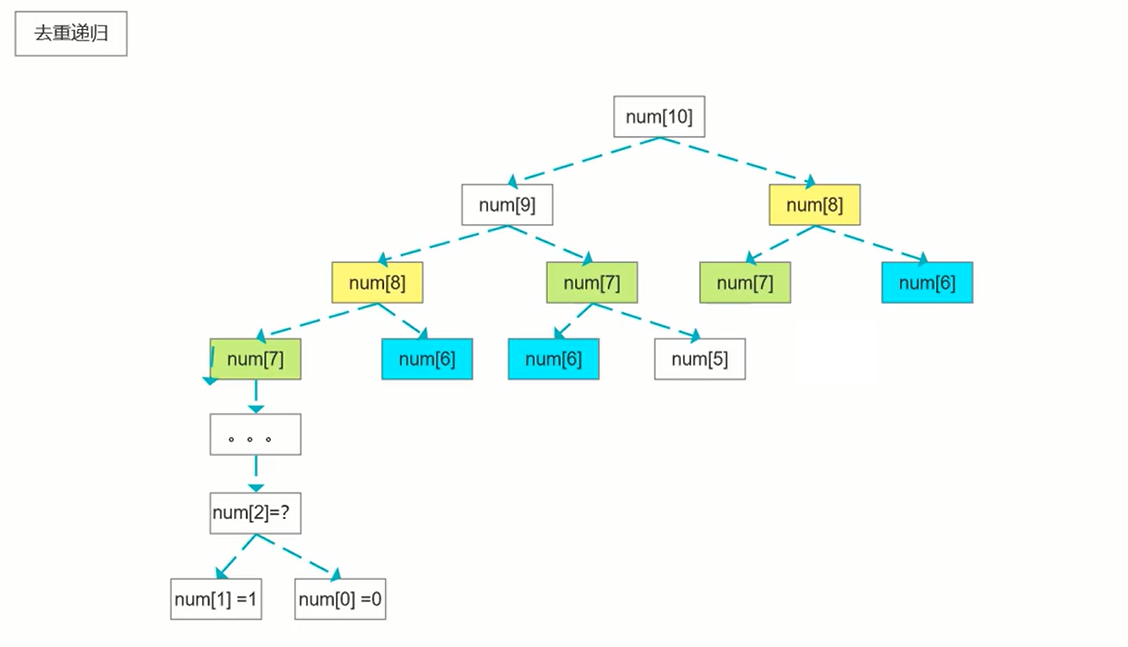
2去重递归

因为虽然上面直接递归操作可以满足，但是出现了很多重复计算的步骤.

时间复杂度o(n)，空间复杂度o(n)

 1//通过数组的形式
 2public static int calculate(int num)
 3{
 4    int[] arr = new int[num + 1];
 5    return recurse(arr, num);
 6}
 7
 8private static int recurse(int[] arr, int num)
 9{
10    if(0 == num)
11    {
12        return 0;
13    }
14    
15    if(1 == num)
16    {
17        return 1;
18    }
19    
20    if(arr[num] != 0)
21    {
22        return arr[num];
23    }
24    arr[num] = recurse(arr, num - 1) + recurse(arr, num - 2);
25    return arr[num];
26}

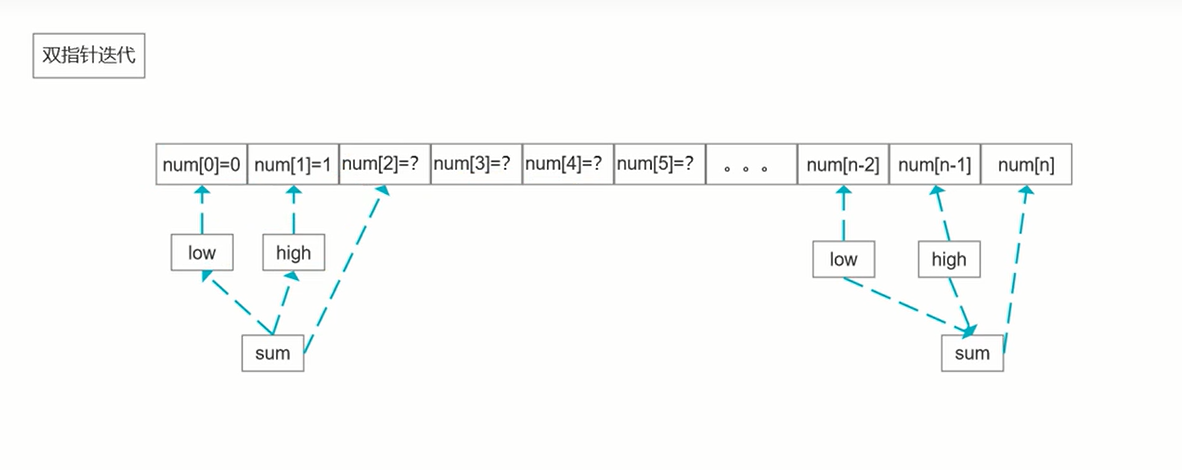
双指针迭代

进一步优化，其实只需要两个变量（双指针）就可以

时间复杂度o(n)，空间复杂度o(1)

 1//双指针迭代
 2public static int calculate(int num)
 3{
 4    if(0 == num)
 5    {
 6        return 0;
 7    }
 8    
 9    if(1 == num)
10    {
11        return 1;
12    }
13    
14    int low = 0;
15    int high = 1;
16    for(int i = 2; i < num; i++)
17    {
18        int sum = low + high;
19        low = high;
20        high = sum;
21    }
22    
23    return high;
24}