广度优先搜索
700 Words|Read in about 4 Min|本文总阅读量次
学习广度优先搜索(BFS)方法。
广度优先搜索
0BFS
宽度优先搜索(BFS,Breath-First Search)又称广度优先搜索,也是搜索算法的一种,它与深度优先搜索类似,从某个状态出发,搜索所有可到达的状态。
广度优先搜索与深度优先搜索相反,广度优先自上而下,按层序遍历来,直到出现第一个叶子结点满足条件并且退出。
1举例1
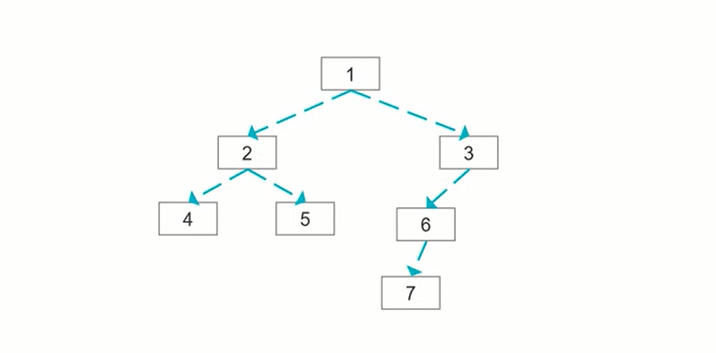
给定一个二叉树,找出其最小深度。
示例1
1输入:[1,2,4,4,5,6,7]
2输出:3
思路
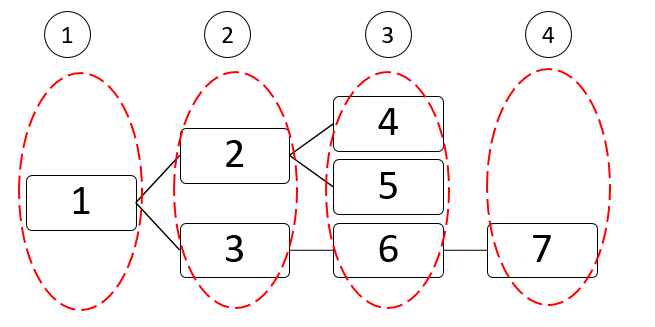
上面这个二叉树的遍历顺序,1->2->3->4->5->6->7
解题
1static class TreeNode
2{
3 int val;
4 TreeNode left;
5 TreeNode right;
6 int deep;
7 TreeNode(int val, TreeNode left, TreeNode right)
8 {
9 this.val = val;
10 this.left = left;
11 this.right = right;
12 }
13}
14
15public static void main(String[] args)
16{
17 TreeNode ndoe7 = new TreeNode(7, null, null);
18 TreeNode ndoe6 = new TreeNode(6, node7, null);
19 TreeNode ndoe5 = new TreeNode(5, null, null);
20 TreeNode ndoe4 = new TreeNode(4, null, null);
21 TreeNode ndoe3 = new TreeNode(3, node6, null);
22 TreeNode ndoe2 = new TreeNode(2, node4, node5);
23 TreeNode ndoe1 = new TreeNode(1, node2, node3);
24 System.out.println(minDepth(node1));
25}
26
27public static int minDepth(TreeNode root)
28{
29 if(node == null)
30 {
31 return 0;
32 }
33 //为了保证层序遍历,需要先进先出,这里使用队列
34 Queue<TreeNode> queue = new LinkedList<TreeNode>();
35 //根节点深度为1
36 root.deep = 1;
37 queue.offer(root);
38 while(!queue.isEmpty())
39 {
40 TreeNode node = queue.poll();
41 if(node.left == null && node.right == null)
42 {
43 return node.deep;
44 }
45
46 if(node.left != null)
47 {
48 node.left.deep = node.deep + 1;
49 queue.offer(node.left);
50 }
51
52 if(node.right != null)
53 {
54 node.right.deep = node.deep + 1;
55 queue.offer(node.right);
56 }
57 }
58 return 0;
59}
2举例2
迷宫的最短路径
给定一个大小为N × M的迷宫。迷宫由通道和墙壁组成,每一步可以向邻接的上下左右四格的通道移动。请求出从起点到终点所需的最小步数。请注意,本题假定从起点一定可以移动到终点。
- 第一行输入一个整数
N - 第二行输入一个整数
M - 接下来的
N行M列为迷宫矩阵,“#”表示墙壁,“.”表示通道,“S”表示起点,“G”表示终点
限制条件:
N , M ≤ 100
示例2
1样例输入:
210
310
4#S######.#
5......#..#
6.#.##.##.#
7.#........
8##.##.####
9....#....#
10.#######.#
11....#.....
12.####.###.
13....#...G#
14样例输出:
1522
思路
宽度优先搜索按照距开始状态由近及远的顺序进行搜索,因此可以很容易地用来求最短路径、最少操作之类的问题的答案。
- 转移的方式为四方向移动,状态数与迷宫的大小是相等的,所以复杂度为
O ( 4 × N × M )=O ( N × M ) - 只要将已经访问过的状态用标记管理起来,就可以很好地做到由近及远的搜索,这个问题要求最短距离,不妨用数组
d[N][N]来把最短距离保存起来初始时用一个充分大的常数INF来进行初始化 - 虽然到达终点时会停止搜索,可如果继续下去直到队列为空的话,就可以计算出各个位置的最短距离。
解题
1#include <bits/stdc++.h>
2using namespace std;
3#define max_N 20
4const int INF = 100000000;
5
6char maze[max_N][max_N + 1];
7int N, M;
8int sx, sy; //起点
9int px, py; //终点
10int d[max_N][max_N];
11
12//4个方向移动的分量
13int dx[4] = {1, 0, -1, 0};
14int dy[4] = {0, 1, 0, -1};
15
16//使用pair表示状态时,使用typedef会更加方便一些
17typedef pair<int, int> P;
18
19int bfs () {
20 queue<P> que;
21 //初始化
22 for (int i = 0; i < N; i++) {
23 for (int j = 0; j < M; j++) {
24 d[i][j] = INF;
25 if (maze[i][j] == 'S') {
26 sx = i;
27 sy = j;
28 }
29 if (maze[i][j] == 'G') {
30 px = i;
31 py = j;
32 }
33 }
34 }
35
36 //起点加入队列
37 que.push(P(sx, sy));
38 d[sx][sy] = 0;
39
40 //不断循环直到队列长度为0
41 while (que.size()) {
42 //从队列中取出第一个元素
43 P p = que.front();
44 que.pop();
45
46 //如果这个点是终点,则结束搜索
47 if (p.first == px && p.second == py) {
48 break;
49 }
50
51 //四个方向的循环
52 for (int i = 0; i < 4; i++) {
53 int nx = p.first + dx[i];
54 int ny = p.second + dy[i];
55
56 //判断是否可以移动,以及是否已经被放问过
57 if (nx > 0 && nx < N && ny > 0 && ny < M && maze[nx][ny] != '#' && d[nx][ny] == INF) {
58 //如果可以移动,则讲该点加入到队列,并将起点到该点的距离确定为到p的距离+1
59 que.push(P(nx, ny));
60 d[nx][ny] = d[p.first][p.second] + 1;
61 }
62 }
63 }
64 return d[px][py];
65}
66
67int main () {
68 cin >> N >> M;
69 for (int i = 0; i < N; i++) {
70 for (int j = 0; j < M; j++) {
71 cin >> maze[i][j];
72 }
73 }
74 int res = bfs();
75 cout << res;
76 return 0;
77}
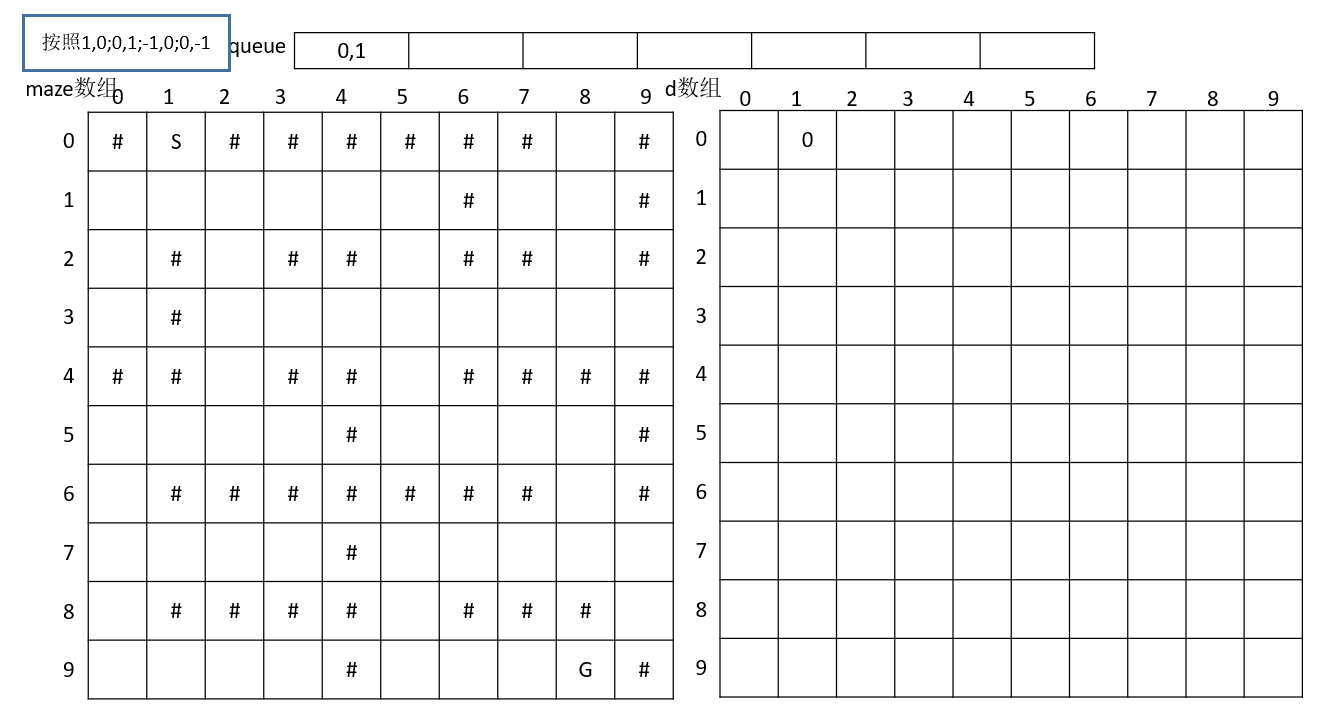
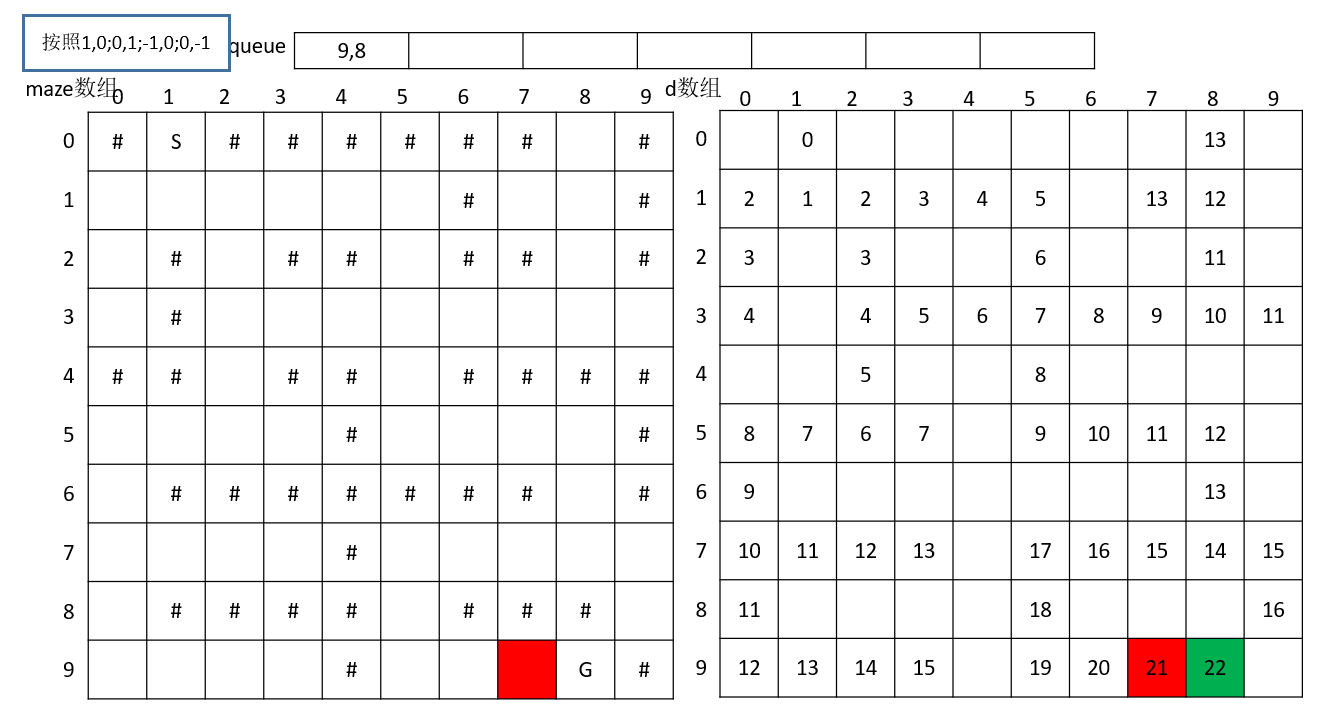
准备开始的时候,找到起始点S
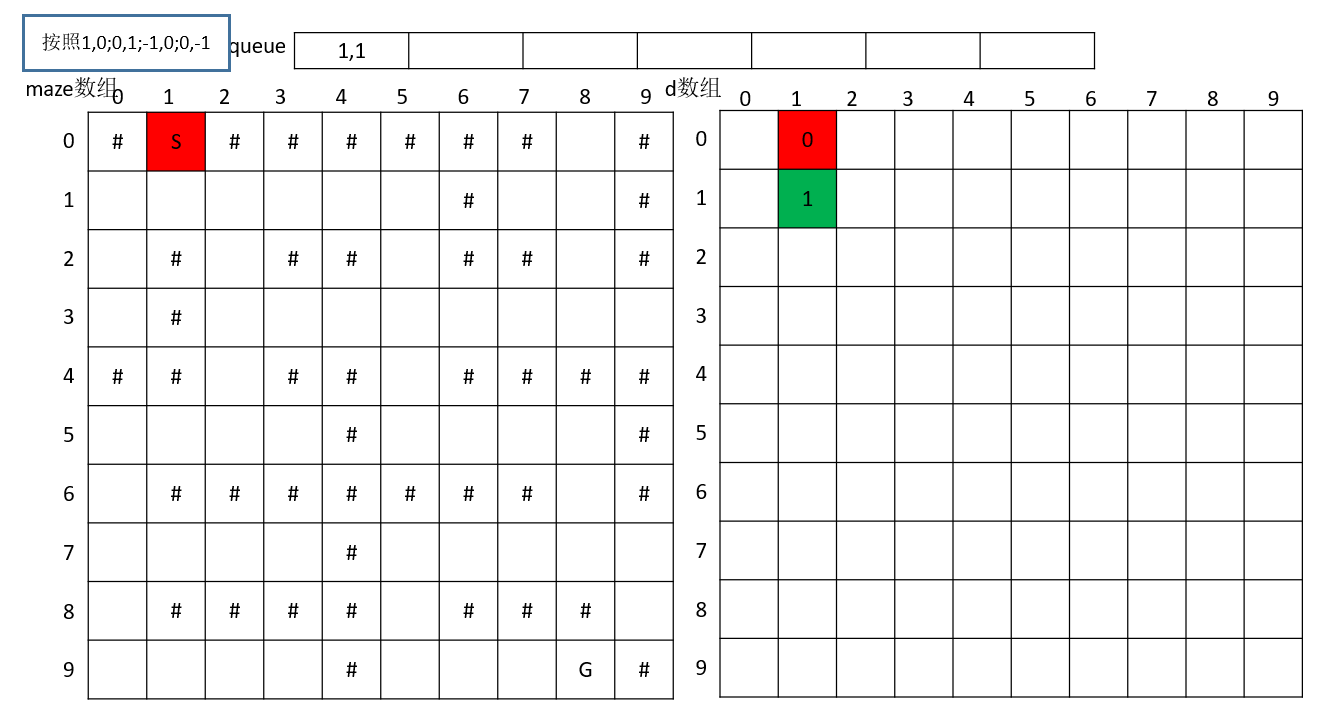
逆时针搜索下一个点,搜到(1,1)
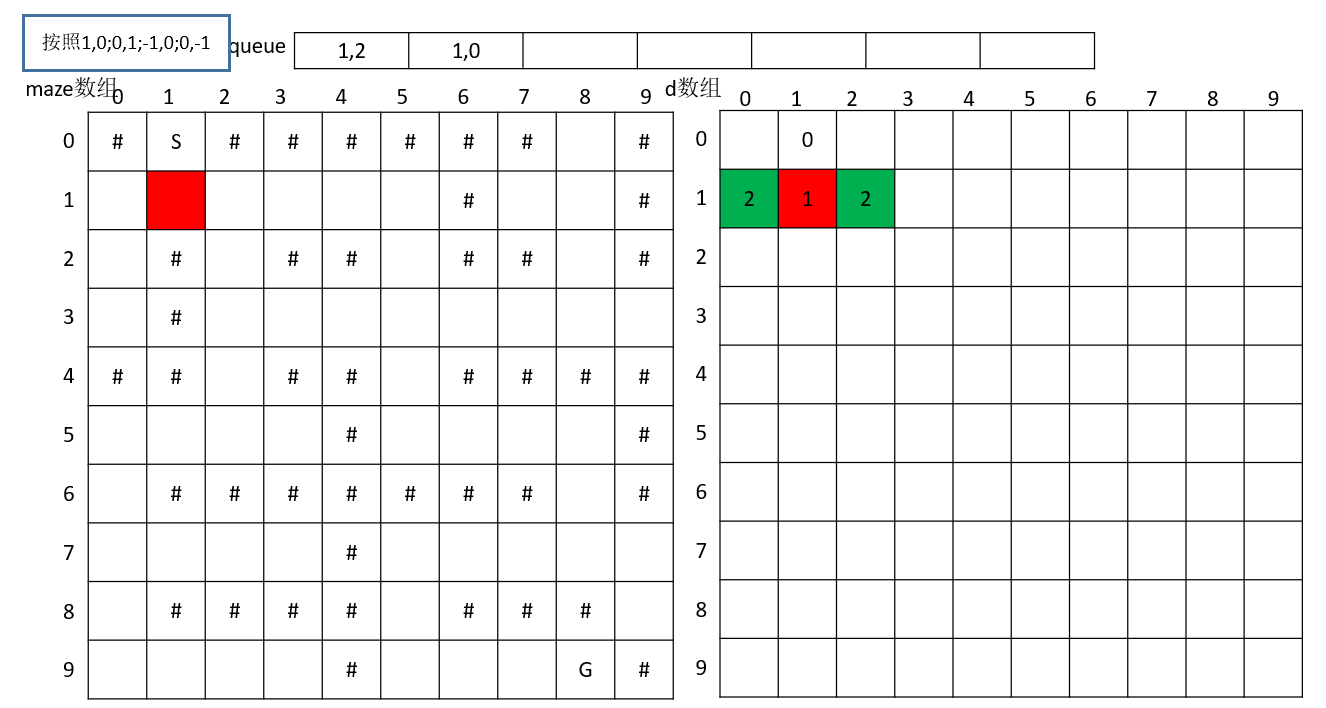
逆时针搜索下一个点,搜到(1,2),(1,0)
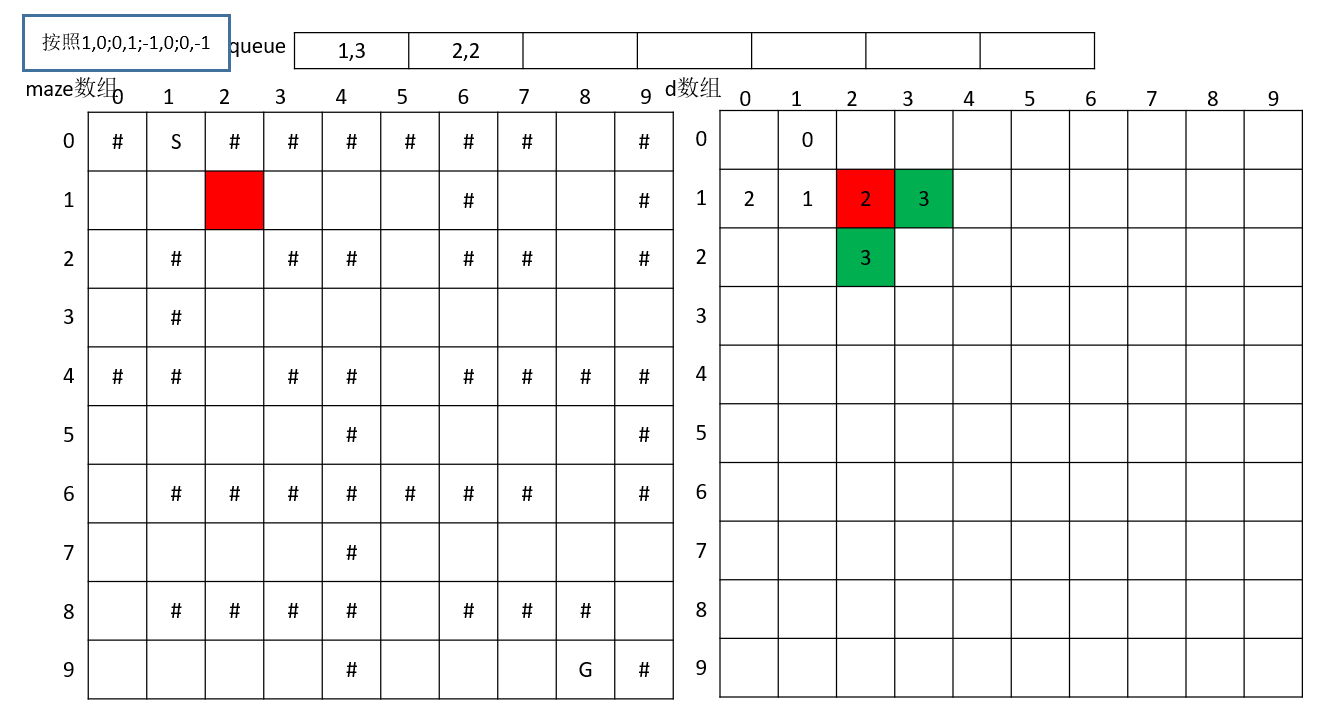
逆时针搜索下一个点,搜到(1,3),(2,2)
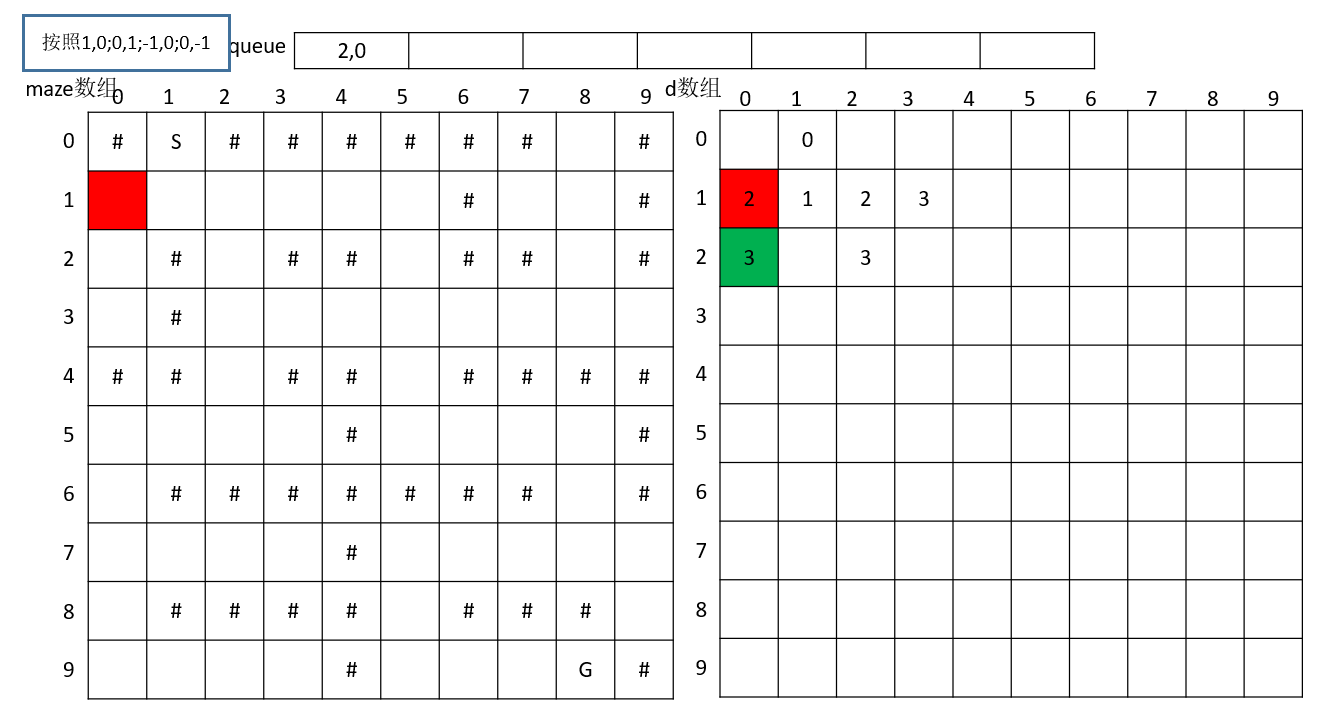
逆时针搜索下一个点,搜到(2,0)
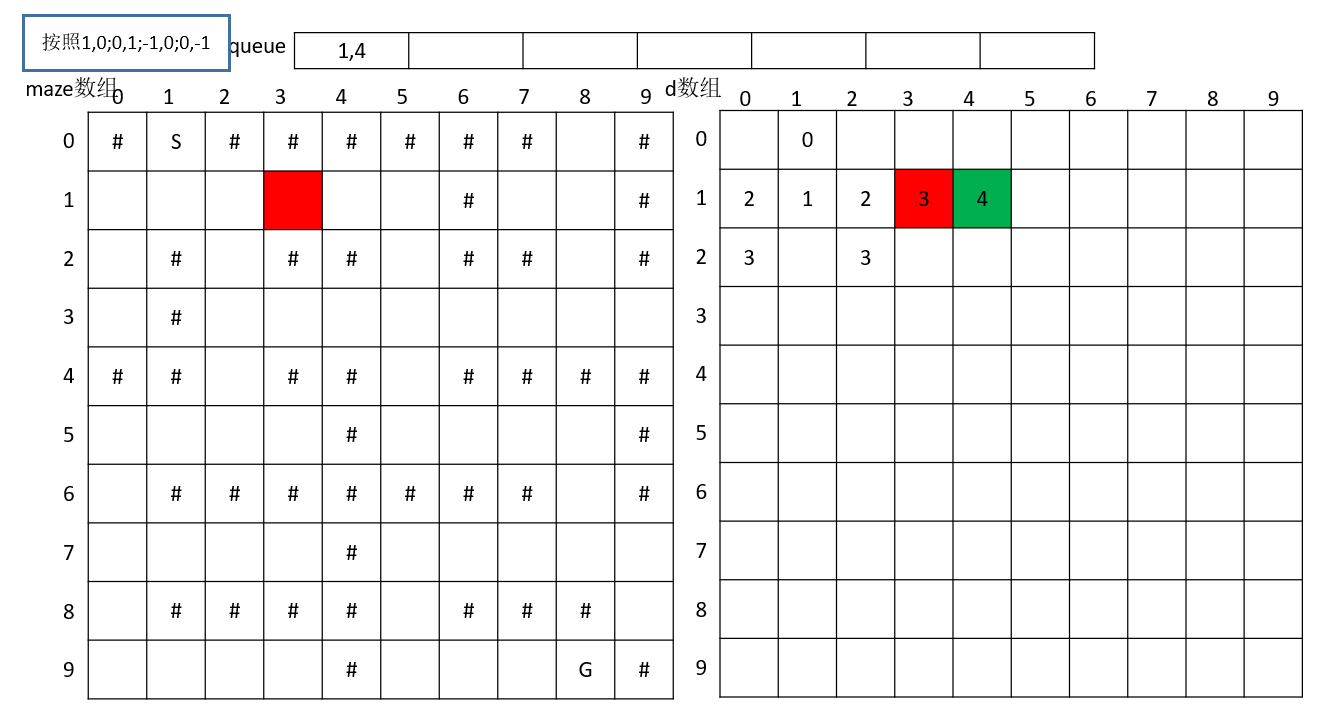
逆时针搜索下一个点,搜到(1,4)
以此类推,最终搜到(9,8)
3广度优先搜索算法框架
与深度优先搜索不同的是,广度优先搜索是按照层次遍历的,所以广度优先搜索不能像深度优先搜索一样使用递归来实现,广度优先搜索需要申请辅助队列来记录下一层需要遍历的节点
从一个起点出发到一个终点结束
1//单源的广度优先搜索
2int BFS(elemType start, elemType target) {
3 queue<elemType> q; //申请辅助队列
4 set<elemType> visited; //标记已访问过的,避免走回头路
5 q.push(start); //起点入队列
6 visited.insert(start); //标记起点
7 int step = 0; //记录步数
8 while (!q.empty()) {
9 int sz = q.size(); //每一层的元素个数
10 for (int i = 0; i < sz; i++) {
11 elemType cur = q.pop(); //获得队列中的元素
12 if (cur == target) { //判断是否需要结束搜索
13 return step;
14 }
15 for (elemType x : cur.neighbor()) { //确定下一层需要搜索的节点
16 if (visited.find(x) == visited.end()) {
17 q.push(x);
18 visited.insert(x);
19 }
20 }
21 }
22 step++; // 步数加一
23 }
24}