leetcode第53题，最大子数组和。采用动态规划来完成。

LeetCode 53最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

1输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
2输出：6
3解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

1输入：nums = [1]
2输出：1

示例 3：

1输入：nums = [5,4,-1,7,8]
2输出：23

提示：

  • 1 <= nums.length <= 105
  • -104 <= nums[i] <= 104

**进阶：**如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

思路

可以暴力求解，但是时间复杂度是o(n^2^)，不推荐

可以用动态规划的思想。

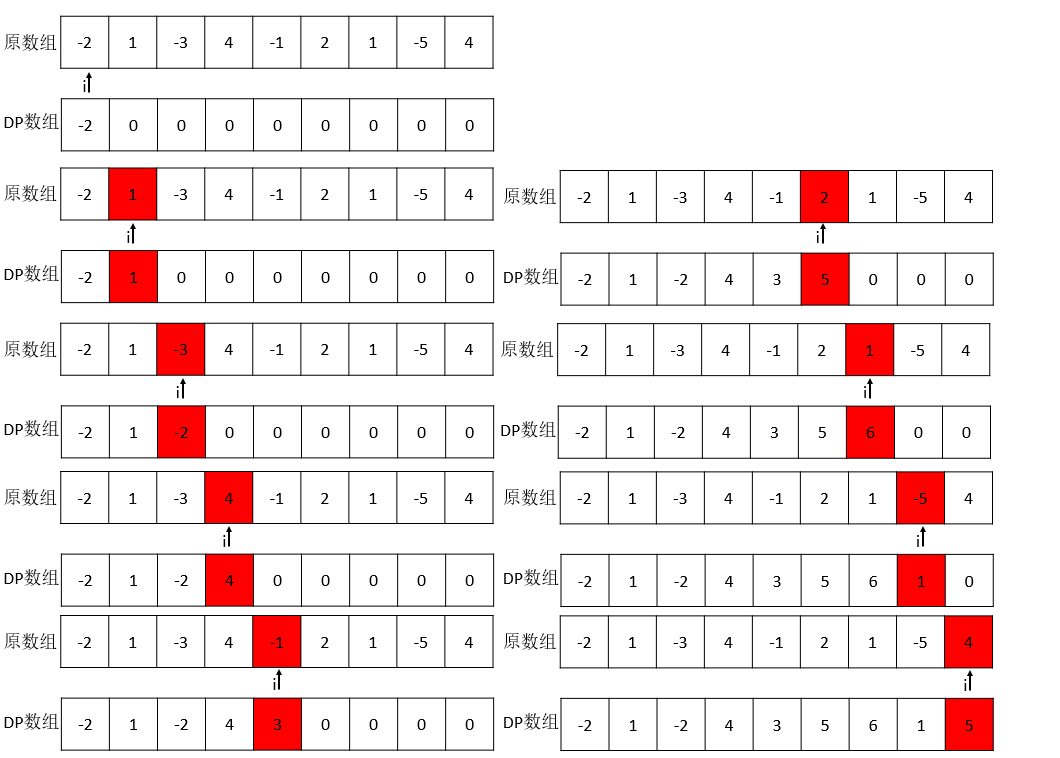
首先，这个的选择是当前元素是否加到前面子序列中，而这个选择会影响后面元素的大小。

1//DP[i]的定义，包括下标i之前的最大连续子序列和
2DP[i] = max(nums[i], (DP[i - 1] + nums[i]));

遍历一次就可以得到最大的子序列和，时间复杂度o(n)。

解题

 1class Solution {
 2    public int maxSubArray(int[] nums) {
 3        //动态规划的方式求解
 4        int numsLen = nums.length;
 5        int[] DP = new int[numsLen];
 6        //第一个元素，直接赋值即可，不需要在动态规划
 7        DP[0] = nums[0];
 8        //定一个变量收集最大值
 9        int max = DP[0];
10        for(int i = 1; i < numsLen; i++)
11        {
12            DP[i] = Math.max(nums[i],
13                             nums[i] + DP[i - 1]);
14            if(max < DP[i])
15            {
16                max = DP[i];
17            }
18        }
19        return max;
20    }
21}

改进版本，比一定需要DP数组，这个的DP数组元素只跟nums当前元素和DP的过去元素相关。将nums和DP合并成一个数组，也不会因此影响。

1DP[i] = max(nums[i], (DP[i - 1] + nums[i]));

解题改进

 1class Solution {
 2    public int maxSubArray(int[] nums) {
 3        //动态规划的方式求解,只需要使用一个nums数组
 4        //定一个变量收集最大值
 5        int max = nums[0];
 6        int pre = max;
 7        for(int i = 1; i < nums.length; i++)
 8        {
 9            pre = Math.max(nums[i],
10                           nums[i] + pre);
11            if(max < pre)
12            {
13                max = pre;
14            }
15        }
16        return max;
17    }
18}