leetcode第338题，比特位计数。采用位运算或者奇偶性来完成。

LeetCode 338比特位计数

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数 ，返回一个长度为 n + 1 的数组 ans 作为答案。

示例 1：

1输入：n = 2
2输出：[0,1,1]
3解释：
40 --> 0
51 --> 1
62 --> 10

示例 2：

1输入：n = 5
2输出：[0,1,1,2,1,2]
3解释：
40 --> 0
51 --> 1
62 --> 10
73 --> 11
84 --> 100
95 --> 101

提示：

  • 0 <= n <= 105

进阶：

  • 很容易就能实现时间复杂度为 O(n log n) 的解决方案，你可以在线性时间复杂度 O(n) 内用一趟扫描解决此问题吗？
  • 你能不使用任何内置函数解决此问题吗？（如，C++ 中的 __builtin_popcount ）

思路

使用位运算。

1//清除最低位的1
2x = x & (x - 1)

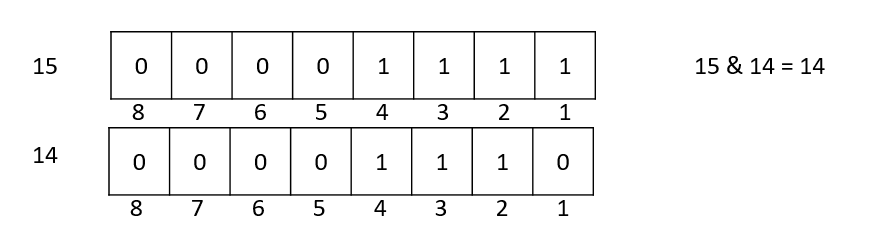
15跟14相比相差最低位的1

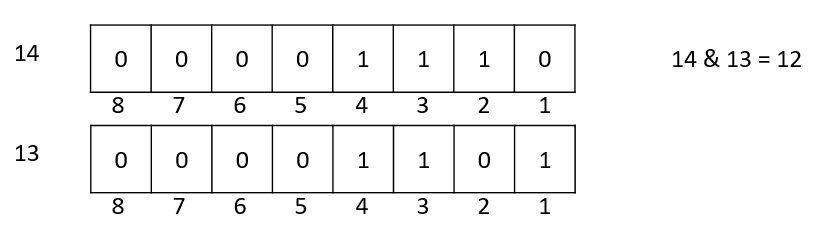
14跟12相比相差最低位的1

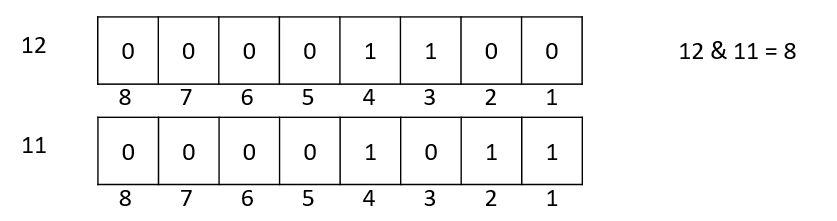
12跟8相比相差最低位的1

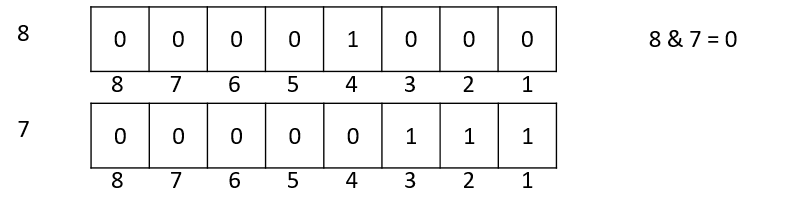
8跟0相比相差最低位的1

也就是说实际上15位中有几个1，可以是等价于14位中有几个1再加上1；同理14位中有几个1，可以是等价于12位中有几个1再加上1；12位中有几个1，可以是等价于8位中有几个1再加上1；8位中有几个1，可以是等价于0位中有几个1再加上1。

解题

 1class Solution {
 2    public int[] countBits(int n) {
 3        int[] bitArray = new int[n + 1];
 4        //初始值为0
 5        bitArray[0] = 0;
 6        for(int i = 1; i < n + 1; i++)
 7        {
 8            //有递归的思想
 9            bitArray[i] = bitArray[i & (i - 1)] + 1;
10        }
11        return bitArray;
12    }
13}

思路2

可以用奇偶的特性

 1//当奇数的时候
 2//9 1001
 3//8 1000
 4bitArray[i] = bitArray[i - 1];
 5//当偶数的时候
 6//例如
 7//8 1000
 8//4 0100
 9//2 0010
10//1 0001
11bitArray[i] = bitArray[i >> 1];

解题

 1class Solution {
 2    public int[] countBits(int n) {
 3        int[] bitArray = new int[n + 1];
 4        //初始值为0
 5        bitArray[0] = 0;
 6        for(int i = 1; i < n + 1; i++)
 7        {
 8            //使用奇偶性
 9            bitArray[i] = ((i & 1) == 1) ?
10                          bitArray[i - 1] + 1 :
11                          bitArray[i >> 1];
12        }
13        return bitArray;
14    }
15}