leetcode第121题，买卖股票的最佳时机。采用动态规划或者类似双指针来完成。

LeetCode 121买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

1输入：[7,1,5,3,6,4]
2输出：5
3解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
4注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

1输入：prices = [7,6,4,3,1]
2输出：0
3解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

  • 1 <= prices.length <= 105
  • 0 <= prices[i] <= 104

思路

可以跟之前的136题一样，使用暴力求解，但是不推荐。

这里可以使用动态规划。

这里可以看做把买股票作为一种亏损，买股票作为一种盈利。

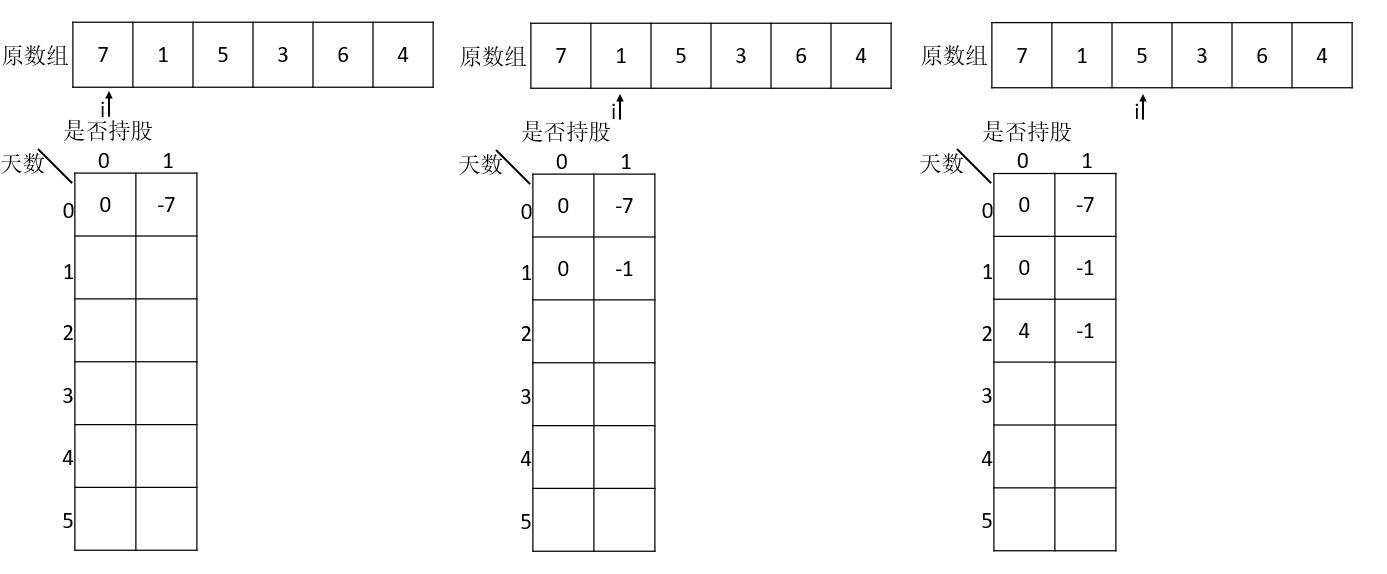
1//定义DP数组，其中i代表的是天数，j可以有0，代表不持有股票/或者股票卖出，j可以为1代表目前还持有股票。
2//DP[i][0],代表当前第i天不持有股票/或者股票卖出的总收益
3//DP[i][1],代表当前第i天持有股票的总收益(持有肯定是负的)
4DP[i][j]
5DP[i][0] = Math.max(DP[i - 1][0], DP[i - 1][1] + nums[i]);
6DP[i][1] = Math.max(DP[i - 1][1], -nums[i]);

解题

 1class Solution {
 2    public int maxProfit(int[] prices) {
 3        //判定是否满足要求
 4        if(prices.length < 2)
 5        {
 6            return 0;
 7        }
 8
 9        //用动态规划的方式，并且构造一个二位的DP数组
10        int[][] DP = new int[prices.length][2];
11        //初始化DP数组
12        DP[0][0] = 0;
13        DP[0][1] = -prices[0];//股票持有，那么就是负数
14        //从第二天开始遍历
15        for(int i = 1; i < prices.length; i++)
16        {
17            DP[i][0] = Math.max(DP[i - 1][0], DP[i - 1][1] + prices[i]);
18            DP[i][1] = Math.max(DP[i - 1][1], -prices[i]);
19        }
20        return DP[prices.length - 1][0];
21    }
22}

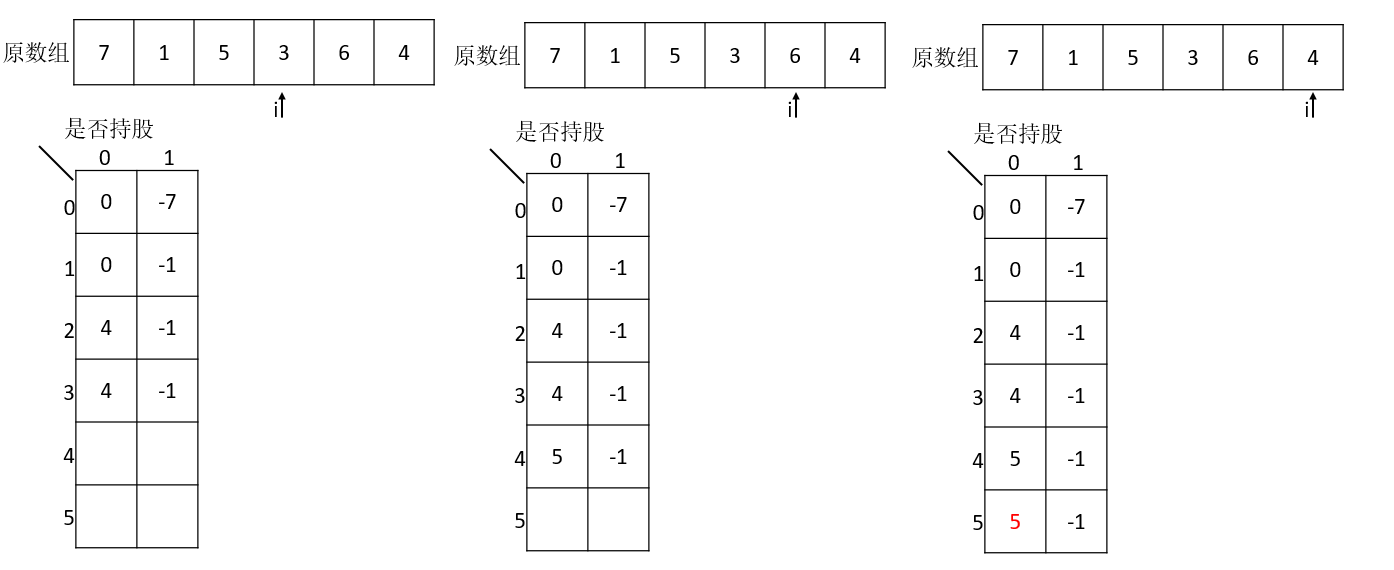
开始遍历数组来形成DP

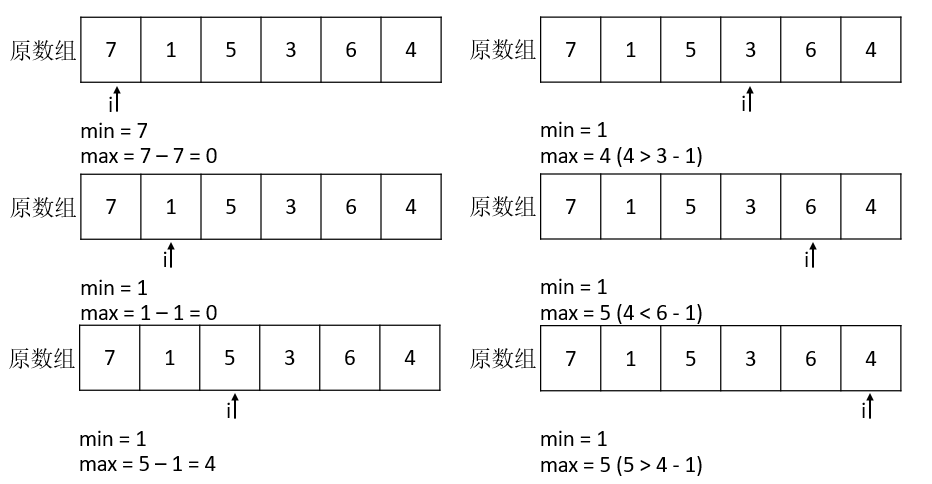
当然，买卖股票其实就是找到一个低位点，然后看低位点的某一高点的距离，距离最大即为最佳买卖点。

解题优化

 1class Solution {
 2    public int maxProfit(int[] prices) {
 3        //判定是否满足要求
 4        if(prices.length < 2)
 5        {
 6            return 0;
 7        }
 8        //类似双指针，使用遍历数组，指针A作为最小值，指针B用于和指针A保持最大距离
 9        int min = prices[0];
10        int max = 0;
11        for(int i = 1; i < prices.length; i++)
12        {
13            if(min > prices[i])
14            {
15                min = prices[i];
16            }else
17            {
18                max = Math.max(max, prices[i] - min);
19            }
20        }
21        return max;
22    }
23}