排序 8计数排序
500 Words|Read in about 3 Min|本文总阅读量次
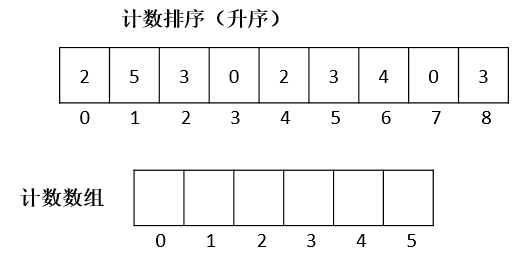
经典的排序算法,计数排序,用到了桶的概念
0准备
1//建立一个排序用的顺序表结构L
2#define MAXSIZE 9
3typedef struct SqList
4{
5 int r[MAXSIZE];
6 int length;
7}SqList;
8/*排序的交换函数*/
9void swap(SqList* L,int i,int j)
10{
11 int temp = L->r[i];
12 L->r[i] = L->r[j];
13 L->r[j] = temp;
14}
计数排序(count Sort)
一个排序时不比较元素大小的排序算法。
计数排序对一定范围内的整数排序时候的速度非常快,一般快于其他排序算法。但计数排序局限性比较大,只限于对整数进行排序,而且待排序元素值分布较连续、跨度小的情况。
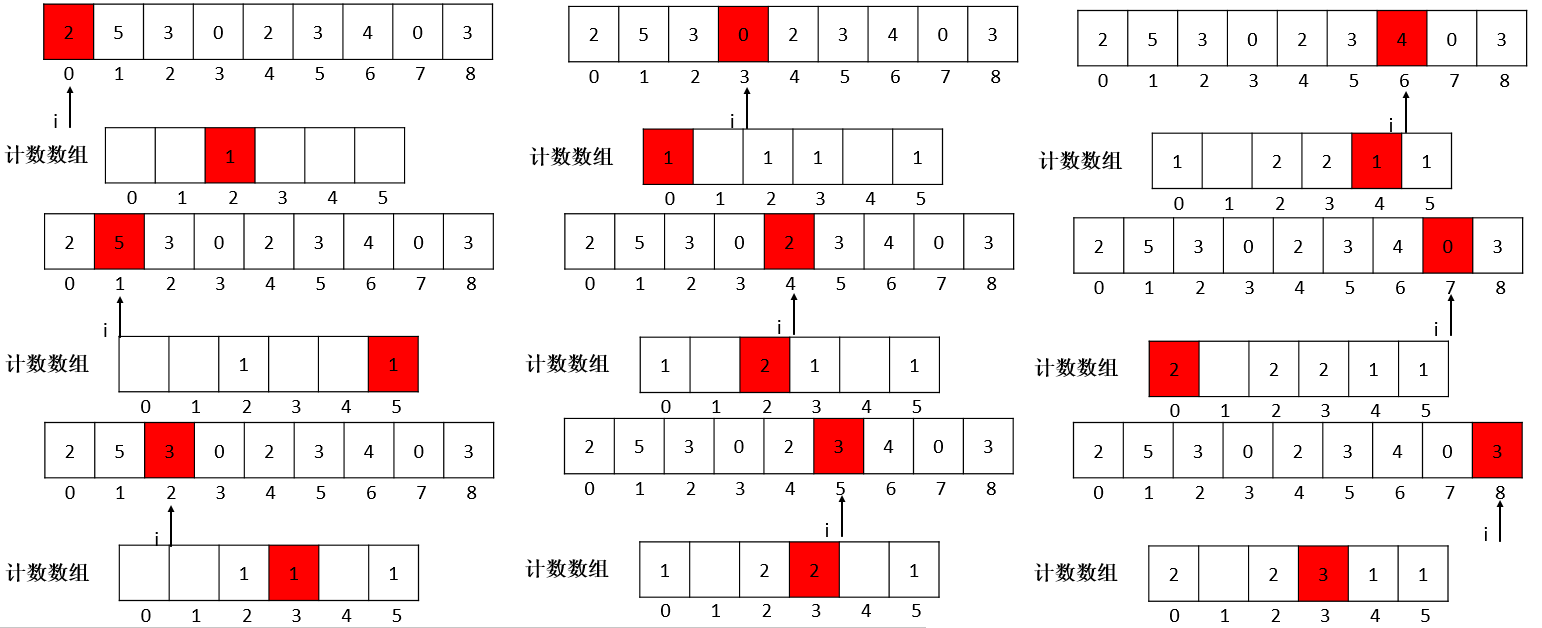
如果一个数组里所有元素都是整数,而且都在0-K以内。那对于数组里每个元素来说,如果能知道数组里有多少项小于或等于该元素,就能准确地给出该元素在排序后的数组的位置。
C的版本
1void CountSort(SqList *L) {
2 int bias, min = L->r[0], max = L->r[0];
3 for(int i = 0; i < L->length; i++) {
4 if (L->r[i] > max) {
5 max = L->r[i];
6 }
7 if (L->r[i] < min) {
8 min = L->r[i];
9 }
10 }
11 bias = 0 - min;
12 //初始化计数数组
13 int* countArray= new int[max - min + 1];
14 memset(countArray, 0x0, sizeof(int) * (max - min + 1));
15 //遍历整个原始数组,将原始数组中每个元素值转化为计数数组下标,并将计数数组下标对应的元素值大小进行累加
16 for(int i = 0; i < L->length; i++)
17 {
18 countArray[L->r[i] + bias]++;
19 }
20
21 int index = 0;//访问原始数组时的下标计数器
22 int i = 0;//访问计数数组时的下标计数器
23 //访问计数数组,将计数数组中的元素转化后,重新写回原始数组
24 while(index < L->length)
25 {
26 //只要计数数组中当前下标元素的值不为0,就将计数数组中的元素转换后,重新写回原始数组
27 if(countArray[i] > 0)
28 {
29 L->r[index] = i - bias;
30 countArray[i]--;
31 index++;
32 }else
33 {
34 i++;
35 }
36 }
37 delete[] countArray;
38}
Java代码
1public int[] CountSort(int[] sourceArray) throws Exception {
2 // 对 arr 进行拷贝,不改变参数内容
3 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
4
5 int maxValue = getMaxValue(arr);
6
7 return countingSort(arr, maxValue);
8}
9
10private int[] countingSort(int[] arr, int maxValue) {
11 int bucketLen = maxValue + 1;
12 //计数数组初始化
13 int[] bucket = new int[bucketLen];
14
15 for (int value : arr) {
16 bucket[value]++;
17 }
18
19 int sortedIndex = 0;
20 for (int j = 0; j < bucketLen; j++) {
21 while (bucket[j] > 0) {
22 arr[sortedIndex++] = j;
23 bucket[j]--;
24 }
25 }
26 return arr;
27}
28
29private int getMaxValue(int[] arr) {
30 int maxValue = arr[0];
31 for (int value : arr) {
32 if (maxValue < value) {
33 maxValue = value;
34 }
35 }
36 return maxValue;
37}
改良版本,用到了最大最小值
1public int[] CountSort(int[] nums)
2{
3 if(0 == nums.length) return nums;
4 //寻找数组中最大值,最小值
5 //bias偏移量,用以定位原始数组每个元素在计数数组中的下标位置
6 int bias, min = nums[0], max = nums[0];
7 for(int i = 1; i < nums.length; i++)
8 {
9 if(nums[i] > max)
10 {
11 max = nums[i];
12 }
13 if(nums[i] < min)
14 {
15 min = nums[i];
16 }
17 bias = 0 - min;
18 //获取计数数组的容量
19 int[] countArray = new int[max - min + 1];
20 Array.fill(counterArray, 0);
21 //遍历整个原始数组,将原始数组中每个元素值转化为计数数组下标,并将计数数组下标对应的元素值大小进行累加
22 for(int i = 0; i < nums.length; i++)
23 {
24 countArray[nums[i] + bias]++;
25 }
26 PrintArray.print(countArray);
27 int index = 0;//访问原始数组时的下标计数器
28 int i = 0;//访问计数数组时的下标计数器
29 //访问计数数组,将计数数组中的元素转化后,重新协会原始数组
30 while(index < nums.length)
31 {
32 //只要计数数组中当前下标元素的值不为0,九江计数数组中的元素转换后,重新写回原始数组
33 if(countArray[i] != 0)
34 {
35 nums[index] = i - bias;
36 countArray[i]--;
37 index++;
38 }else
39 {
40 i++;
41 }
42 PrintArray.print(countArray);
43 }
44 }
45}
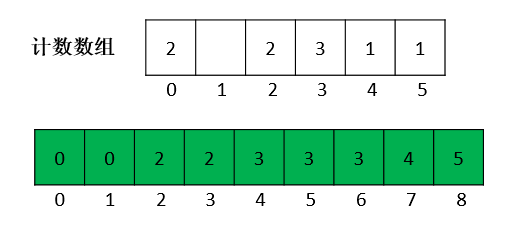
计数数组的遍历
最终得到
实际应用
我们会同时找出数组中的
max和min,主要是为了尽量节省空间。试想[1003,1001,1030,1050]这样的数据要排序,真的需要建立长度为1050+1的数组吗?我们只需要长度为1050-1003+1=48的数组(先不考虑额外+1的长度),就能囊括从最小到最大元素之间的所有元素了。如果待排序数组的元素值跨度很大,比如[99999,1,2],为三个元素排序要使用99999-1+1的空间,实在是浪费。所以计数排序适用于待排序元素值分布较连续、跨度小的情况。