排序 7堆排序
400 Words|Read in about 2 Min|本文总阅读量次
经典的排序算法,堆排序
0准备
1//建立一个排序用的顺序表结构L
2#define MAXSIZE 9
3typedef struct SqList
4{
5 int r[MAXSIZE];
6 int length;
7}SqList;
8/*排序的交换函数*/
9void swap(SqList* L,int i,int j)
10{
11 int temp = L->r[i];
12 L->r[i] = L->r[j];
13 L->r[j] = temp;
14}
堆排序HeapSort
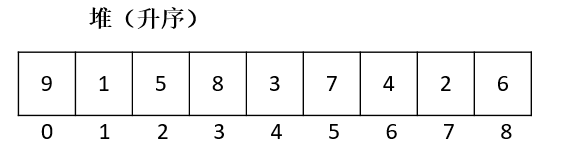
许多应用程序都需要处理有序的元素,但不一定要求他们全部有序,或者不一定要一次就将他们排序,很多时候,我们每次只需要操作数据中的最大元素(最小元素),那么有一种基于二叉堆的数据结构可以提供支持。
所谓二叉堆,是一个完全二叉树的结构,同时满足堆的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。在一个二叉堆中,根节点总是最大(或者最小)节点,这样堆我们称之为最大(小)堆。
堆排序算法就是抓住了这一特点,每次都取堆顶的元素,然后将剩余的元素重新调整为最大
〔最小)堆,依次类推,最终得到排序的序列。
C的版本
1void HeapAdjust(SqList *L, int node, int end);
2void HeapSort(SqList *L)
3{
4 int i;
5 for(i = L->length / 2 - 1; i > 0; i--)
6 {
7 HeapAdjust(L,i,L->length - 1);/*把L中的r构建成一个大顶堆*/
8 }
9
10 for(i = L->length - 1; i > 0; i--)
11 {
12 swap(L, 0, i);
13 HeapAdjust(L, 0, i - 1);/*将L->r[1..1-1]重新调整为大顶堆*/
14 }
15}
16/*本函数调整L->r[node]的关键字,使L->r[node..end]成为一个大顶堆*/
17void HeapAdjust(SqList *L, int node, int end)
18{
19 int j,temp;
20 temp = L->r[node];
21 for(j = 2 * node + 1; j <= end; j = j * 2 + 1)
22 {
23 if(j < end && L->r[j] < L->r[j + 1])/*j<end是判断是否有右孩子*/
24 {
25 j++;
26 }
27
28 if(temp >= L->r[j])
29 {
30 //说明大顶堆已经在这个node结点排列好了
31 break;
32 }
33 //node的值换成node的左右孩子的较大值,那么需要调整交换的孩子对应的堆,重新生成大顶堆
34 L->r[node] = L->r[j];
35 node = j;
36 }
37 L->r[node] = temp;/*node为全局变量,temp包含两个意思一个是直接break另外一个是L->r[j]*/
38}
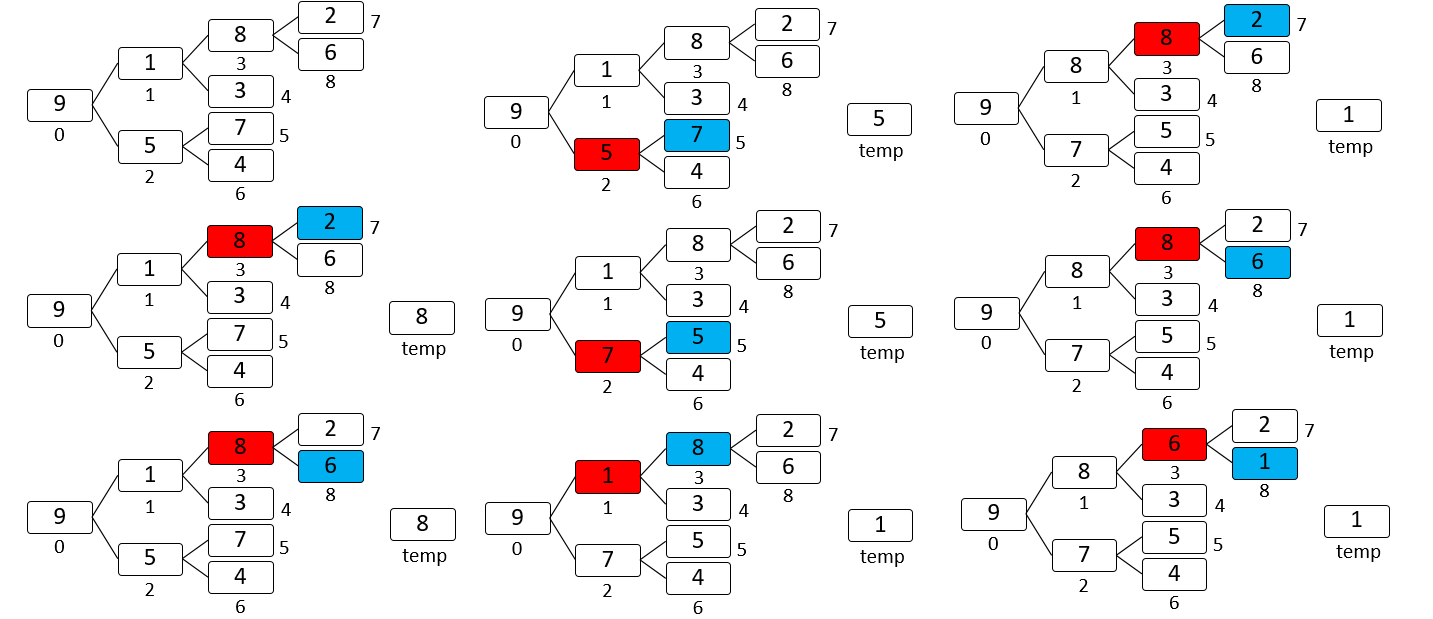
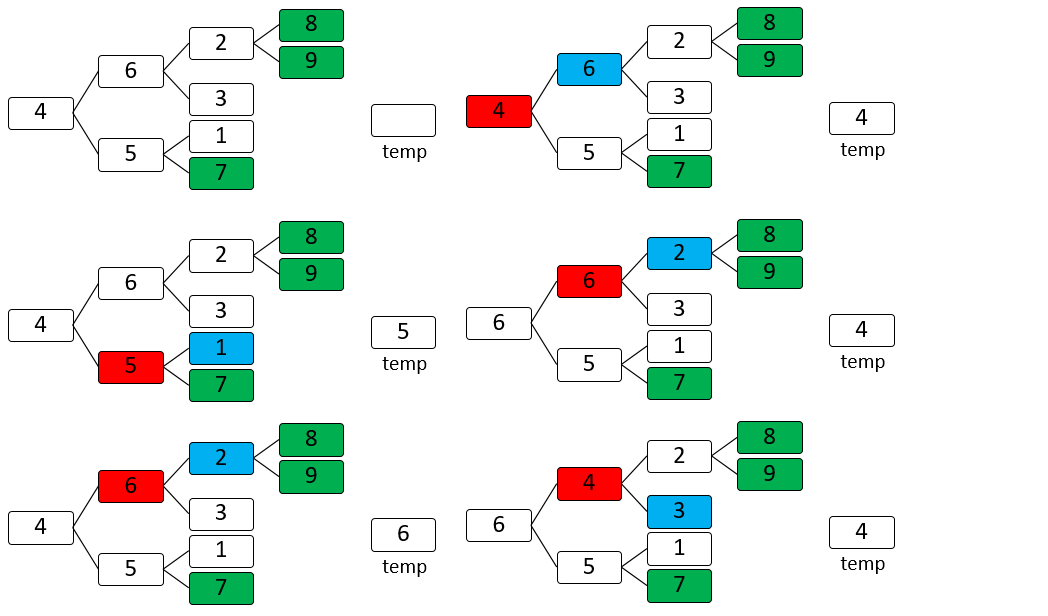
堆排序(Heap Sort)就是利用堆(假设利用大顶堆)进行排序的方法。它的基本思想是,将待排序的序列构造成一个大顶堆。此时,整个序列的最大值就是堆顶的根结点。将它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素中的次小值。如此反复执行,便能得到一个有序序列了。
中心思想:不断的构成大顶堆的过程(二叉树)
大顶堆第一个数9
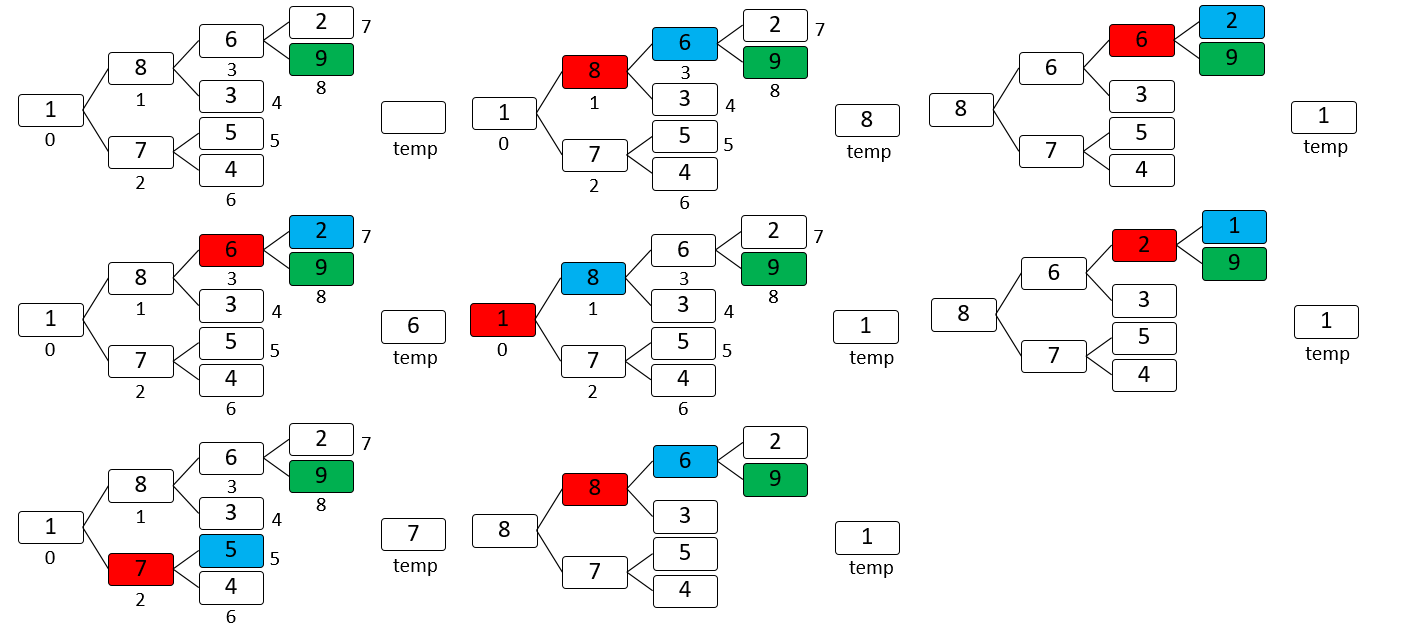
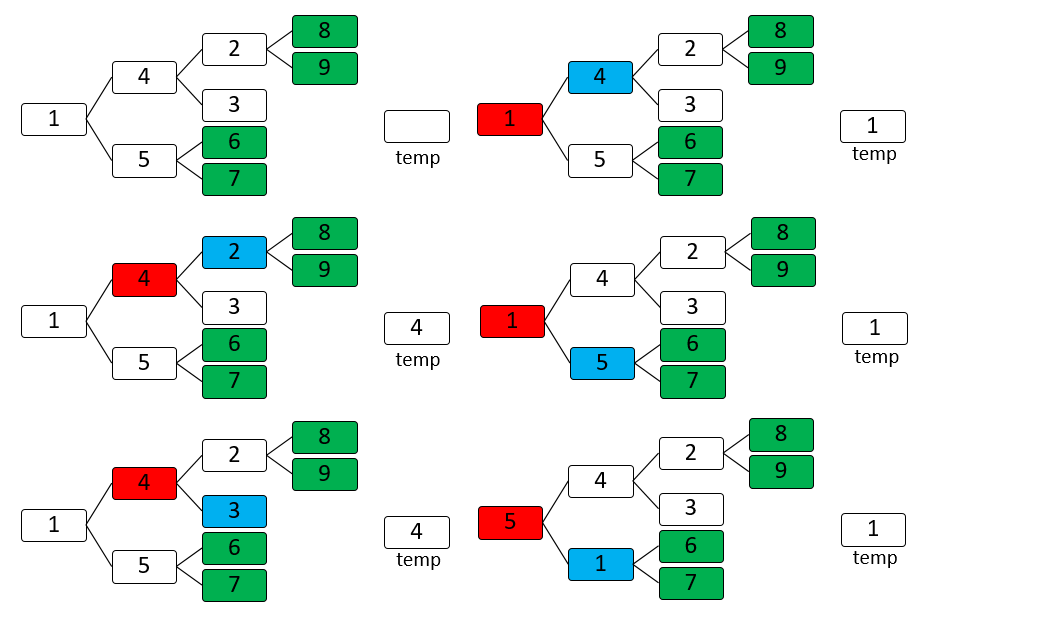
大顶堆第二个数8
大顶堆第三个数7
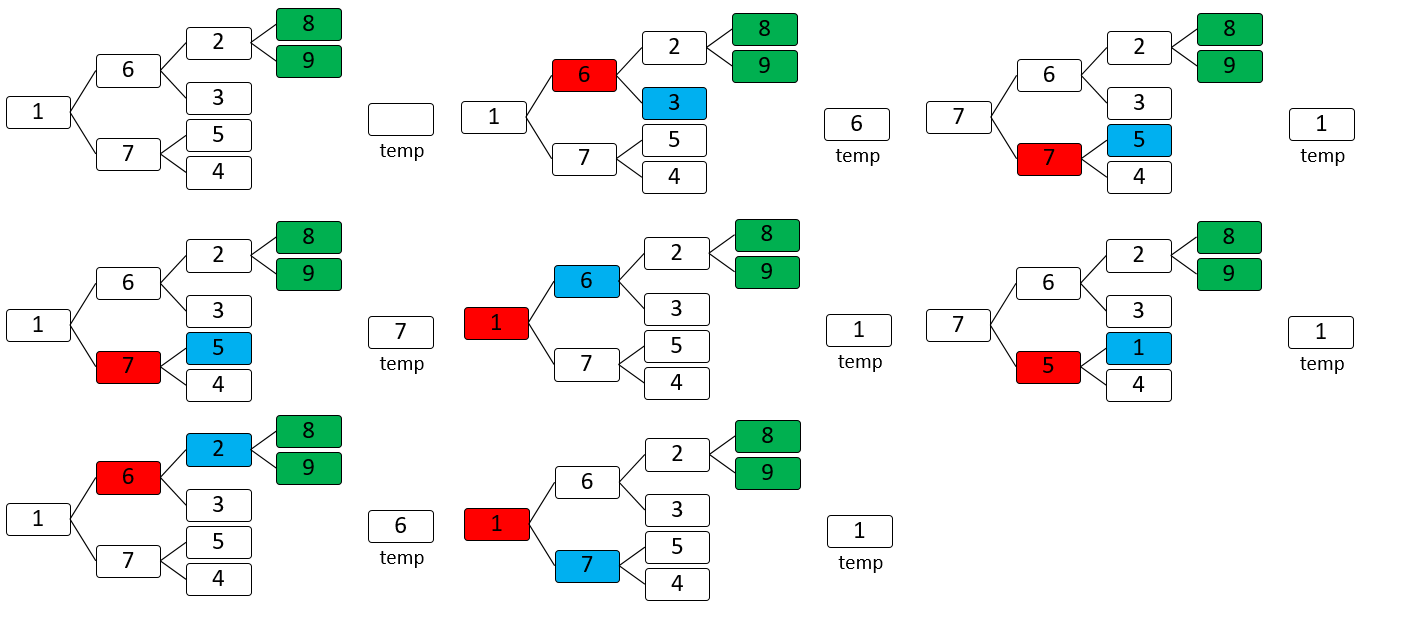
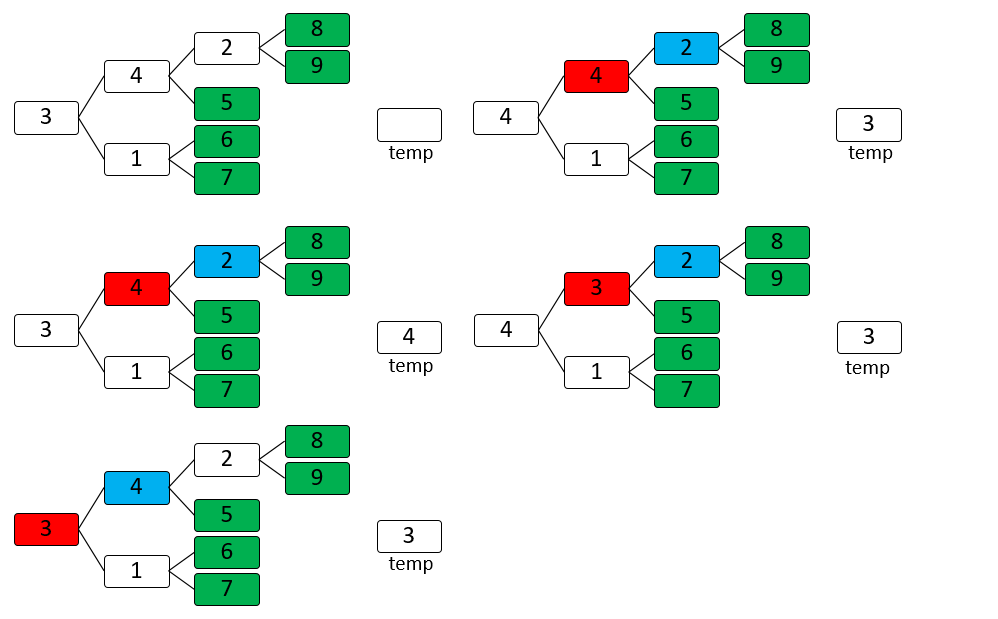
大顶堆第四个数6
大顶堆第四个数5
大顶堆第五个数4
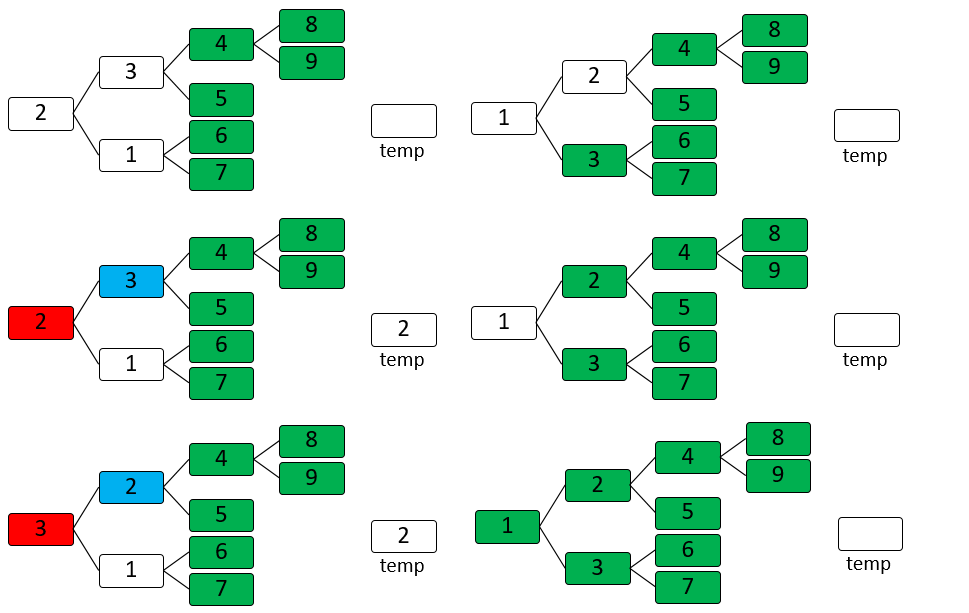
大顶堆最后三个数1,2,3
Java版本
1public int[] HeapSort(int[] nums)
2{
3 len = nums.length;
4 if(len < 1) return nums;
5 //构建一个最大堆
6 buildMaxHeap(nums);
7 //循环将堆首(最大值)与为排序数据末位交换,然后调整为最大堆
8 while(len > 0)
9 {
10 swap(nums, 0, len -1);
11 len--;
12 adjustHeap(nums, 0);
13 PrintArray.print(nums);
14 }
15 return nums;
16}
17
18//建立最大堆
19public static void buildMaxHeap(int[] array)
20{
21 for(int i = len / 2 - 1; i > 0; i--)
22 {
23 adjustHeap(array, i);
24 }
25 System.out.println("构造完成最大堆");
26}
27
28//调整使之成为最大堆
29public static void adjustHeap(int[] array, int i)
30{
31 int maxIndex = i;
32 int left = 2 * i + 1;
33 int right = 2* i + 2;
34 //如果有左子树,且左子树大于父节点,则将最大指针指向左子树
35 if(left < len && array[left] > array[maxIndex])
36 {
37 maxIndex = left;
38 }
39 //如果有右子树,且右子树大于父节点且大于左子树,则将最大指针指向右子树
40 if(right < len && array[right] > array[maxIndex] && array[right] > array[left])
41 {
42 maxIndex = right;
43 }
44 //如果父节点不是最大值,则将父节点与最大值交换,并且递归吊证与父节点交换的位置
45 if(maxIndex != i)
46 {
47 swap(array, maxIndex, i);
48 PrintArray.print(array);
49 adjustHeap(array, maxIndex);
50 }
51}