排序 6归并排序
800 Words|Read in about 4 Min|本文总阅读量次
经典的排序算法,归并排序
0准备
1//建立一个排序用的顺序表结构L
2#define MAXSIZE 9
3typedef struct SqList
4{
5 int r[MAXSIZE];
6 int length;
7}SqList;
8/*排序的交换函数*/
9void swap(SqList* L,int i,int j)
10{
11 int temp = L->r[i];
12 L->r[i] = L->r[j];
13 L->r[j] = temp;
14}
归并排序MergeSort
归并排序
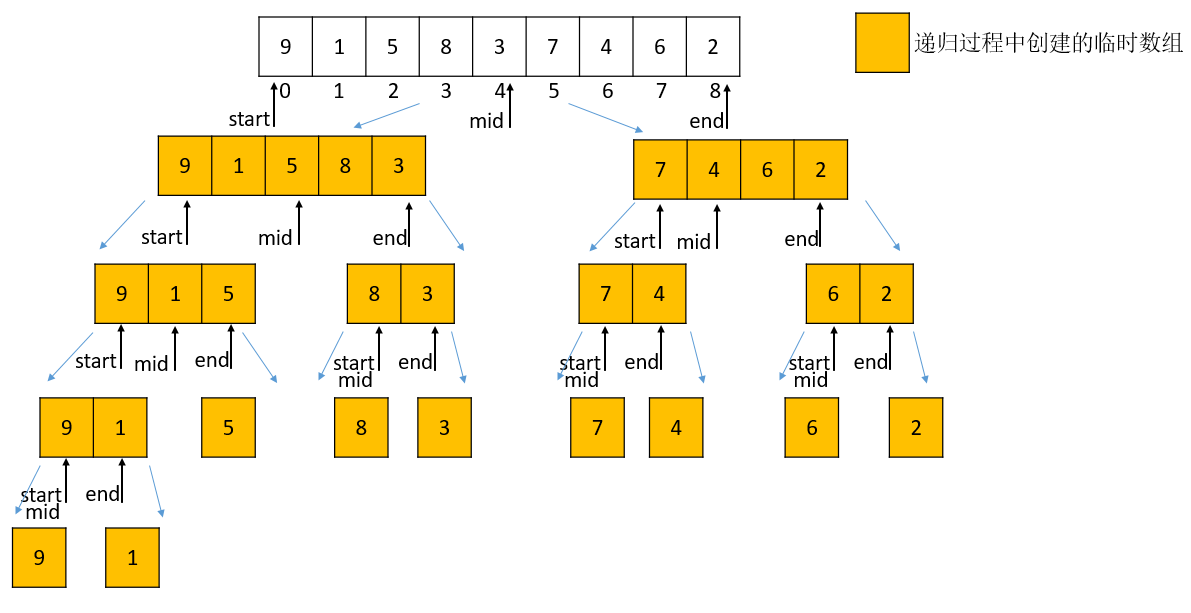
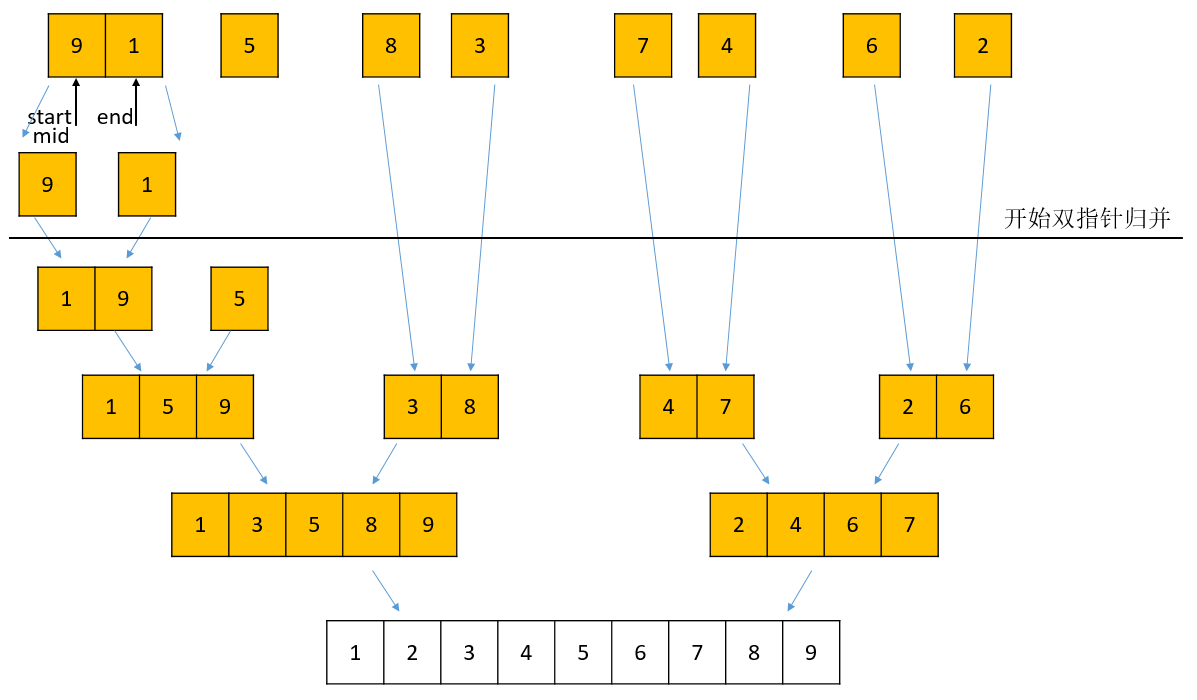
归并排序(Merging Sort)就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列的长度为1,然后两两归并,得到⌈ n / 2 ⌉ \lceil n/2 \rceil⌈n/2⌉(⌈ x ⌉ \lceil x \rceil⌈x⌉)表示不小于x的最小整数)个长度为2或1的有序子序列;再两两归并,……,如此重复,直至得到一个长度为n的有序序列为止,这种排序方法称为2路归并排序。
C的版本
1void MSort(int src[], int des[], int start, int end);
2void Merge(int partSrc[], int partDes[], int partStart, int partMid, int partEnd);
3/*递归调用,向外封装了一个函数*/
4void MergeSort(SqList *L)
5{
6 MSort(L->r, L->r, 0, L->length - 1);
7}
8/*将src[start..end]归并排序为des[start..end]*/
9void MSort(int src[], int des[], int start, int end)
10{
11 int mid;
12 int tmp[MAXSIZE+1];//每次递归归并的时候都会新创建一个数组
13 if(start == end)
14 des[start] = src[start];
15 else
16 {
17 mid = (start + end) >> 1;
18 MSort(src, tmp, start, mid);
19 MSort(src, tmp, mid + 1, end);
20 Merge(tmp, des, start, mid, end);
21 }
22}
23/*将有序的partSrc[partStart..partMid]和partSrc[partMid+1..partEnd]归并为有序的TR[partStart..partEnd]*/
24void Merge(int partSrc[], int partDes[], int partStart, int partMid, int partEnd)
25{
26 int partMidPos, partDesPos, l;
27 /*这里不用||代替&&原因是为了防止数组越界,由于partStart++和partMidPos++*/
28 /*这里用到双指针的思想,两个指针分别为partStart和partMidPos,原数组为partSrc,目标数组为partDes*/
29 for(partMidPos = partMid + 1, partDesPos = partStart; partStart <= partMid && partMidPos <= partEnd; partDesPos++)
30 {
31 if(partSrc[partStart] < partSrc[partMidPos])
32 partDes[partDesPos] = partSrc[partStart++];
33 else
34 partDes[partDesPos] = partSrc[partMidPos++];
35 }
36 /*不可省,主要为了防止数组越界,导致partStart和partMidPos在partSrc数组赋值到partDes上出现混乱*/
37 if(partStart <= partMid)
38 {
39 for(l = 0; l <= partMid - partStart; l++)/*这里是L不是数字1*/
40 partDes[partDesPos + l] = partSrc[partStart + l];
41 }
42 if(partMidPos <= partEnd)
43 {
44 for(l = 0; l <= partEnd - partMidPos; l++)
45 partDes[partDesPos + l] = partSrc[partMidPos + l];
46 }
47}
Java版本
1public int[] MergeSort(int[] nums)
2{
3 if(nums.length < 2) return nums;
4 int mid = nums.length / 2;
5 int[] left = Arrays.copyOfRange(nums, 0, mid);
6 int[] right = Arrays.copyOfRange(nums, mid, nums.length);
7 return merge(MergeSort(left), MergeSort(right));
8}
9//将两端排序好的数组结合成一个排序数组,双指针
10public static int[] merge(int[] left, int[] right)
11{
12 int[] result = new int[left.length + right.length];
13 for(int index = 0, i = 0, j = 0; index < result.length; index++)
14 {
15 //左边数组已经取完,完全取右边数组的值即可
16 if(i >= left.length)
17 {
18 result[index] = right[j++];
19 //右边数组已经取完,完全取左边数组的值即可
20 }else if(j >= right.length)
21 {
22 result[index] = left[j++];
23 //左边数组元素大于右边数组,取右边元素
24 }else if(left[i] < right[j])
25 {
26 result[index] = right[j++];
27 //右边数组元素大于左边数组,取左边元素
28 }else
29 {
30 result[index] = left[j++];
31 }
32 }
33}
TimSort
除了上述的归并,还存在另一种更加优化的归并排序,称为TimSort,结合了合并排序(合并排序)和插入排序(插入排序)而得出的排序算法,它在现实中有很好的效率.Tim Peters在2002年设计了该算法并在Python中使用是Python中list.sort的默认实现)。该算法找到数据中已经排好序的块 - 分区,每一个分区叫一个run,然后按规则合并这些run.Pyhton自从2.3版本以后一直采用Timsort算法排序,现在Java SE7和Android也采用Timsort算法对数组排序。JDK1.8中的实现,如下所示
1static <T> void sort(T[] a, int lo, int hi, Comparator<? super T> c,
2 T[] work, int workBase, int workLen) {
3 assert c != null && a != null && lo >= 0 && lo <= hi && hi <= a.length;
4
5 int nRemaining = hi - lo;
6 if (nRemaining < 2)
7 return; // Arrays of size 0 and 1 are always sorted
8
9 // 数组长度小于MIN_MERGER,不进行归并处理
10 if (nRemaining < MIN_MERGE) {
11 // 从lo位置开始找出有序的序列,如果是倒序装换为正序
12 int initRunLen = countRunAndMakeAscending(a, lo, hi, c);
13 // 二分插入排序,lo+iniRunLen为起始位置(因为这之前的都是有序且正序的)
14 binarySort(a, lo, hi, lo + initRunLen, c);
15 return;
16 }
17
18 /**
19 *实例化TimSort对象
20 * March over the array once, left to right, finding natural runs,
21 * extending short natural runs to minRun elements, and merging runs
22 * to maintain stack invariant.
23 */
24 TimSort<T> ts = new TimSort<>(a, c, work, workBase, workLen);
25 // run最小长度
26 int minRun = minRunLength(nRemaining);
27 do {
28 // Identify next run
29 int runLen = countRunAndMakeAscending(a, lo, hi, c);
30
31 // run长度小于minRun,使用插入法进行补充
32 if (runLen < minRun) {
33 int force = nRemaining <= minRun ? nRemaining : minRun;
34 binarySort(a, lo, lo + force, lo + runLen, c);
35 runLen = force;
36 }
37
38 // 将run推入栈中,并判断是否需要合并
39 ts.pushRun(lo, runLen);
40 ts.mergeCollapse();
41
42 // Advance to find next run
43 lo += runLen;
44 nRemaining -= runLen;
45 } while (nRemaining != 0);
46
47 // 循环结束,将栈中剩余的序列合并
48 assert lo == hi;
49 ts.mergeForceCollapse();
50 assert ts.stackSize == 1;
51}
52
53/*当数组长度小于MIN_MERGE,直接返回数组长度,相当不做归并排序只进行插入排序,与上述对MIN_MERGE判断一致。
54如果数组长度是2的精准乘方(2^m,2的阶乘),返回MIN_MERGE/2
55其余返回整数k,MIN_MERGE/2 <= K <= MIN_MERGE,n/k接近但严格小于2的精准乘方。(严格小于即差值为1)*/
56private static int minRunLength(int n) {
57 assert n >= 0;
58 int r = 0; // Becomes 1 if any 1 bits are shifted off
59 while (n >= MIN_MERGE) {
60 r |= (n & 1); // 奇数二进制低位为1,&1=1;偶数二进制低位为0,&1=0
61 n >>= 1; // 向右移一位,相当于除以2
62 }
63 return n + r;
64}
当待排序数组长度小于MIN_MERGER且已经是有序时,只进行一次查找有序序列的过程(countRunAndMakeAscending),是对数组的一次遍历,此时不需要进行二分插入排序也不需要进行归并。即最好情况下TimSort的时间复杂度为O(n)。
平均来看,使用了二分插入排序和归并排序,TimSort的时间复杂度为O(n*logn)。
在归并的过程使用了临时数组tmp存放待比对移动的元素,其空间复杂度为O(n)。
在二分插入即归并的过程中,对于大小相同的元素,没有改变其先后顺序,因此TimSort是一种稳定的排序算法。
快速排序的平均时间复杂度也为O(n*logn),但快速排序是一种不稳定的排序,无法保证排序前后相同大小元素的有序性,这在某些场景下会出现影响,具体点击这里。