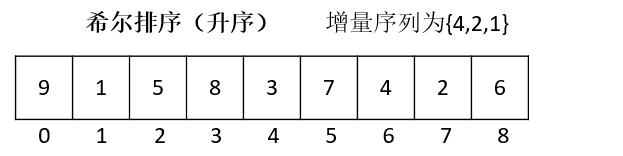
排序 5希尔排序
300 Words|Read in about 2 Min|本文总阅读量次
经典的排序算法,希尔排序
0准备
1//建立一个排序用的顺序表结构L
2#define MAXSIZE 9
3typedef struct SqList
4{
5 int r[MAXSIZE];
6 int length;
7}SqList;
8/*排序的交换函数*/
9void swap(SqList* L,int i,int j)
10{
11 int temp = L->r[i];
12 L->r[i] = L->r[j];
13 L->r[j] = temp;
14}
1希尔排序(ShellSort))
一种基于插入排序的快速的排序算法。简单插入排序对于大规模围序数组很慢,因为元素只能一点一点地从数组的一端移动到另一端。 希尔排序为了加快速度简单地改进了插入排序,也称为缩小增量排序,同时该算法是冲破o(n^2)的第一批算法之一。
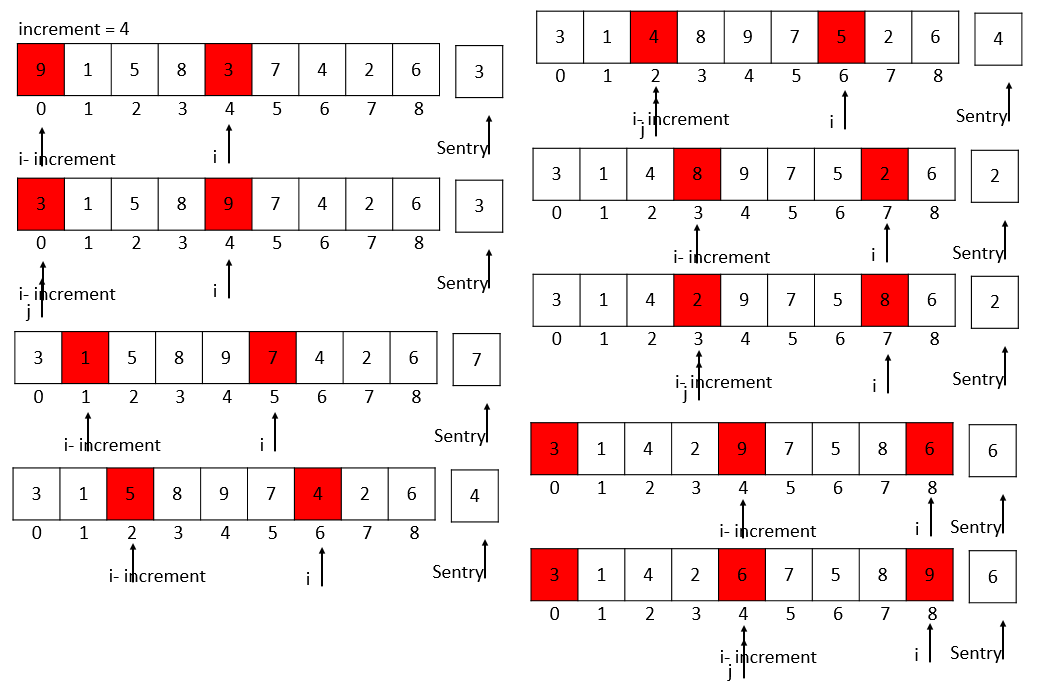
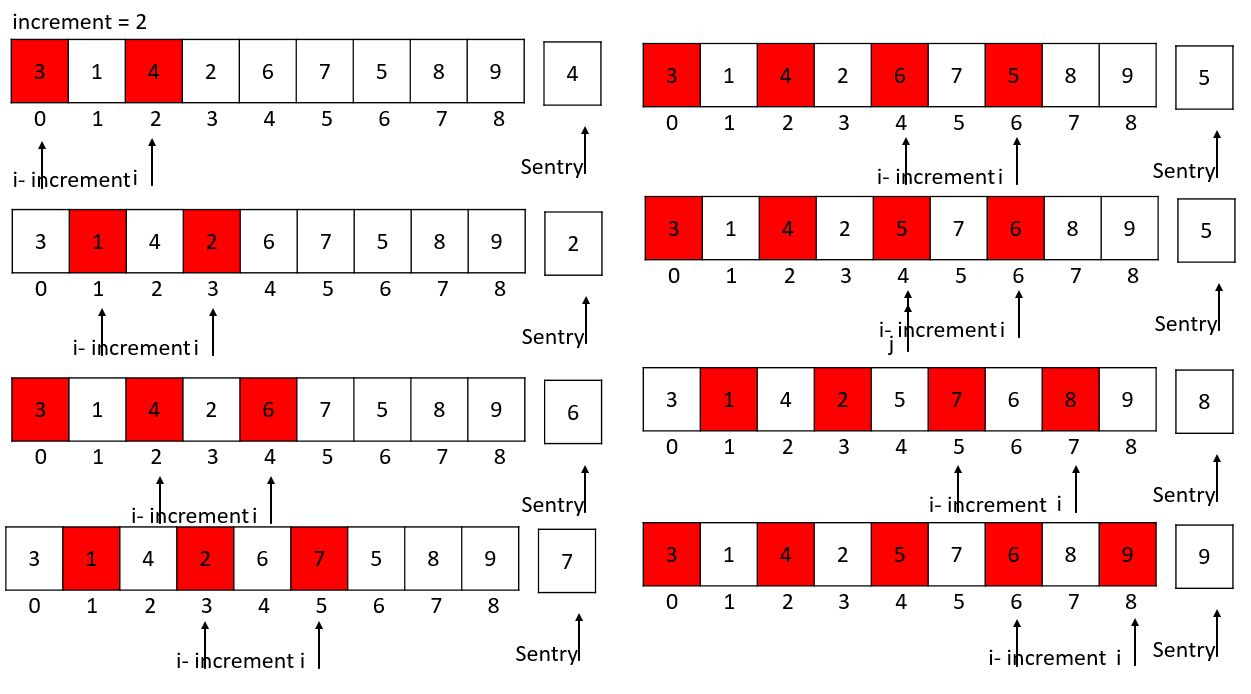
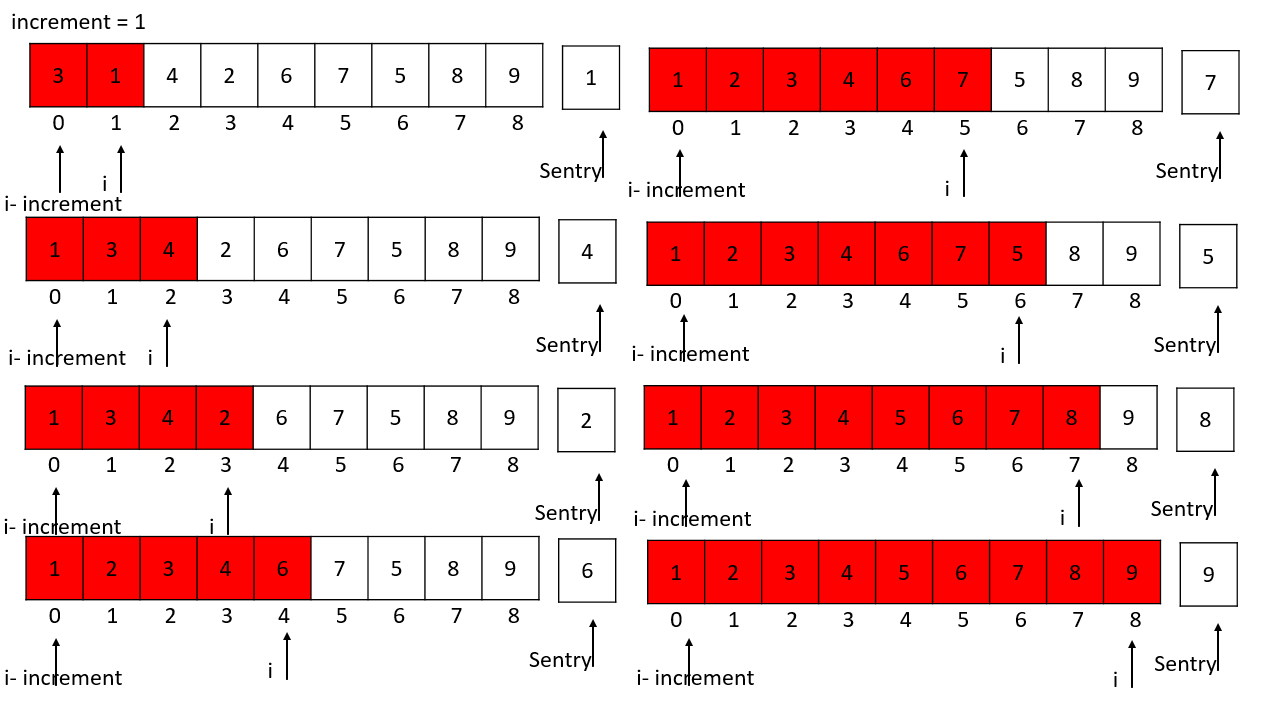
希尔排序是把记录按下表的一定增量分组,对每组使用直接插入排序算法排序;然后缩小增星继续分组排序,随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组。再次排序,完成整个数组的排序。这个不断缩小的增量,就构成了一个增量序列。
在直接插入排序的基础上,我们需要采取跳跃分割的策略: 增加increment,比如increment=increment / 3 + 1
C的版本
1void ShellSort(SqList *L)
2{
3 int i = 0, j = 0;
4 int increment = L->length;
5 do
6 {
7 increment = increment / 3 + 1;
8 for(i = increment; i < L->length; i++)
9 {
10 if(L->r[i] < L->r[i - increment])
11 {
12 int Sentry = L->r[i];/*设置哨兵*/
13 for(j = i - increment; j >= 0 && L->r[j] > Sentry; j -= increment)
14 {
15 L->r[j + increment] = L->r[j];
16 }
17 L->r[j + increment] = Sentry;
18 }
19 }
20 } while (increment > 1);
21}
increment = 4
increment = 2
increment = 1
从理论上说,只要一个数组是递减的,并且最后一个值是1,都可以作为增量序列使用。有没有一个步长序列,使得排序过程中所需的比较和移动次数相对较少,并且无论待排序列记录数有多少,算法的时间复杂度都能新近最佳呢?但是目前从数学上来说,无法证明某个序列是"最好的”。
常用的增量序列
希尔增量序列(折半序列):{N/2,(N/2)/2,,),其中N为原始数组的长度,这是最常用的序列,但却不是最好的
Hibbard序列:{2^k^-1,…,3,1)
Sedgewick序列:{.,109,41,19,5,1)表达式为19*4-9*2+1或者4-3*2+1
Java版本
1public int[] ShellSort(int[] nums)
2{
3 int len = nums.length;
4 //按照增量分组后,每个分组中,tmp爱表当前待排徐数据,钙元素之前的组内元素已被排序过
5 int currentValue, gap = len / 2;
6 while(gap > 0)
7 {
8 for(int i = 0; i < len; i++)
9 {
10 currentValue = nums[i];
11 //组内已被排序数据的索引
12 int preIndex = i - gap;
13 //在组内被排序过数据中倒序寻找合适的位置,如果当前待排序数据比比较的元素小,则将比较的元素再组内后移一位
14 while(preIndex >= 0 && nums[preIndex] > currentValue)
15 {
16 nums[preIndex + gap] = nums[preIndex];
17 preIndex -= gap;
18 }
19 //while循环结束时,说明已经找到了当前待排序的合适位置,插入
20 nums[preIndex + gap] = currentValue;
21 }
22 System.out.println("本轮增量【" + gap + "】排序后的数组");
23 gap /= 2;
24 }
25 return nums;
26}