排序 4快速排序
700 Words|Read in about 3 Min|本文总阅读量次
经典的排序算法,快速排序
0准备
1//建立一个排序用的顺序表结构L
2#define MAXSIZE 9
3typedef struct SqList
4{
5 int r[MAXSIZE];
6 int length;
7}SqList;
8/*排序的交换函数*/
9void swap(SqList* L,int i,int j)
10{
11 int temp = L->r[i];
12 L->r[i] = L->r[j];
13 L->r[j] = temp;
14}
1快速排序(Quicksort))
对冒泡排序的一种改进,也是采用分治法的一个典型的应用。
首先任意选取一个数据(比如数组的第一个数)作为关键数据,我们称为基准数,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序,也称为分区(partition)操作。
通过一趟快速排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
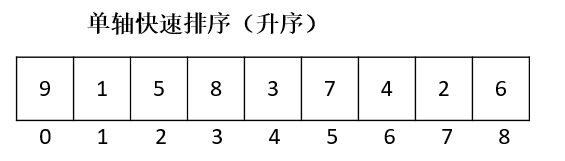
单枢轴的快速排序
1void QSort(SqList *L, int low, int high);
2int Partition(SqList *L, int low, int high);
3/*向外封装一个函数*/
4void QuickSort(SqList *L)
5{
6 QSort(L, 0, L->length - 1);
7}
8/*对顺序表工中的子序列L->r[1ow..high]作快速排序*/
9void QSort(SqList *L, int low, int high)
10{
11 int pivot;/*设置枢轴*/
12 if(low < high)
13 {
14 pivot = Partition(L, low, high);
15 QSort(L, low, pivot - 1);
16 QSort(L, pivot + 1, high);
17 }
18}
19/*使枢轴记录到位,并返回其所在位置*/
20int Partition(SqList *L, int low, int high)
21{
22 int pivotkey;
23 pivotkey = L->r[low];
24 while(low < high)
25 {
26 while(low < high && L->r[high] >= pivotkey)/*>=原则相等不交换*/
27 high--;
28 swap(L, low, high);
29 while(low < high && L->r[low] <= pivotkey)
30 low++;
31 swap(L, low, high);
32 }
33 return low;/*返回枢轴所在位置*/
34}
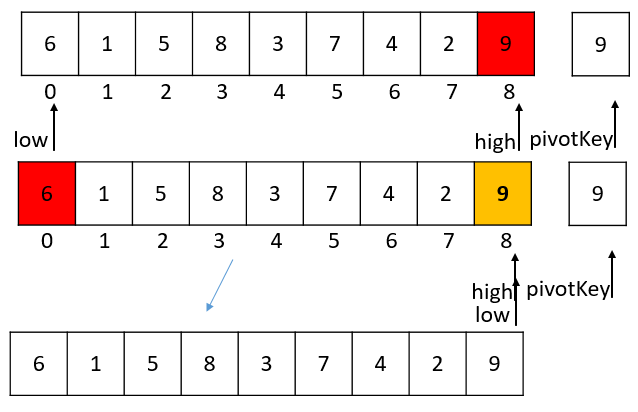
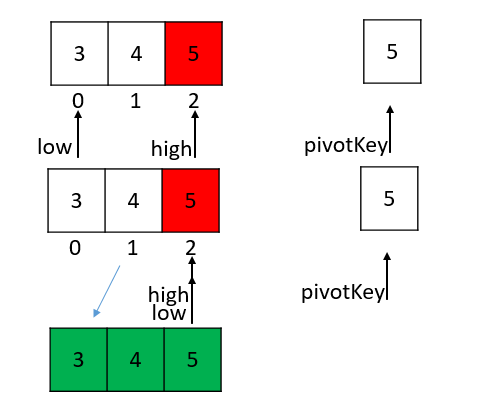
为了让图形更加直观,红色代表当前的外层循环的起始判断点,橘黄色代表的下标为最终返回的枢轴,绿色为已经排序完成的数组。
pivotKey = 9, pivot(low) = 8
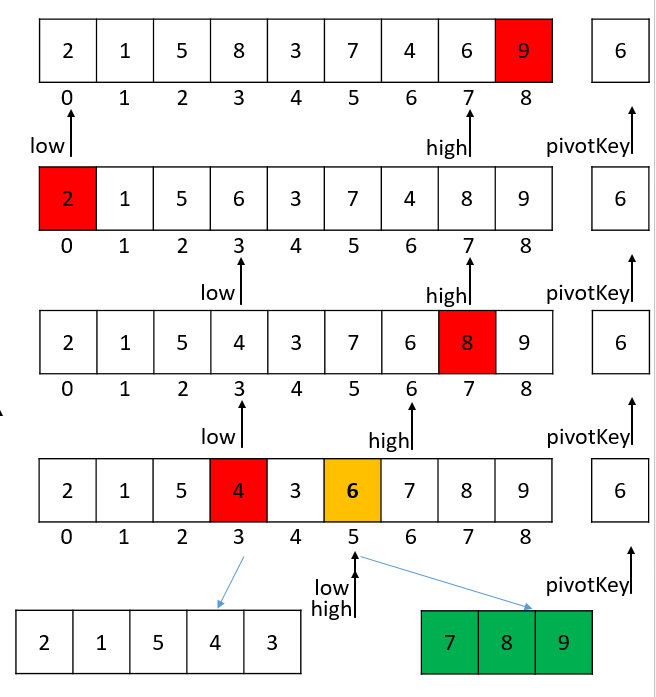
pivotKey = 6, pivot(low) = 5
pivotKey = 2, pivot(low) = 1
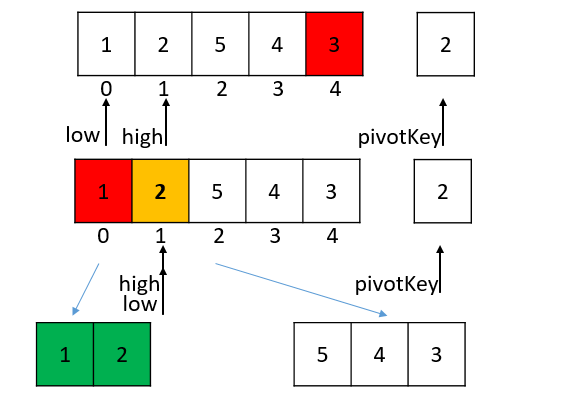
pivotKey = 5, pivot(low) = 2
Java版本的单枢轴排序
1//Java版本的单枢轴排序
2public int[] QuickSort(int[] nums)
3{
4 return sort(nums, 0, nums.length - 1);
5}
6
7public static int[] sort(int[] array, int start, int end)
8{
9 if(array.length < 1 || start < 0 || end >= array.length || start > end)
10 {
11 rentun null;
12 }
13 //数据分割成独立的两部分,从哪里分区的指示器
14 int zoneIndex = partition(array, start, end);
15 if(zoneIndex > start)
16 {
17 sort(array, start, zoneIndex - 1);
18 }
19 if(zoneIndex < end)
20 {
21 sort(array, zoneIndex + 1, end);
22 }
23 System.out.Println("本轮排序后的数组");
24 return array;
25}
26
27//快排分区方法
28public static int partition(int[] array, int start, int end)
29{
30 if(strat == end) return start;
31 //随机选取一个基准数
32 int pivot = (int)(start + Math.random() * (end - start + 1));
33 //zoneIndex是分区指示器,初始值为分区头元素下标减一
34 int zoneIndex = start - 1;
35 System.out.println("开始下标" + start + "结束下表" + end + "基准数下标" + pivot + "元素值" + array[pivot] + "分区指示器下标" + zoneIndex);
36 //将基准数和分区尾元素交换位置
37 swap(array, pivot, end);
38 for(int i = start; i <= end; i++)
39 {
40 //当前元素小于等于基准数
41 if(array[i] <= array[end]; i++)
42 {
43 //首先分区指示器累加
44 zoneIndex++;
45 //当前元素在分区指示器的右边时,交换当前元素和分区指示器元素
46 if(i > zoneIndex)
47 {
48 swap(array, i, zoneIndex);
49 }
50 }
51 System.out.Println("分区指示器" + zoneIndex);
52 }
53 return zoneIndex;
54}
55
56//交换数组内两个元素
57public static void swap(int[] array, int i, int j)
58{
59 int tmp = array[i];
60 array[i] = array[j];
61 array[j] = tmp;
62}
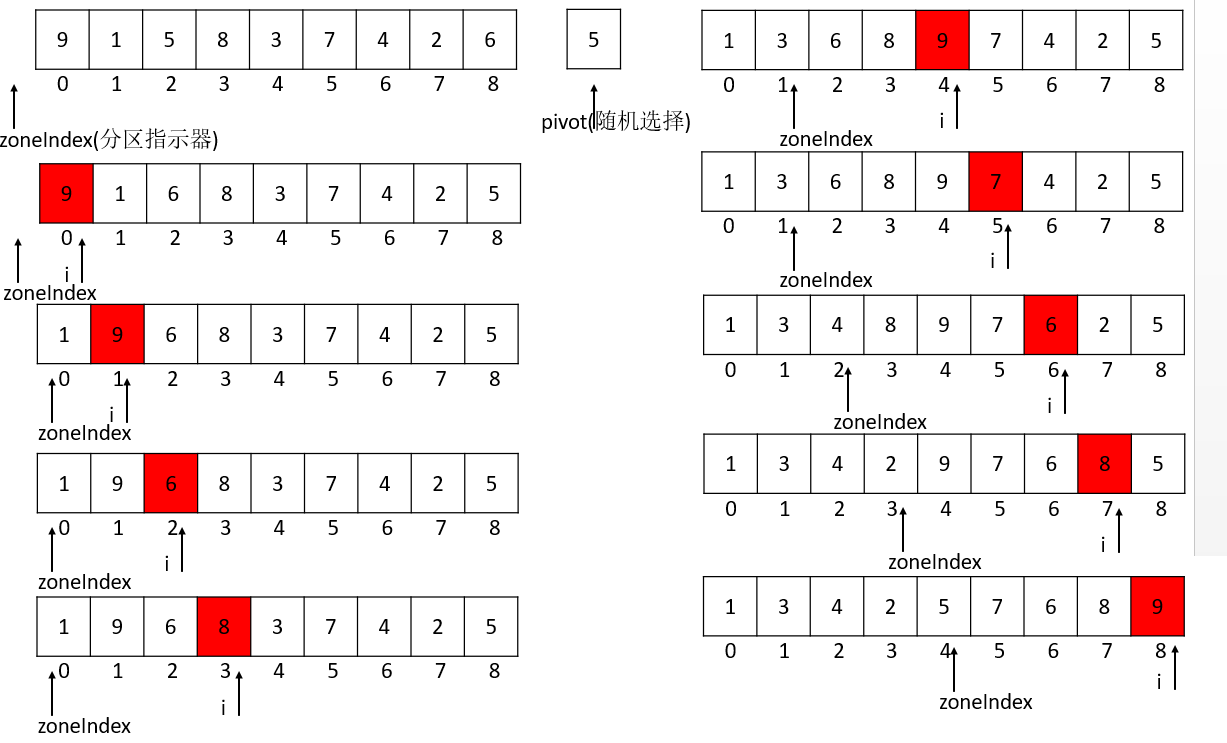
Java分类枢轴的方式,使用分区指示器,如下所示
分区指示器
- 如果当前元素小于等于基准数时,首先分割指示器右移一位:
- 在上面的基础之上,如果当前元素下标大于分割指示器下标时,当前元素和分割指示器所指元素交换。
基于双轴的快速排序
基于双轴的快速排序
双轴和单轴的区别你也可以知道,多一个轴,前面讲了快排很多时候选最左侧元素以这个元素为轴将数据划分为两个区域,递归分治的去进行排序。但单轴很多时候可能会遇到较差的情况就是当前元素可能是最大的或者最小的,这样子元素就没有被划分区间,快排的递推T(n)=T(n-1)+O(n)从而为O(n2).
双轴就是选取两个主元素理想将区间划为3部分,这样不仅每次能够确定元素个数增多为2个,划分的区间由原来的两个变成三个,最坏最坏的情况就是左右同大小并且都是最大或者最小,但这样的概率相比一个最大或者最小还是低很多很多,所以双轴快排的优化力度还是挺大的。
1//基于双轴的快速排序,基于JDK 1.8 Arrays.sort中的DualPivotQuicksort也是类似的方式
2import java.util.Arrays;
3
4public class DualPivotQuicksort {
5 public static void main(String[] args) {
6 int a[]= {7,3,5,4,8,5,6,55,4,333,44,7,885,23,6,44};
7 dualPivotQuickSort(a,0,a.length-1);
8 System.out.println(Arrays.toString(a));
9 }
10
11 private static void dualPivotQuickSort(int[] arr, int start, int end) {
12 if(start>end)return;//参数不对直接返回
13 if(arr[start]>arr[end])
14 swap(arr, start, end);
15 int pivot1=arr[start],pivot2=arr[end];//储存最左侧和最右侧的值
16 //(start,left]:左侧小于等于pivot1 [right,end)大于pivot2
17 int left=start,right=end,k=left+1;
18 while (k<right) {
19 //和左侧交换
20 if(arr[k]<pivot1)
21 {
22 //需要交换
23 swap(arr, ++left, k++);
24 }
25 else if (arr[k]<=pivot2) {//在中间的情况
26 k++;
27 }
28 else {
29 while (arr[right]>pivot2) {//如果全部小于直接跳出外层循环
30
31 if(right--==k)
32 break ;
33 }
34 if(k>=right)break ;
35 swap(arr, k, right);
36 }
37 }
38 swap(arr, start, left);
39 swap(arr, end, right);
40 dualPivotQuickSort(arr, start, left-1);
41 dualPivotQuickSort(arr, left+1, right-1);
42 dualPivotQuickSort(arr, right+1, end);
43 }
44 static void swap(int arr[],int i,int j)
45 {
46 int team=arr[i];
47 arr[i]=arr[j];
48 arr[j]=team;
49 }
50}
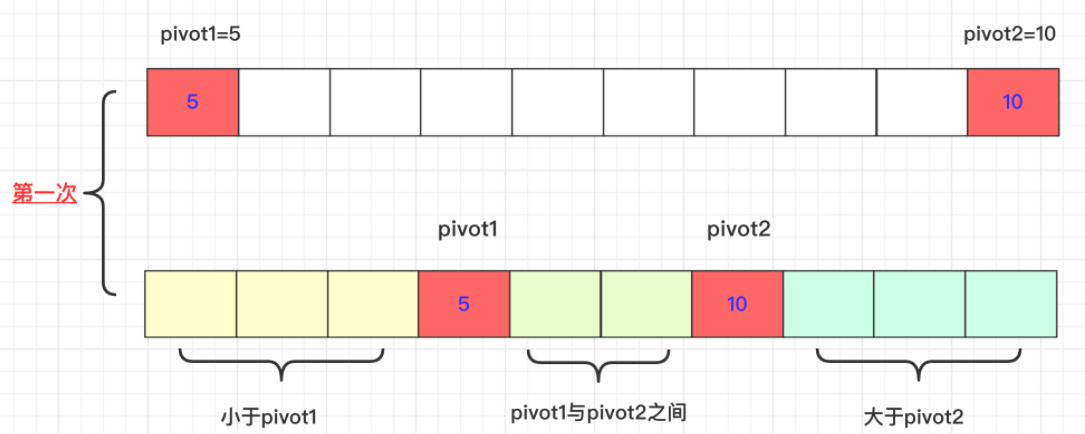
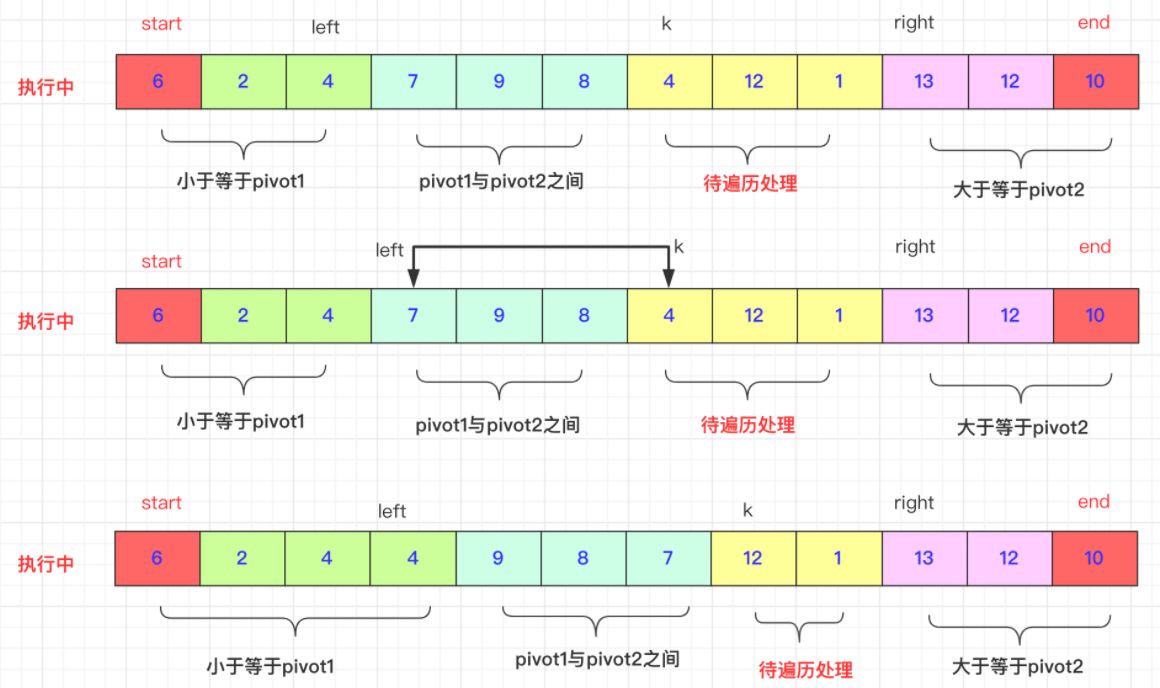
1)首先在初始的情况我们是选取待排序区间内最左侧、最右侧的两个数值作为pivot1和pivot2作为两个轴的存在。同时我们会提前处理数组最左侧和最右侧的数据会比较将最小的放在左侧。所以pivot1<pivot2.
而当前这一轮的最终目标是,比privot1小的在privot1左侧,比privot2大的在privot2右侧,在privot1和privot2之间的在中间。
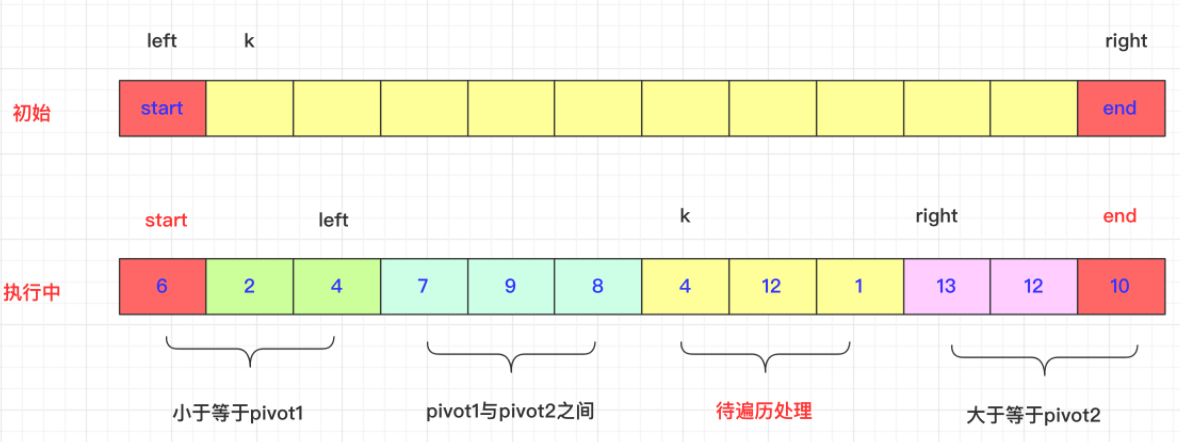
- 假设知道排序区间[start,end]。数组为ar,pivot1=arr[start],pivot2=arr[end]
- 还需要三个参数left,right和k。
- left初始为start,[stat,Ieft]区域即为小于等于pivot1小的区域(第一个等于)。
- right与left对应,初始为end,[right,end]为大于等于pivot2的区域(最后一个等于)。
- k初始为start+1,是一个从左往右遍历的指针,遍历的数值与pivot1,pivot2比较进行适当交换,当k>=right即可停止。
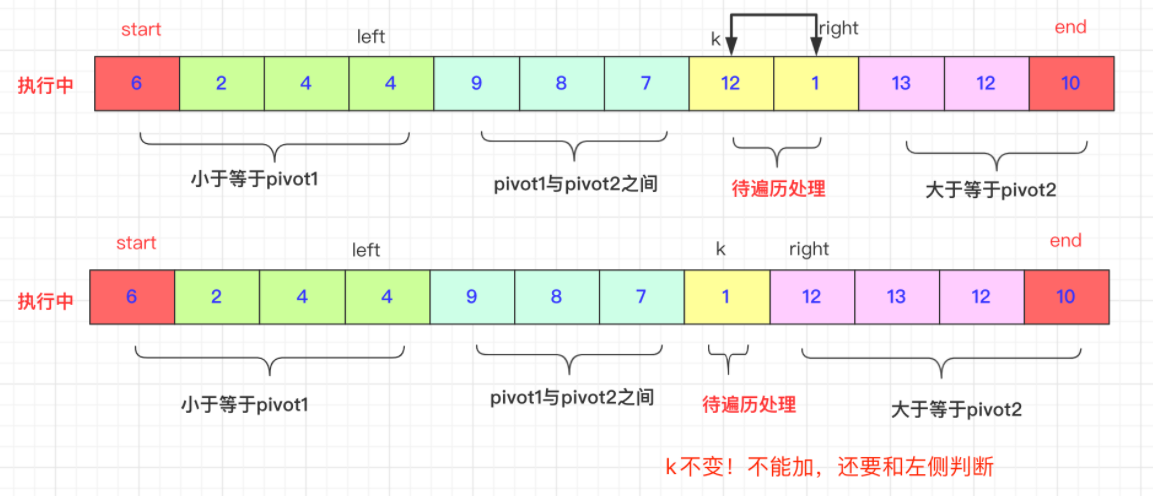
2)k交换过程 首先K是在lef和right中间的,遍历k的位置和pivot1,pivot2进行比较:
i)如果arr[k]<pivot1,那么先++left,然后swap(arr,k,left),因为初始在start在这个过程不结束start先不动。然后k++;继续进行
ii)而如果arr[k]>pivot2.(区间自行安排即可)有点区别的就是right可能连续的大于ar[k],比如93397如果我们需要跳过7前面9到3才能正常交换,这和快排的交换思想一致,当然再具体的实现上就是right–到一个合适比arr[k]小的位置。然后swap(arr,k,right)切记此时k不能自加。因为带交换的那个有可能比pivot1还小要和left交换。
iii)如果是介于两者之间,k++即可
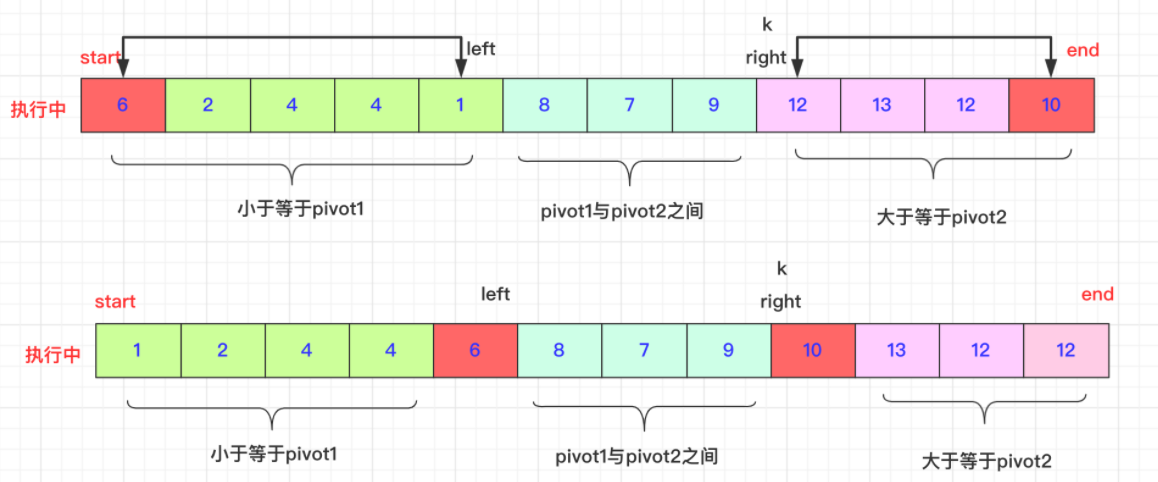
3)最后递归操作
在执行完这一趟即k=right之后,即开始需要将pivot1和pivot2的数值进行交换。然后三个区间根据编号递归执行排序函数即可。
1swap(arr, start, left);
2swap(arr, end, right);