经典的排序算法，插入排序

0准备

 1//建立一个排序用的顺序表结构L
 2#define MAXSIZE 9
 3typedef struct SqList
 4{
 5    int r[MAXSIZE];
 6    int length;
 7}SqList;
 8/*排序的交换函数*/
 9void swap(SqList* L,int i,int j)
10{
11    int temp = L->r[i];
12    L->r[i] = L->r[j];
13    L->r[j] = temp;
14}

1插入排序

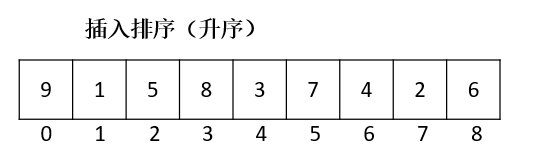
将一个记录插入到已经排好序的有序表中，从而得到一个新的、记录数增1的有序表。中心思想：设置额外空间，增加序列移动

  • 对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
  • 为了给要插入的元素腾出空间，我们需要将插入位置之后的已排序元素在都向右移动一位。插入排序所需的时间取决于输入中元素的初始顺序。例如，对一个很大且其中的元素已经有序【或接近有序)的数组进行排序将会比对随机顺序的数组或是逆序数组进行排序要快得多。

总的来说，插入排序对于部分有序的数组十分高效，也很适合小规模数组。

C的版本

 1void InsertSort(SqList *L)
 2{
 3    int i = 0, j = 0;
 4    for(i = 1; i < L->length; i++)
 5    {
 6         if(L->r[i] < L->r[i - 1])
 7         {
 8             int Sentry = L->r[i];/*设置哨兵*/
 9             for(j = i - 1; j >= 0; j--)/*>符号的原则，相等不交换*/
10             {
11                 if(L->r[j] > Sentry)
12                 {
13                     L->r[j + 1] = L->r[j];
14                 }
15             }
16             L->r[j + 1] = Sentry;
17         }
18    }
19}

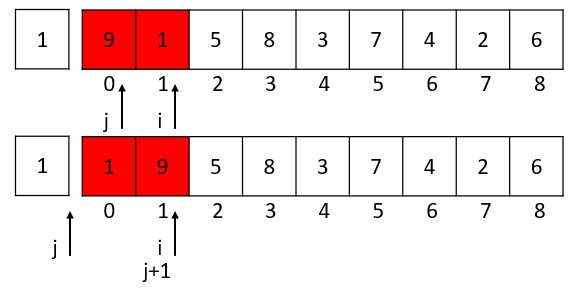
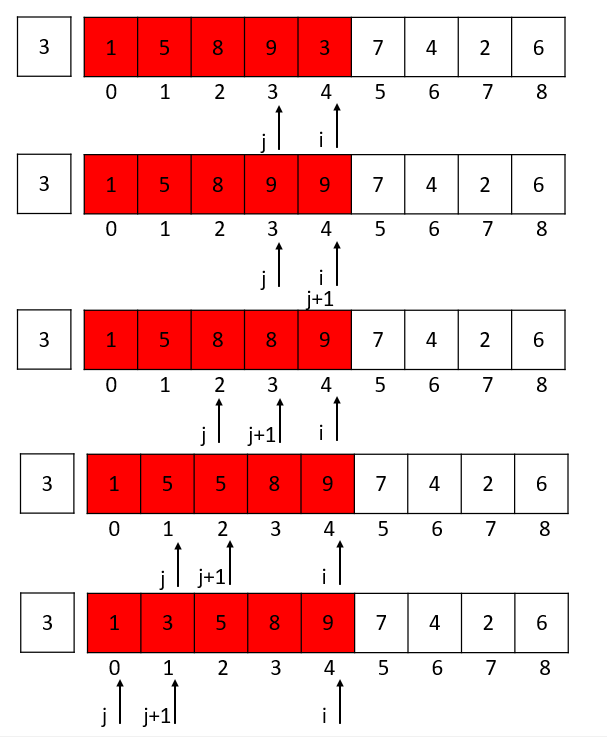
i = 1的时候

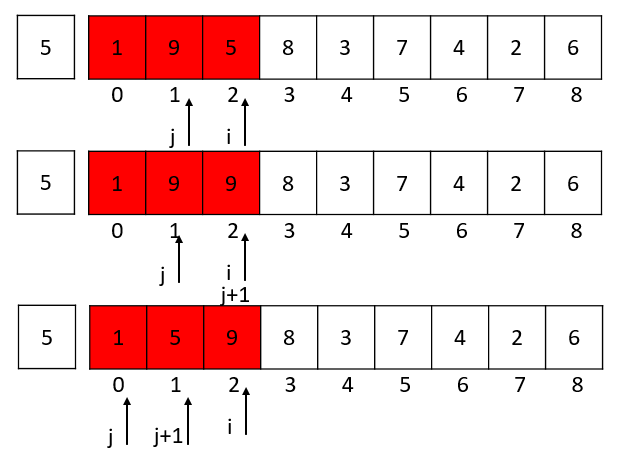
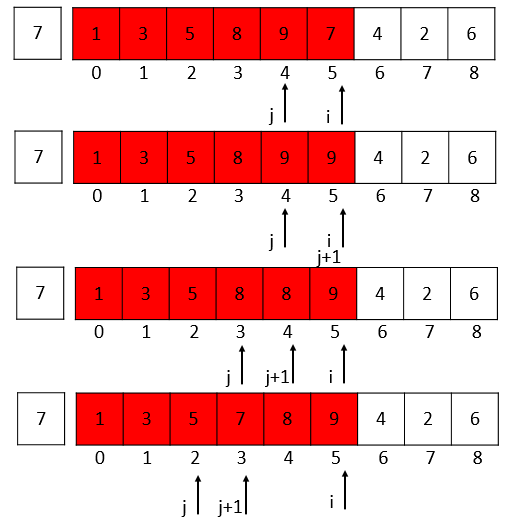
i = 2的时候

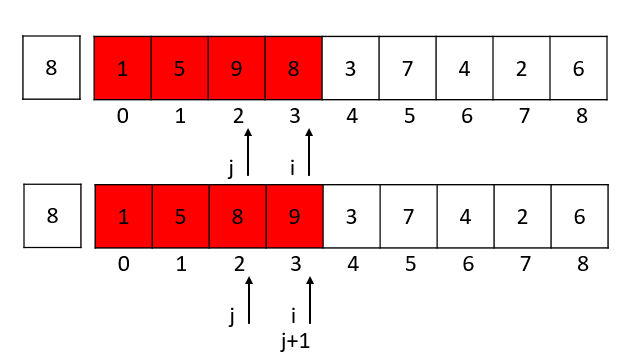
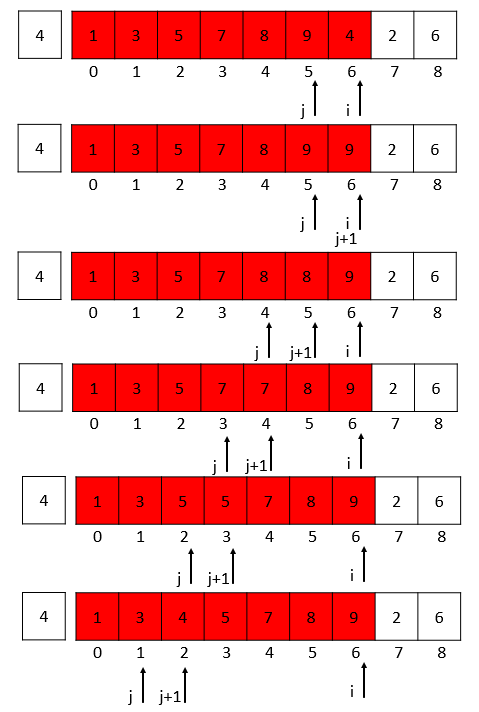
i = 3的时候

i = 4的时候

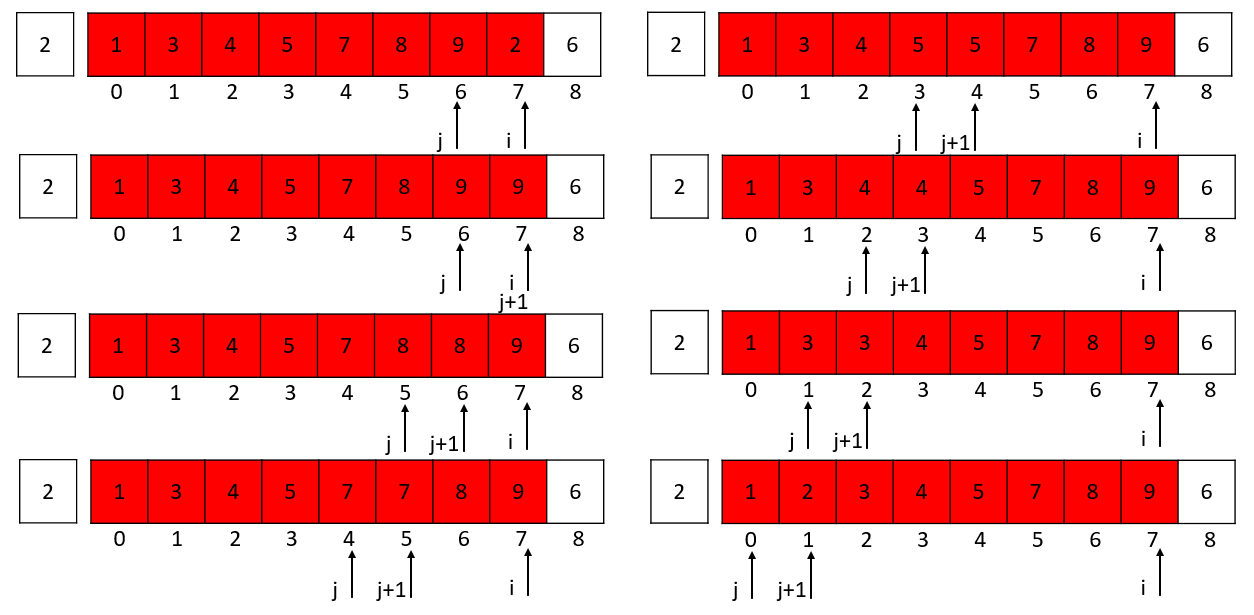
i = 5的时候

i = 6的时候

i = 7的时候

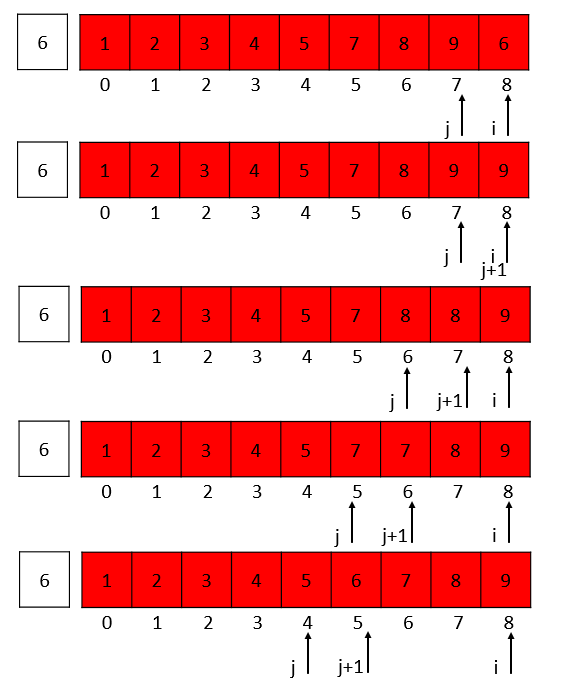
i = 8的时候

Java版本

 1public int[] InsertSort(int[] nums)
 2{
 3    if(nums.length == 0)
 4    {
 5        return nums;
 6    }
 7    int currentValue;//当前待排数据，该元素之前的元素均已被排序过
 8    for(int i = 0; i < nums.length; i++)
 9    {
10        int preIndex = i;
11        currentValue = nums[preIndex + 1];
12        System.out.Println("待排序元素索引" + (i + 1) + " ,值为:" + currentValue + " ,已被排序数据索引" + preIndex);
13        while(preIndex >= 0 && currentValue < nums[preIndex])
14        {
15            nums[preIndex + 1] = nums[preIndex];
16            preIndex--;
17        }
18        nums[preIndex + 1] = currentValue;
19        System.out.Println("本轮被插入数据");
20    }
21    return nums;
22}

除了上述的插入排序，还存在着成对插入排序

具体执行过程：上面的do-while循环已经排好的最前面的数据

  • 将要插入的数据，第一个值赋值a1,第二个值赋值a2,
  • 然后判断a1与a2的大小，使a1要大于a2
  • 接下来，首先是插入大的数值a1，将a1与k之前的数字一一比较，直到数值小于a1为止，把a1插入到合适的位置，注意：这里的相隔距离为2
  • 接下来，插入小的数值a2,将a2与此时k之前的数字一一比较，直到数值小于a2为止，将a2插入到合适的位置，注意：这里的相隔距离为1
  • 最后把最后一个没有遍历到的数据插入到合适位置
 1//成对插入排序
 2//JDK 1.8 Arrays.sort中的DualPivotQuicksort使用到了这种方式
 3DoublicInsetSort(int[] a, int left, int right)
 4{
 5    do {
 6        if (left >= right) {
 7            return;
 8        }
 9    } while (a[++left] >= a[left - 1]);
10
11    for (int k = left; ++left <= right; k = ++left) {
12        int a1 = a[k], a2 = a[left];
13
14        if (a1 < a2) {
15            a2 = a1; a1 = a[left];
16        }
17        while (a1 < a[--k]) {
18            a[k + 2] = a[k];
19        }
20        a[++k + 1] = a1;
21
22        while (a2 < a[--k]) {
23            a[k + 1] = a[k];
24        }
25        a[k + 1] = a2;
26    }
27    int last = a[right];
28
29    while (last < a[--right]) {
30        a[right + 1] = a[right];
31    }
32    a[right + 1] = last;
33}