排序 10基数排序
500 Words|Read in about 3 Min|本文总阅读量次
经典的排序算法,基数排序
0准备
1//建立一个排序用的顺序表结构L
2#define MAXSIZE 9
3typedef struct SqList
4{
5 int r[MAXSIZE];
6 int length;
7}SqList;
8/*排序的交换函数*/
9void swap(SqList* L,int i,int j)
10{
11 int temp = L->r[i];
12 L->r[i] = L->r[j];
13 L->r[j] = temp;
14}
基数排序(RadixSort)
基数是什么意思?
对于十进制整数,每一位都只可能是0~9中的某一个,总共10种可能。那10就是它的基,同理二进制数字的基为2;对于字符串,如果它使用的是8位的扩展ASC字符集,那么它的基就是256。
常见的数据元素一般是由若干位组成的,比如字符串由若干字符组成,整数由若干位0~9数字组成。基数排序按照从右往左的顺序,依次将每一位都当做一次关键字,然后按照该关键字对数组的元素入桶,每一轮入桶都基于上轮入桶的结果;完成所有位的入桶后,整个数组就达到有序状态。
比如对于数字2985,从右往左就是先以个位为关键字进行入桶,然后是十位、百位、千位总共需要四轮。基数排序也是一种无需比较的排序算法。
例子中是按照个位-十位-百位的顺序进行基数排序,此种方式是从最低位开始排序,所以被称为最低位优先法(简称“LSD法”)。
同样还可以按照百位-十位-各位的顺序进行排序,称为最高位优先法(简称“MSD法”)
C的版本
1int maxbit(SqList *L, int n) //辅助函数,求数据的最大位数
2{
3 int maxData = L->r[0]; // 最大数
4 /// 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。
5 for (int i = 1; i < n; ++i)
6 {
7 if (maxData < L->r[i])
8 maxData = L->r[i];
9 }
10 int d = 1;
11 int p = 10;
12 while (maxData >= p)
13 {
14 //p *= 10; // Maybe overflow
15 maxData /= 10;
16 ++d;
17 }
18 return d;
19}
20void RadixSort(SqList *L) //基数排序
21{
22 int n = L->length;
23 int d = maxbit(L, n);
24 int* tmp = new int[n];
25 int* count = new int[10]; //计数器
26 int i, j, k;
27 int radix = 1;
28 for (i = 1; i <= d; i++) //进行d次排序
29 {
30 //每次分配前清空计数器
31 for (j = 0; j < 10; j++)
32 count[j] = 0;
33 //统计每个桶中的记录数
34 for (j = 0; j < n; j++)
35 {
36 k = (L->r[j] / radix) % 10;
37 count[k]++;
38 }
39 //将tmp中的位置依次分配给每个桶,求前缀和
40 for (j = 1; j < 10; j++)
41 count[j] += count[j - 1];
42 //将所有桶中记录依次收集到tmp中
43 for (j = n - 1; j >= 0; j--)
44 {
45 k = (L->r[j] / radix) % 10;
46 tmp[count[k] - 1] = L->r[j];
47 count[k]--;
48 }
49 //将临时数组的内容复制到data中
50 for (j = 0; j < n; j++)
51 L->r[j] = tmp[j];
52 //位数加1
53 radix = radix * 10;
54 }
55 delete[]tmp;
56 delete[]count;
57}
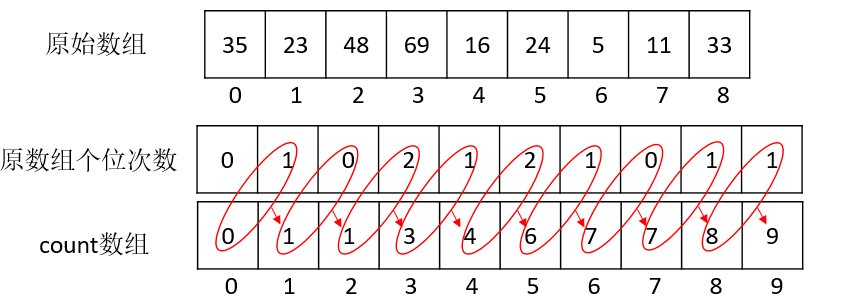
第一次个位数
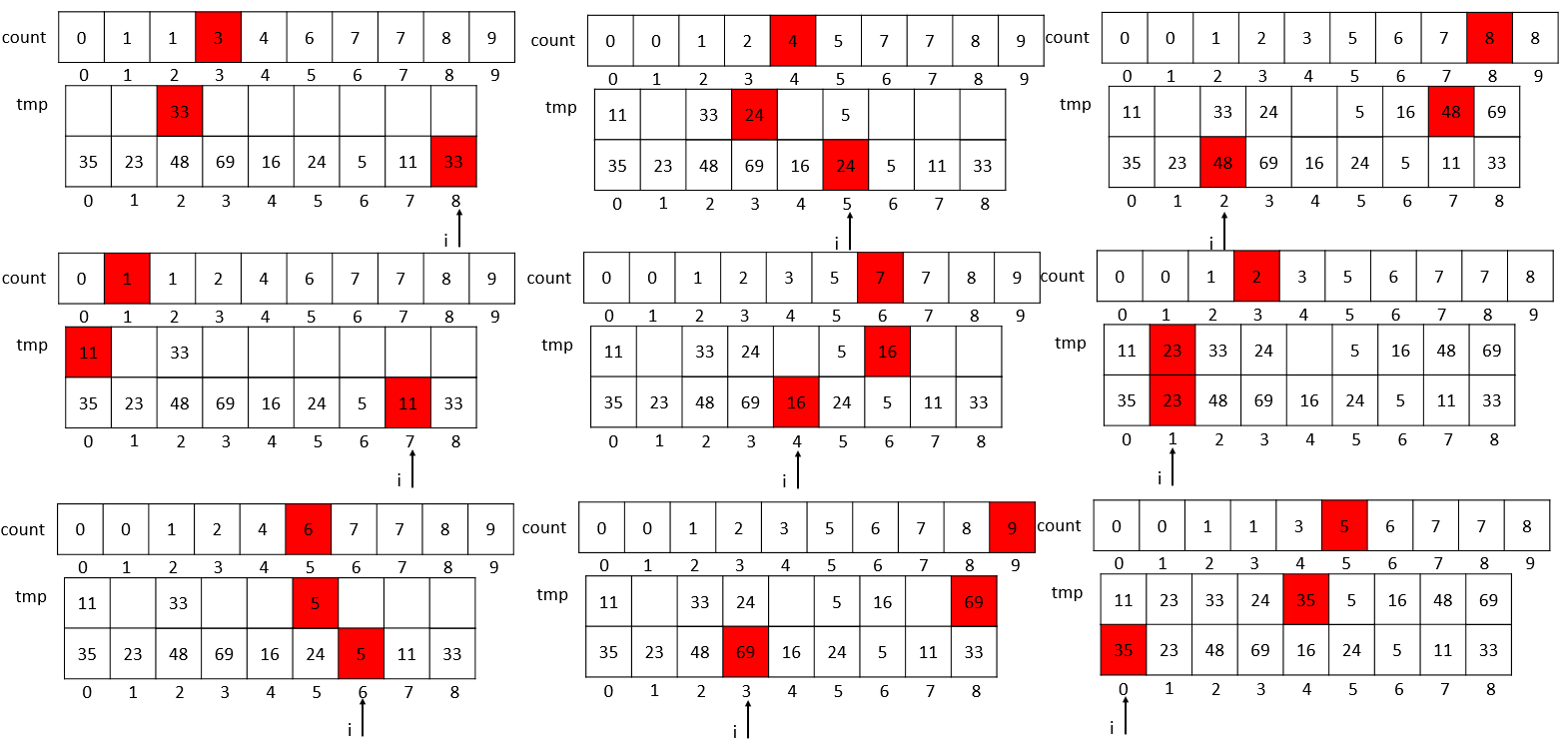
第一次过程
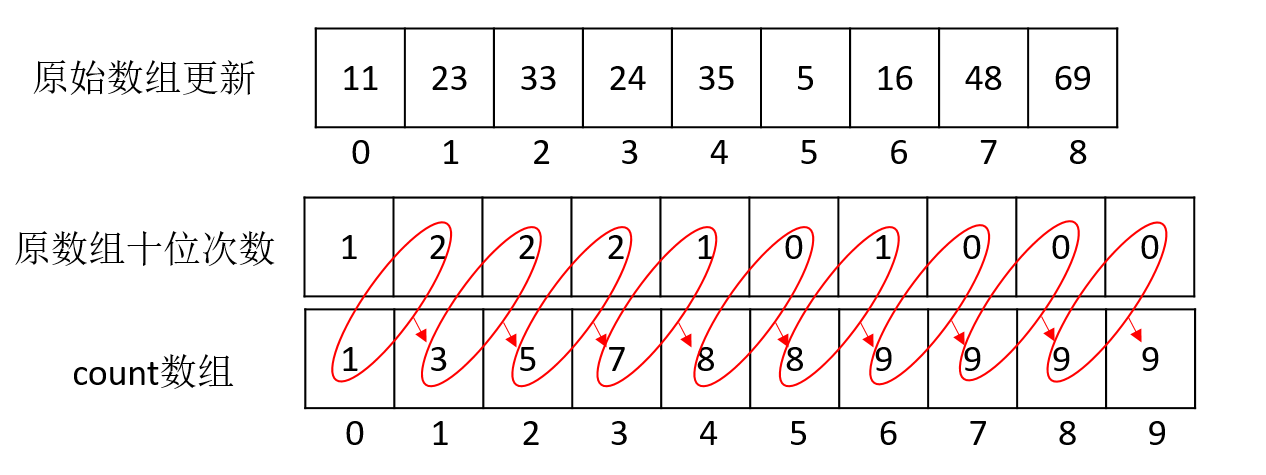
第二次十位数
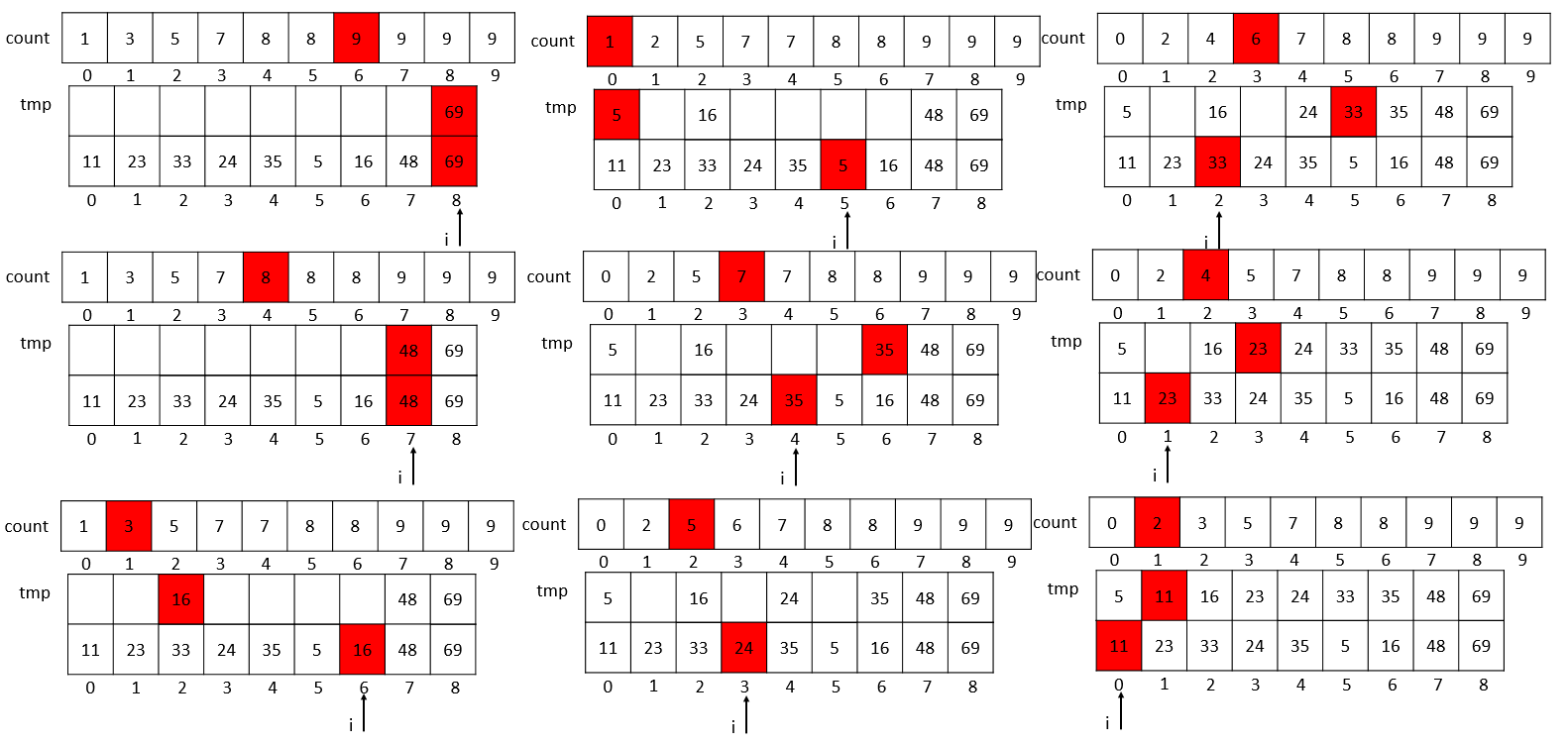
第二次过程
Java版本
1public int[] RadixSort(int[] nums)
2{
3 if(null == nums || nums.length < 2)
4 {
5 return nums;
6 }
7 //找出最大数
8 int max = nums[0];
9 for(int i = 0; i < nums.length; i++)
10 {
11 max = Math.max(max, nums[i]);
12 }
13 //先算出最大数的位数,他决定了我们需要进行几轮排序
14 int maxDigit = 0;
15 while(max != 0)
16 {
17 max /= 10;
18 maxDigit++;
19 }
20 int mod = 10, div = 1;
21 //构建桶
22 ArrayList<ArrayList<Integer>> bucketList = new ArrayList<ArrayList<Integer>>();
23 for(int i = 0; i < 10; i++)
24 {
25 bucketList.add(new ArrayList<Integer>());
26 }
27 //按照从右往左的顺序,一次将每一位都当做一次关键字,然后按照该关键字对数组排序,每一轮都基于上一轮排序的结果
28 for(int i = 0; i < nums.length; i++)
29 {
30 int num = (nums[j] % mod) / div;
31 bucketList.get(num).add(nums[j]);
32 }
33 //看看桶中数据的分布
34 for(int b = 0; b < bucketList.size(); b++)
35 {
36 System.out.println("第" + b + "个桶包含数据");
37 PrintArray.printObject(bucketList.get(b));
38 }
39 //桶中的数据回写原始数据,清楚桶,准备下一轮的排序
40 int index = 0;
41 for(int j = 0; j < bucketList.size(); j++)
42 {
43 for(int k = 0; k < bucketList.get(j).size(); k++)
44 {
45 nums[index++] = bucketList.get(j).get(k);
46 }
47 bucketList.get(j).clear();
48 }
49 return nums;
50}
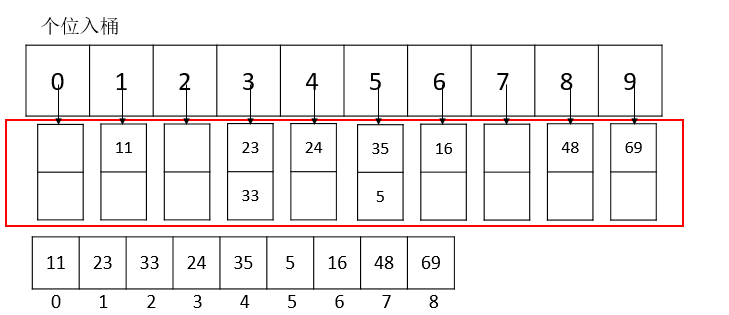
由于例子中是两位数,所以只需要考虑个位入桶和十位入桶即可
个位入桶
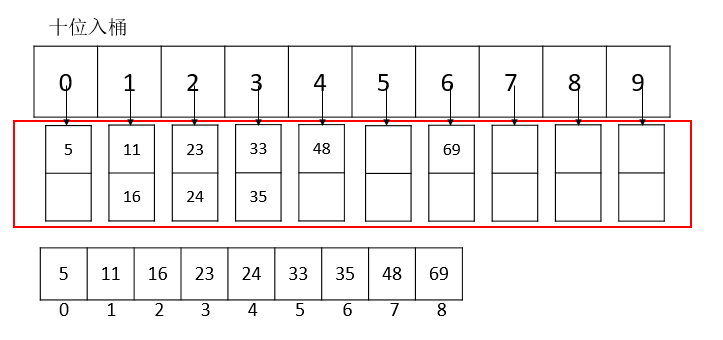
十位入桶
基数排序Vs计数排序Vs桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
- 基数排序:根据键值的每位数字来分配桶
- 计数排序:每个桶只存储单一键值
- 桶排序:每个桶存储一定范围的数值