经典的字符串匹配算法，BF(Brute Force)算法。

0准备

 1int main() {
 2    string s = "abababc";
 3    string p = "abc";
 4    string s1 = "abcdefgabcdee";
 5    string p1 = "abcdex";
 6    string s2 = "00000000000000000000000000000001";
 7    string p2 = "00000001";
 8    cout << BF(s, p) << endl;
 9    cout << BF(s1, p1) << endl;
10    cout << BF(s2, p2) << endl;
11}

BF(Brute Force)算法

BF(Brute Force)算法

又叫暴力匹配算法或者朴素匹配算法

思路很简单：在主串中取前下标为[0,m-1]这m个字符的子串和模式串逐个字符逐个字符比较，如果完全一样就结束并返回下标；如果有不一样的，那么主串中的子串后移一位，主串中[1,m]这个子串和模式串继续比较，… ，主串中[n-m,n-1]这个子串和模式串继续比较。主串中长度为m的子串有n-m+1个。

C的版本

 1int BF(string& s, string& pattern)
 2{
 3    int n = s.length(), m = pattern.length();
 4    for (int i = 0; i < n - m + 1; i++)
 5    {
 6        int j = 0;
 7        for (; j < m; j++)
 8        {
 9            if (i + j >= n || s[i + j] != pattern[j])
10                break;
11        }
12        if(j == m)
13        {
14            //匹配到了，返回主串中的下标
15            return i;
16        }
17    }
18    //匹配不到
19    return -1;
20}

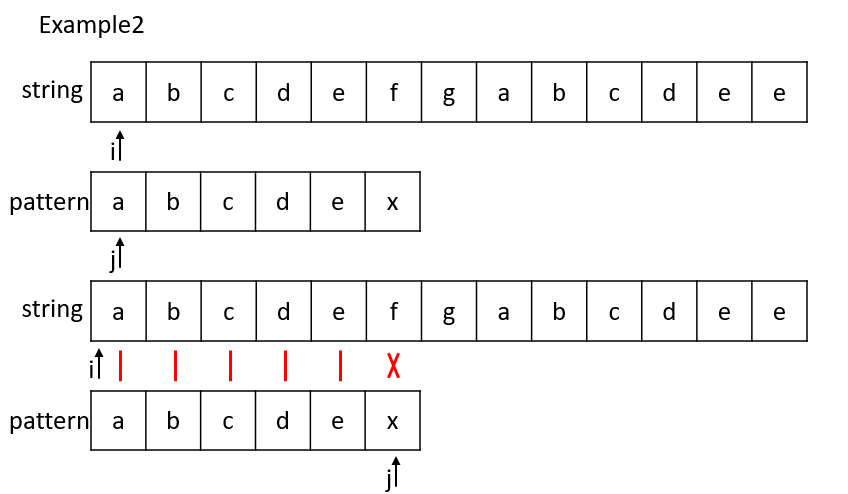
举例2，字符串"abcdedgabcdee"中匹配字符串"abcdex"。在i = 0会做一个匹配，但是最后一个字符匹配不上，只能继续遍历，在i = 7的时候会再一次匹配，但是最后一个字符匹配不上，最终返回-1。

i = 0

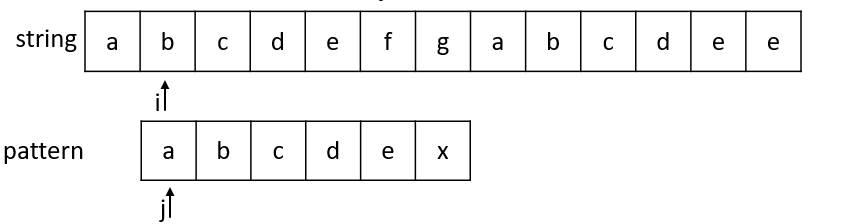
i = 1

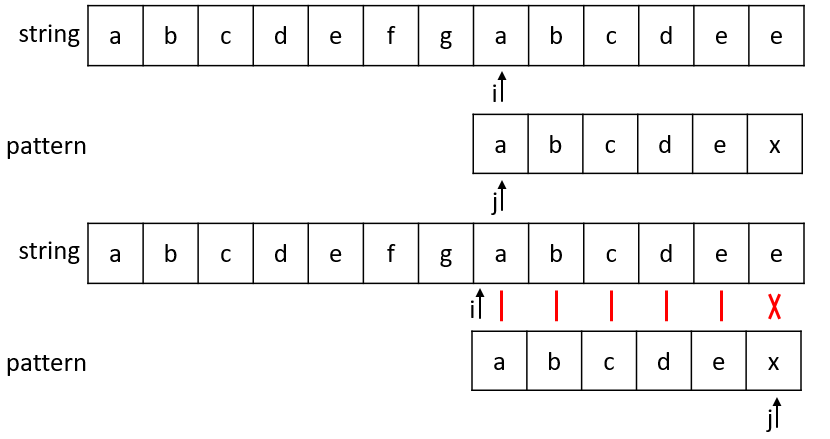
i = 7

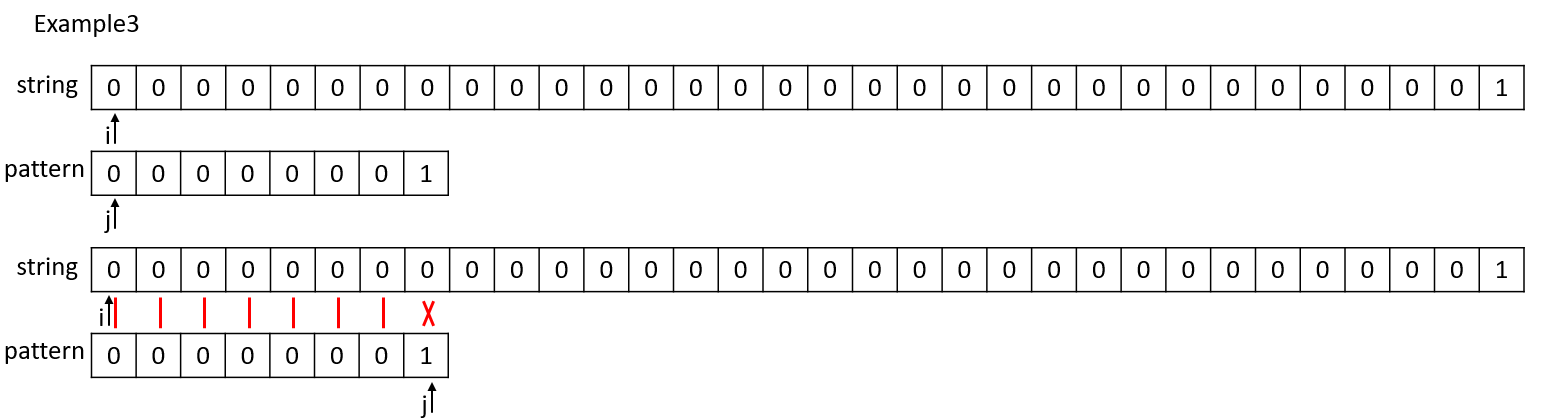
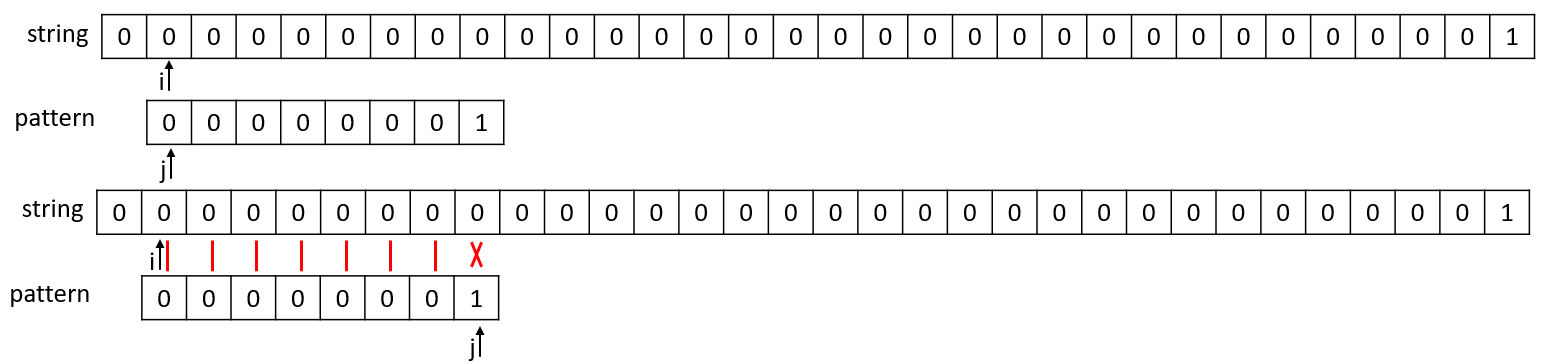
举例3可以发现，当32位的uint32型数值的字符串中匹配uint8型数值的字符串就会比较繁琐，从i = 0开始，直到i = 24位置才能够完全匹配，这就是BF的暴力求解法。

i = 0

i = 1

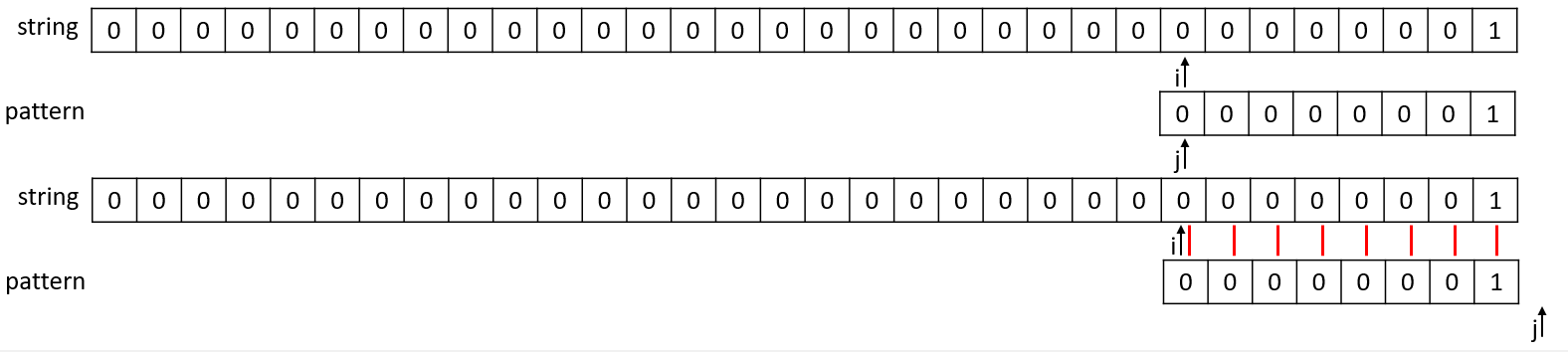
i = 24

Java版本

 1//String.java#indexOf
 2//jdk源码
 3static int indexOf(char[] source, int sourceOffset, int sourceCount,
 4                   char[] target, int targetOffset, int targetCount,
 5                   int fromIndex) {
 6    if (fromIndex >= sourceCount) {
 7        return (targetCount == 0 ? sourceCount : -1);
 8    }
 9    if (fromIndex < 0) {
10        fromIndex = 0;
11    }
12    if (targetCount == 0) {
13        return fromIndex;
14    }
15
16    char first = target[targetOffset];
17    int max = sourceOffset + (sourceCount - targetCount);
18
19    for (int i = sourceOffset + fromIndex; i <= max; i++) {
20        /* Look for first character. */
21        if (source[i] != first) {
22            while (++i <= max && source[i] != first);
23        }
24
25        /* Found first character, now look at the rest of v2 */
26        if (i <= max) {
27            int j = i + 1;
28            int end = j + targetCount - 1;
29            for (int k = targetOffset + 1; j < end && source[j]
30                 == target[k]; j++, k++);
31
32            if (j == end) {
33                /* Found whole string. */
34                return i - sourceOffset;
35            }
36        }
37    }
38    return -1;
39}

BF算法总结

最坏的情况下，在第一个for循环里，i 从0到n-m走满共n-m+1次，第二个for循环里，j 从0到m-1走满共m次，因此最坏的情况下时间复杂度为O(n*m)，上述例子中string a2 = "00000000000000000000000000000001"，string p2 = "00000001";所有n-m+1个子串都要走完，并且每次和模式串比较都要比较m次，总共比较n-m+1次，最坏的时间复杂度为o((n - m + 1) * m)

BF算法最大的优点就是简单，代码不容易出错，在主串和模式串的长度都不大的时候还是比较实用的。