动态规划
1100 Words|Read in about 5 Min|本文总阅读量次
数据结构中的动态规划,一起学习一下。
动态规划
从游戏中学习动态规划
Example1
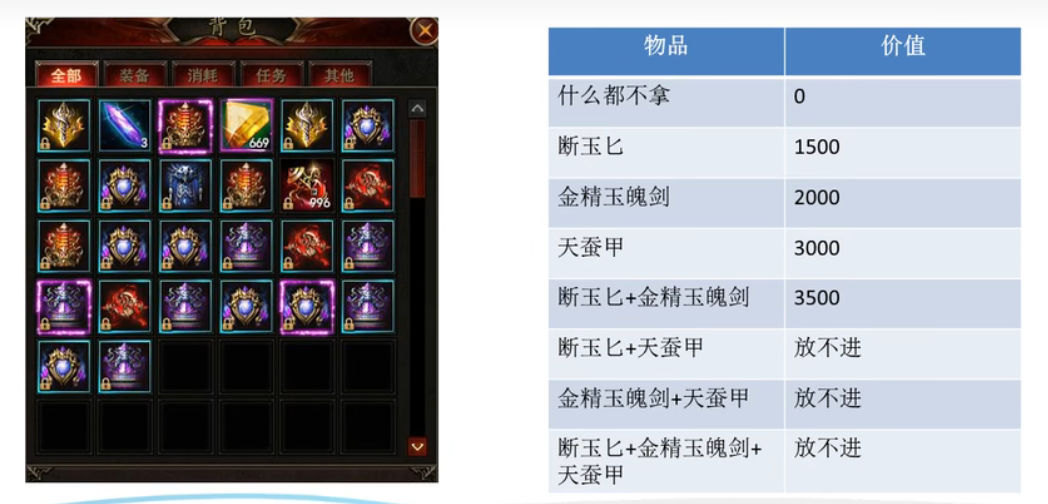
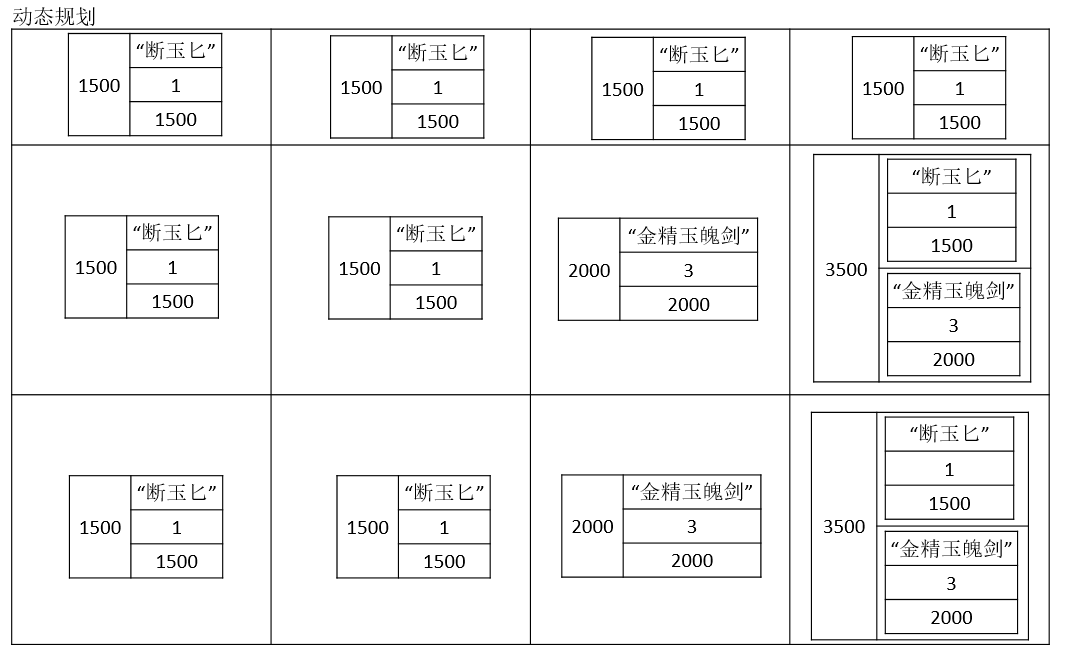
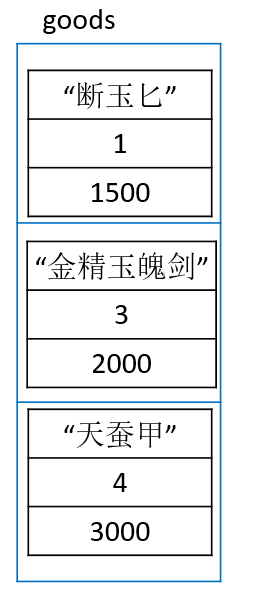
你有背包,有四个格子,下面有几样掉落的物品,你可以选择性的放进背包里面,然后将被宝贝送到游戏迷宫之后的NPC手中,NPC会将你背包中的物品折换成银两,你怎么操作可以使自己获取最大的收益。
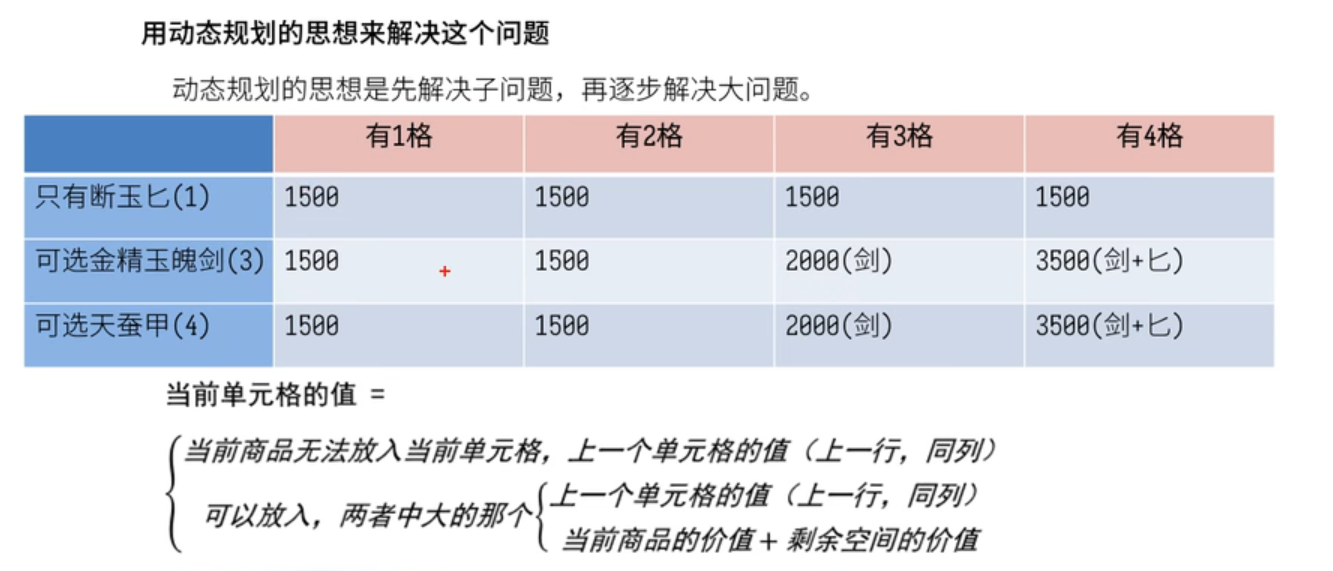
通常来说,可以用暴力求解的方式。把所有的可能性都罗列出来,然后得到结果,选取其中最大值即可。从时间复杂度来看是o(2^n^)
动态规划思想:先解决子问题,再来解决子问题组成的大问题
最终通过DP表格的形式,可以得到最大值3500(剑+匕)
Example2
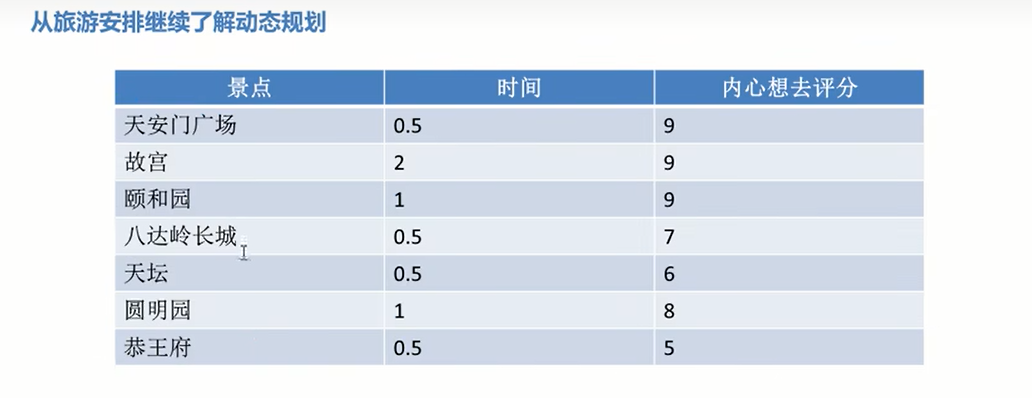
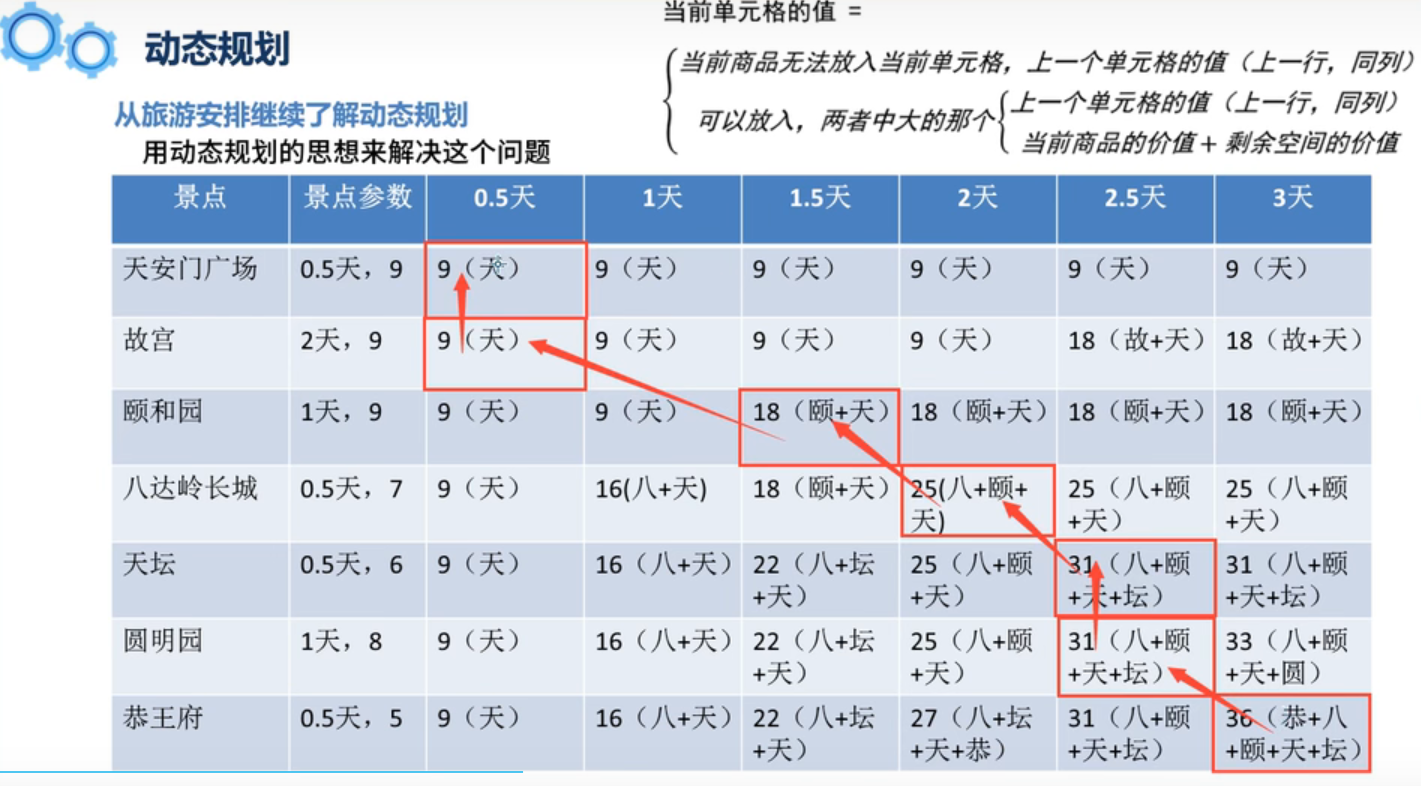
上面的例子物品比较少,可选择的点也比较少,这里列举一个去北京旅行的一个景点选择问题。
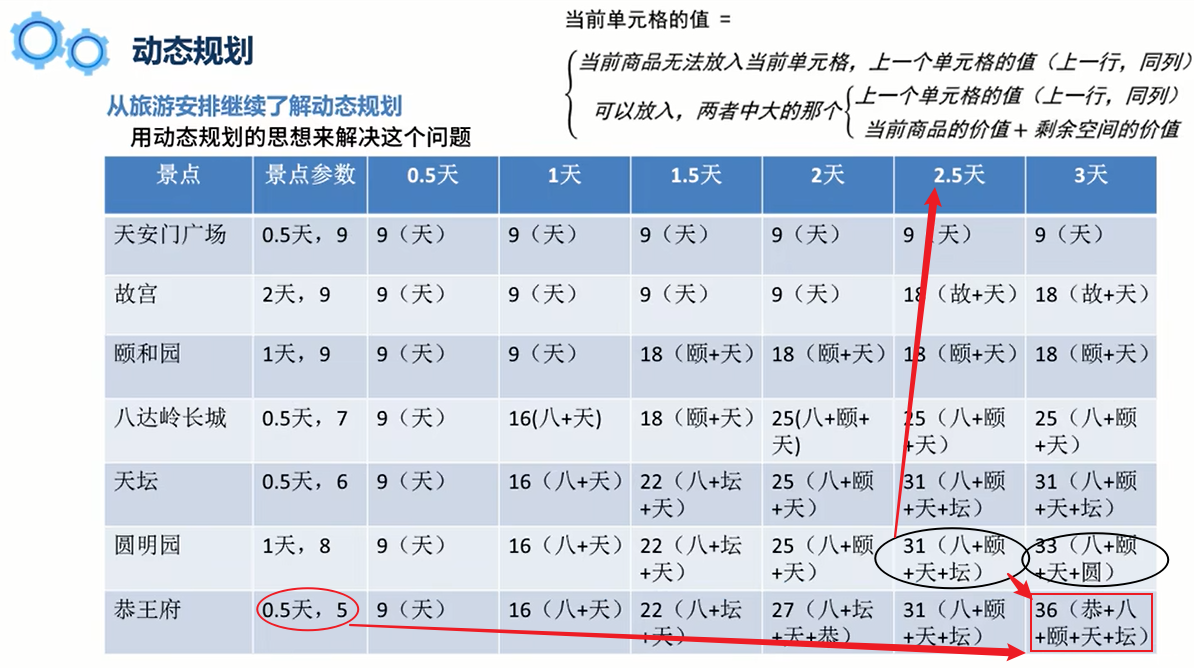
可以按照Example1得到类似的表格,其中以最后一个空格为例,已知2.5天的最大价值是31的评分,在没有恭王府之前3天的最大价值是33的评分,恭王府是0.5天,那么剩余的恭王府的评分5加上已经2.5天的最大值评分得到,36。这个评分大于没有恭王府之前3天的最大价值,所以填入36这个值。
因此Example2可以得到的最佳景点是(天安门+天坛+颐和园+八达岭长城+恭王府)
二维数组实现背包问题
1private static class ArrayElement{
2 //计算后的数组元素值
3 private int value;
4 //哪些物品的值组成了当前数组元素
5 private Set<Element> elements;
6 //加入单个元素
7 public ArrayElement(int value, Element element)
8 {
9 this.value = value;
10 this.elements = new HashSet<>();
11 this.elements.add(element);
12 }
13 //加入元素组
14 public ArrayElement(int value, Set<Element> elements)
15 {
16 this.value = value;
17 this.elements = elements;
18 }
19
20 @Override
21 public String toString()
22 {
23 return "BagElement{" +
24 "value = " + value +
25 ", elements = " + elements +
26 "}";
27 }
28}
29//放入背包的物品
30private static class Element{
31 private final String name;
32 //物品的价值
33 private final int value;
34 //物品的花费
35 private final int cost;
36
37 public Element(String name, int cost, int value)
38 {
39 this.name = name;
40 this.cost = cost;
41 this.value = value;
42 }
43
44 @Override
45 public String toString()
46 {
47 return "Element{" +
48 "name = " + name + '\' +
49 ", value = " + value +
50 ", cost = " + cost +
51 "}";
52 }
53}
54
55public void printArray(Element[] goods, int bagSize, ArrayElement[][] calc)
56{
57 for(int i = 0; i < goods.length; i++)
58 {
59 for(int j = 0; j < bagSize; j++)
60 {
61 System.out.println("i = " + i + " ,j = " + j + " ,calc = " + calc[i][j] + " ");
62 }
63 }
64}
65
66public void printRow(int rowNo, int bagSize, ArrayElement[][] calc)
67{
68 System.out.println("当前行号:" + rowNo);
69 for(int j = 0; j < bagSize; j++)
70 {
71 if(calc[rowNo][j] != null)
72 {
73 System.out.println("j = " + j + " ,calc = "+ calc[rowNo][j] + " ");
74 }
75 }
76}
77
78public void putBag(Element[] goods, int bagSize)
79{
80 ArrayElement[][] calcArray = new ArrayElement[goods.length][bagSize];
81 for(int i = 0; i < goods.length; i++)
82 {
83 for(int j = 0; j < bagSize; j++)
84 {
85 //第一行数据特殊处理
86 if(0 == i)
87 {
88 calcArray[i][j] = new ArrayElement(goods[i].value, goods[i]);
89 }else
90 {
91 //计算本单元格是否能够放下当前物品
92 int spareSpace = j + 1 - goods[i].cost;
93 //放不下,使用上一行同列的数据
94 if(spareSpace < 0)
95 {
96 calcArray[i][j] = calcArray[i - 1][j];
97 }else
98 {
99 //可以放下,需要判断上一行同列的值和当前商品的价值+剩余空间的价值哪个更大
100 //上一行同列的值
101 int preRowVlaue = calcArray[preRow][j].value;
102 //当前商品的价值
103 int currentGoodsValue = goods[i].value;
104 //是否有剩余空间,如果有,获取剩余空间最大价值
105 if(spareSpace > 0)
106 {
107 currentGoodsValue += calcArray[i - 1][spareSpace - 1].value;
108 }
109 if(preRowVlaue >= currentGoodsValue)
110 {
111 //使用上一行同列的数据
112 calcArray[i][j] = calcArray[i - 1][j];
113 }else
114 {
115 if(0 == spareSpace)
116 {
117 //空间只够存放当前物品
118 calcArray[i][j] = new ArrayElement(currentGoodsValue, goods[i]);
119 }else
120 {
121 //把商品叠加起来calcArray[i - 1][spareSpace - 1].elements含义是
122 //放置当前的goods[i]之后的剩余空间最大的价值
123 Set<Element> newElement = (HashSet<Element>)((HashSet<Element>)calcArray[i - 1][spareSpace - 1].elements);
124 newElement.add(goods[i]);
125 calcArray[i][j] = new ArrayElement(currentGoodsValue, newElement);
126 }
127 }
128 }
129 }
130 }
131 }
132}
133
134public static void main(String[] args)
135{
136 Element[] gameElements = {new Element("断玉匕", 1, 1500),
137 new Element("金精玉魄剑", 3, 2000),
138 new Element("天蚕甲", 1, 3000)};
139 Element[] tourElements = {new Element("天安门广场", 1, 9),
140 new Element("故宫", 4, 9),
141 new Element("八达岭长城", 1, 7),
142 new Element("天坛", 1, 6),
143 new Element("圆明园", 2, 8),
144 new Element("恭王府", 1, 5)};
145 putBag(tourElements, 6);
146}
代码实现如下
DP表
goods表
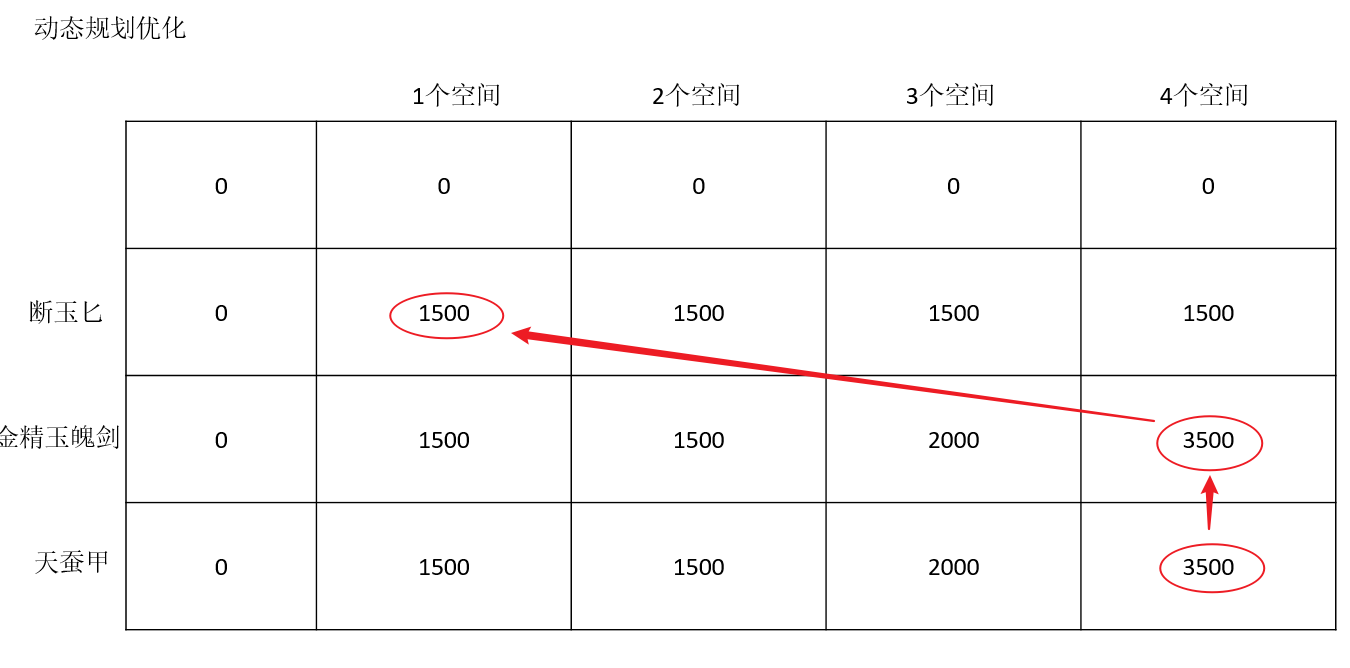
对于二位数组进一步优化,可以只留下value,不需要elements元素组,因为可以通过value值反推出当前value所包含的element,可以看到对应的红色标识指出的路线即为最大value的路线。
二维数组实现背包问题优化
1private static class Element
2{
3 private final String name;
4 private final int value;
5 private final int cost;
6
7 public Element(String name, int cost, int value)
8 {
9 this.name = name;
10 this.cost = cost;
11 this.value = value;
12 }
13}
14
15public void printArray(Element[] goods, int bagSize, ArrayElement[][] calc)
16{
17 for(int i = 0; i < goods.length; i++)
18 {
19 for(int j = 0; j < bagSize; j++)
20 {
21 System.out.println("i = " + i + " ,j = " + j + " ,calc = " + calc[i][j] + " ");
22 }
23 }
24}
25
26public void printRow(int rowNo, int bagSize, ArrayElement[][] calc)
27{
28 System.out.println("当前行号:" + rowNo);
29 for(int j = 0; j < bagSize; j++)
30 {
31 if(calc[rowNo][j] != null)
32 {
33 System.out.println("j = " + j + " ,calc = "+ calc[rowNo][j] + " ");
34 }
35 }
36}
37
38public void putBag(Element[] goods, int bagSize)
39{
40 int arrayX = goods.length + 1;
41 int arrayY = bagSize + 1;
42 int[][] calcArray = new int[arrayX][arrayY];
43 for(int i = 0; i < arrayX; i++)
44 {
45 for(int j = 0; j < arrayY; j++)
46 {
47 //第0行第0列赋值为0
48 if(0 == i || 0 == j)
49 {
50 calcArray[i][j] = 0;
51 }else
52 {
53 //当前物品在物品数组中的下标
54 int goodsIndex = i - 1;
55 int preRowValue = calcArray[i - 1][j];
56 //计算本单元格是否能放下当前物品
57 int spareSpace = j - goods[goodsIndex].cost;
58 //放不下,直接上用上一行同列的数据
59 if(spareSpace < 0)
60 {
61 calcArray[i][j] = preRowValue;
62 }else
63 {
64 //可以放下,需要判断sum1和sum2的值
65 //sum1:上一行同列的值
66 //sum2:当前商品价值+剩余空间的价值哪个更大
67 int currentGoodsValue = goods[goodsIndex].value;
68 if(spareSpace >= 0)
69 {
70 currentGoodsValue += calcArray[n - 1][spareSpace];
71 }
72 calcArray[i][j] = Math.max(preRowValue, currentGoodsValue);
73 }
74 }
75 }
76 }
77}
78
79public static void main(String[] args)
80{
81 Element[] gameElements = {new Element("断玉匕", 1, 1500),
82 new Element("金精玉魄剑", 3, 2000),
83 new Element("天蚕甲", 1, 3000)};
84 Element[] tourElements = {new Element("天安门广场", 1, 9),
85 new Element("故宫", 4, 9),
86 new Element("八达岭长城", 1, 7),
87 new Element("天坛", 1, 6),
88 new Element("圆明园", 2, 8),
89 new Element("恭王府", 1, 5)};
90 putBag(tourElements, 6);
91}
优化后代码实现如下
DP表
一维数组实现动态规划
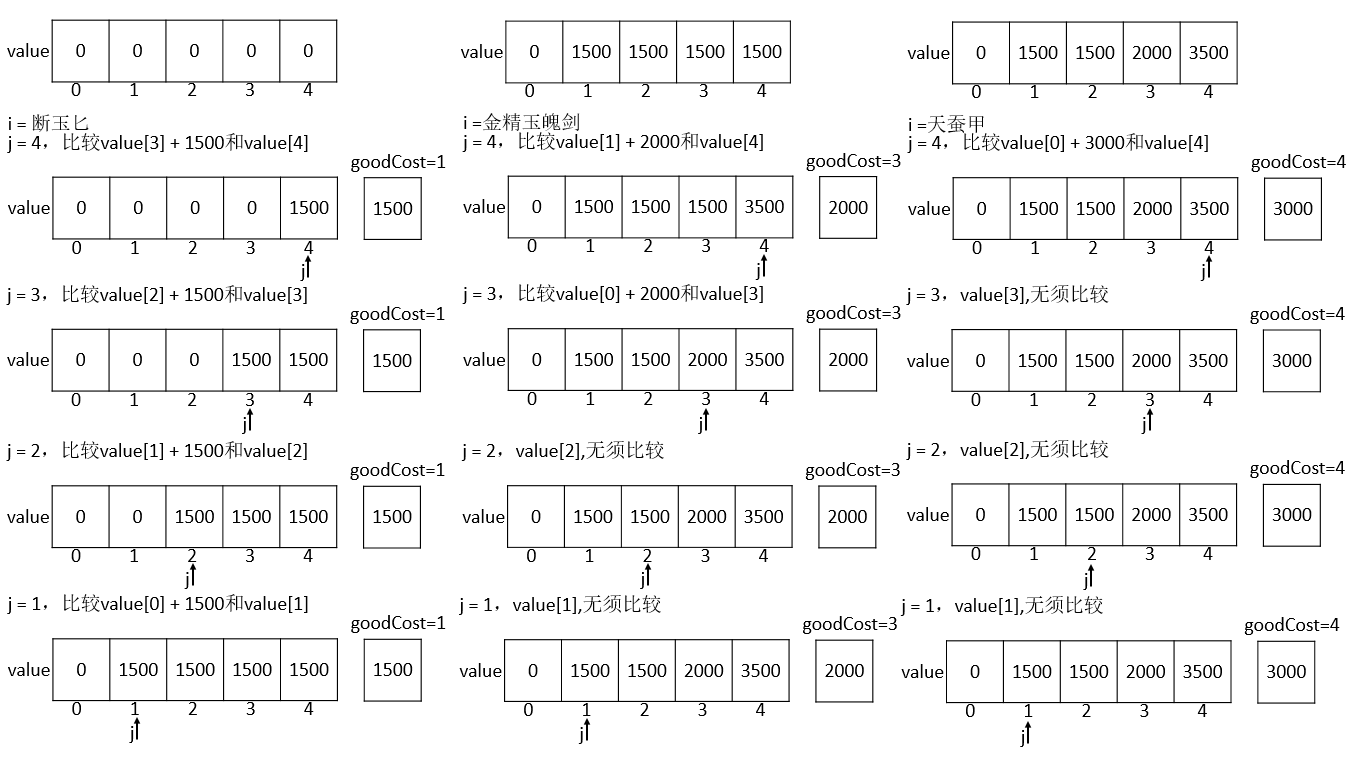
由于上面的二维数组中只是用到了部分的元素,剩余大部分空间都是浪费,其实转变为一种思想可以用一维数组来实现动态规划会更加节省空间。
1public void putBag(Element[] goods, int bagSize)
2{
3 int[] calcArray = new int[bagSize + 1];
4 calcArray[0] = 0;
5 for(int goodsIndex = 0; goodsIndex < goods.length; goodsIndex++)
6 {
7 int goodCose = goods[goodsIndex].cost;
8 System.out.println(goods[goodsIndex].name + ":空间耗费: " + goodsCost + " ,价值:" + goods[goodsIndex].value);
9 for(int currentSize = bagSize; currentSize > 0; currentSize--)
10 {
11 System.out.println("目前背包大小" + currentSize);
12 if(currentSize >= goodCost)
13 {
14 calcArray[currentSize] =
15 Math.max(calcArray[currentSize],
16 calcArray[currentSize - goodCost] + goods[goodsIndex].value);
17 }
18 }
19 }
20}
一维数组的遍历如下图所示
一维数组和二维数组对比
- 一维数组相对来说空间更加省略,需要倒序遍历来访问这个一维数组。一般求解一维数组只需要获取到最优值即可,因为无法获取最优值的相关回溯。
- 二维数组对比一维数组会提供更加多的细节,可以明确的了解到每个值最优解的回溯,但是由于存储了很多元素不是每一个都会用到,所以相对来说会存在数组冗余的现象。
动态规划
动态规划的定义
动态规划(Dynamic Programming,简称DP)是运筹学的一个分支,是求解决策过程最优化的过程
在现实生活中,有一类活动,由于它的特殊性,可将过程分成若干个互相联系的阶段,在它的每一阶段都需要作出决策,从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定,它依赖于当前面临的状态,又影响以后的发展。
所以如果一类活动过程可以分为若干个互相联系的阶段,在每一个阶段都需作出决策,每一个阶段都有若干个策略可供选择,一个阶段的策略确定以后,形成了本阶段的决策,常常影响到下一个阶段的决策,从而就完全确定了一个过程的活动路线,则称它为多阶段决策问题。
当各个阶段决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条活动路线。在多阶段决策问题中,决策依赖于当前状态,又随即引起状态的转移,一个决策序列就是在变化的状态中产生出来的,故有“动态”的含义,称这种解决多阶段决策最优化的过程为动态规划方法。
动态规划的解题步骤
- 确定状态转移公式,当前的状态是怎么由前面的状态变化而来的及其与之相关联的辅助的
DP数组(DP table)以及下标的含义。这一步往往也是最难的,这一步想清楚了,整个动态规划的问题基本上可以说就解决了一大半。一般来说,首先要确定中数组中元素代表的意义,然后在这个意义之下,确定状态是如何在DP数组的元素之间如何变化的。 - 初始化
DP数组。 - 根据题目条件确定遍历顺序,并实现状态转移公式。
再深入了解动态规划什么样的问题适合用动态规划
多阶段决策最优解模型
- 最优子结构
- 无后效性
- 重复子问题